2021中考数学考点专题训练——专题八：图形的相似(含答案)

这是一份2021中考数学考点专题训练——专题八：图形的相似(含答案)，共36页。
备战2021中考数学考点专题训练——专题八：图形的相似

1．如图，测量小玻璃管口径的量具ABC，AB的长为10cm，AC被分为60等份．如果小玻璃管口DE正好对着量具上20等份处（DE∥AB），那么小玻璃管口径DE是　 　cm．

2．小明想测量一棵树的高度，他发现树影子恰好落在地面和一斜坡上，如图，此时测得地面上的影长为8米，坡面上的影长为4米．已知斜坡的坡角为30°，同一时刻，一根长为1米、垂直于地面放置的标杆在地面上的影长为2米，则树的高度为　 　米．

3．如图，在矩形纸片ABCD中，AB＝6，BC＝10，点E在CD上，将△BCE沿BE折叠，点C恰落在边AD上的点F处；点G在AF上，将△ABG沿BG折叠，点A恰落在线段BF上的点H处，有下列结论：
①∠EBG＝45°；②△DEF∽△ABG；③S△ABG＝S△FGH；④AG+DF＝FG．
其中正确的是　 　．（把所有正确结论的序号都选上）

4．如图所示，已知点E在AC上，若点D在AB上，则满足条件　 　（只填一个条件），使△ADE与原△ABC相似．

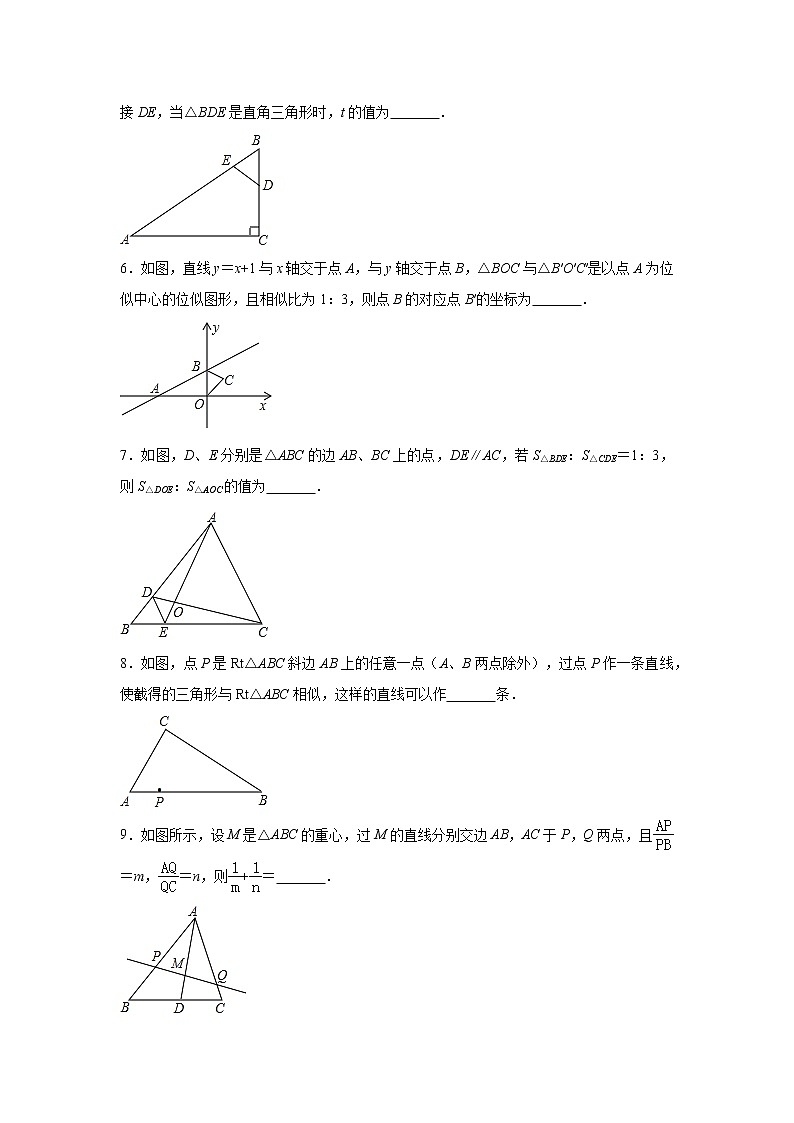
5．如图，△ABC中，∠ACB＝90°，AC＝8cm，BC＝6cm，D为BC的中点，若动点E以1cm/s的速度从A点出发，沿着A→B→A的方向运动，设E点的运动时间为t秒（0≤t＜15），连接DE，当△BDE是直角三角形时，t的值为　 　．

6．如图，直线y＝x+1与x轴交于点A，与y轴交于点B，△BOC与△B′O′C′是以点A为位似中心的位似图形，且相似比为1：3，则点B的对应点B′的坐标为　 　．

7．如图，D、E分别是△ABC的边AB、BC上的点，DE∥AC，若S△BDE：S△CDE＝1：3，则S△DOE：S△AOC的值为　 　．

8．如图，点P是Rt△ABC斜边AB上的任意一点（A、B两点除外），过点P作一条直线，使截得的三角形与Rt△ABC相似，这样的直线可以作　 　条．

9．如图所示，设M是△ABC的重心，过M的直线分别交边AB，AC于P，Q两点，且＝m，＝n，则+＝　 　．

10．如图，数学兴趣小组想测量电线杆AB的高度，他们发现电线杆的影子恰好落在土坡的坡面CD和地面BC上，量得CD＝4米，BC＝10米，CD与地面成30°角，且此时测得1米杆的影长为2米，则电线杆的高度约为　 　米（结果保留根号）

11．如图，点A1，A2，A3，A4，…，An在射线OA上，点B1，B2，B3，…，Bn﹣1在射线OB上，且A1B1∥A2B2∥A3B3∥…∥An﹣1Bn﹣1，A2B1∥A3B2∥A4B3∥…∥AnBn﹣1，△A1A2B1，△A2A3B2，…，△An﹣1AnBn﹣1为阴影三角形，若△A2B1B2，△A3B2B3的面积分别为1、4，则△A1A2B1的面积为　 　；面积小于2011的阴影三角形共有　 　个．

12．如图，一条4m宽的道路将矩形花坛分为一个直角三角形和一个直角梯形，根据图中数据，可知这条道路的占地面积为　 　m2．

13．如图，在直角坐标系中，△ABC的各顶点坐标为A（﹣1，1），B（2，3），C（0，3）．现以坐标原点为位似中心，作△A′B′C′，使△A′B′C′与△ABC的位似比为．则点A的对应点A′的坐标为　 　．

14．如图，在矩形纸片ABCD中，AB＝6，BC＝10，点E在CD上，将△BCE沿BE折叠，点C恰落在边AD上的点F处；点G在AF上，将△ABG沿BG折叠，点A恰落在线段BF上的点H处，有下列结论：
①∠EBG＝45°；②△DEF∽△ABG；③S△ABG＝S△FGH；④AG+DF＝FG．
其中正确的是　 　．（把所有正确结论的序号都选上）

15．如图，在Rt△ABC中，∠ACB＝90°，AB＝10，BC＝6，CD∥AB，∠ABC的平分线BD交AC于点E，DE＝　 　．

16．如图，已知点C为线段AB的中点，CD⊥AB且CD＝AB＝4，连接AD，BE⊥AB，AE是∠DAB的平分线，与DC相交于点F，EH⊥DC于点G，交AD于点H，则HG的长为　 　．

17．如图，△OAB与△OCD是以点O为位似中心的位似图形，点B在OD上，AE、CB分别是△OAB、△OCD的中线，则AE：CB的值为　 　

18．已知（如图①），矩形ABCD的一条边AD＝8，将矩形ABCD折叠，使得顶点B落在CD边上的P点处．连结AP、OP、OA，且△OCP与△PDA的面积比为1：4．再（如图②）擦去折痕AO、线段OP，连结BP．动点M在线段AP上（点M与点P、A不重合），动点N在线段AB的延长线上，且BN＝PM，连结MN交PB于点F，作ME⊥BP于点E．请求出动点M、N在移动的过程中，线段EF的长度是　 　

19．如图，在△ABC中，点D为AC上一点，且，过点D作DE∥BC交AB于点E，连接CE，过点D作DF∥CE交AB于点F．若AB＝15，则EF＝　 　．

20．如图，在△ABC中，DE∥BC，若AD＝1，DB＝2，则的值为　 　．

21．如图，在四边形ABCD中，∠DBC＝90°，∠ABD＝30°，∠ADB＝75°，AC与BD交于点E，若CE＝2AE＝4，则DC的长为　 　．

22．兴趣小组的同学要测量树的高度．在阳光下，一名同学测得一根长为1米的竹竿的影长为0.4米，同时另一名同学测量树的高度时，发现树的影子不全落在地面上，有一部分落在教学楼的第一级台阶上，测得此影子长为0.2米，一级台阶高为0.3米，如图所示，若此时落在地面上的影长为4.4米，则树高为　 　．

23．如图，小明把手臂水平向前伸直，手持小尺竖直，瞄准小尺的两端E、F，不断调整站立的位置，使在点D处恰好能看到铁塔的顶部B和底部A，设小明的手臂长l＝45cm，小尺长a＝15cm，点D到铁塔底部的距离AD＝42m，则铁塔的高度是　 　m．

24．如图，在△ABC中，∠ACB＝90°，点D，E分别在边AC，BC上，且∠CDE＝∠B，将△CDE沿DE折叠，点C恰好落在AB边上的点F处．若AC＝2BC，则的值为　 　．

25．如图，边长分别为4和8的两个正方形ABCD和CEFG并排放在一起，连结BD并延长交EG于点T，交FG于点P，则GT的长为　 　．

26．如图，边长12的正方形ABCD中，有一个小正方形EFGH，其中E、F、G分别在AB、BC、FD上．若BF＝3，则小正方形的边长为　 　．

27．如图，已知直线y＝﹣x+2与x轴交于点A，与y轴交于点B，在x轴上有一点C，使B、O、C三点构成的三角形与△AOB相似，则点C的坐标为　 　．

28．在平面直角坐标系中，点A（2，3），B（5，﹣2），以原点O为位似中心，位似比为1：2，把△ABO缩小，则点B的对应点B′的坐标是　 　．

29．如图，点G是△ABC的重心，GE∥BC，如果BC＝12，那么线段GE的长为　 　．

30．如图，已知在Rt△ABC中，AB＝AC＝3，在△ABC内作第一个内接正方形DEFG；然后取GF的中点P，连接PD、PE，在△PDE内作第二个内接正方形HIKJ；再取线段KJ的中点Q，在△QHI内作第三个内接正方形…依次进行下去，则第2014个内接正方形的边长为　 　．

31．如图：在平面直角坐标系中，直线y＝x+3与x轴、y轴分别交于A，B两点，直线y＝kx+8与直线AB相交于点D，与x轴相交于点C，过D作DE⊥x轴于点E（1，0），点P（t，0）为x轴上一动点．若点T 为直线DE上一动点，当以O，B，T为顶点的三角形与以O，B，P为顶点的三角形相似时，则相应的点T（t＜0）的坐标为　 　．

32．如图，△AOB是直角三角形，∠AOB＝90°，OB＝2OA，点A在反比例函数y＝的图象上．若点B在反比例函数y＝的图象上，则k的值为　 　．

33．如图，在平面直角坐标系中，点A、B的坐标分别为（4，0）、（0，2），点C为线段AB上任意一点（不与点A、B重合）．CD⊥OA于点D，点E在DC的延长线上，EF⊥y轴于点F，若点C为DE中点，则四边形ODEF的周长为　 　．

34．如图，在Rt△ABC中，∠ACB＝90°，AB＝4，点D，E分别在边AB，AC上，且DB＝2AD，AE＝3EC，连接BE，CD，相交于点O，则△ABO面积最大值为　 　．

35．如图，小明周末晚上陪父母在锦江绿道上散步，他由灯下A处前进4米到达B处时，测得影子BC长为1米，已知小明身高1.6米，他若继续往前走4米到达D处，此时影子DE长为　 　米．





























备战2021中考数学考点专题训练——专题八：图形的相似参考答案
1．如图，测量小玻璃管口径的量具ABC，AB的长为10cm，AC被分为60等份．如果小玻璃管口DE正好对着量具上20等份处（DE∥AB），那么小玻璃管口径DE是　 　cm．

【答案】解：∵DE∥AB，
∴△CDE∽△CAB．
∴DE：AB＝CD：AC．
∴40：60＝DE：10．
∴DE＝cm．
∴小玻璃管口径DE是cm．
故答案为：．
2．小明想测量一棵树的高度，他发现树影子恰好落在地面和一斜坡上，如图，此时测得地面上的影长为8米，坡面上的影长为4米．已知斜坡的坡角为30°，同一时刻，一根长为1米、垂直于地面放置的标杆在地面上的影长为2米，则树的高度为　 　米．

【答案】解：延长AC交BF延长线于D点，
则∠CFE＝30°，作CE⊥BD于E，
在Rt△CFE中，∠CFE＝30°，CF＝4m，
∴CE＝2（米），EF＝4cos30°＝2（米），
在Rt△CED中，
∵同一时刻，一根长为1米、垂直于地面放置的标杆在地面上的影长为2米，CE＝2（米），CE：DE＝1：2，
∴DE＝4（米），
∴BD＝BF+EF+ED＝12+2（米）
在Rt△ABD中，AB＝BD＝（12+2）＝（+6）（米）．
故答案为：（+6）．

3．如图，在矩形纸片ABCD中，AB＝6，BC＝10，点E在CD上，将△BCE沿BE折叠，点C恰落在边AD上的点F处；点G在AF上，将△ABG沿BG折叠，点A恰落在线段BF上的点H处，有下列结论：
①∠EBG＝45°；②△DEF∽△ABG；③S△ABG＝S△FGH；④AG+DF＝FG．
其中正确的是　 　．（把所有正确结论的序号都选上）

【答案】解：∵△BCE沿BE折叠，点C恰落在边AD上的点F处，
∴∠1＝∠2，CE＝FE，BF＝BC＝10，
在Rt△ABF中，∵AB＝6，BF＝10，
∴AF＝＝8，
∴DF＝AD﹣AF＝10﹣8＝2，
设EF＝x，则CE＝x，DE＝CD﹣CE＝6﹣x，
在Rt△DEF中，∵DE2+DF2＝EF2，
∴（6﹣x）2+22＝x2，解得x＝，
∴ED＝，
∵△ABG沿BG折叠，点A恰落在线段BF上的点H处，
∴∠3＝∠4，BH＝BA＝6，AG＝HG，
∴∠2+∠3＝∠ABC＝45°，所以①正确；
HF＝BF﹣BH＝10﹣6＝4，
设AG＝y，则GH＝y，GF＝8﹣y，
在Rt△HGF中，∵GH2+HF2＝GF2，
∴y2+42＝（8﹣y）2，解得y＝3，
∴AG＝GH＝3，GF＝5，
∵∠A＝∠D，＝＝，＝，
∴≠，
∴△ABG与△DEF不相似，所以②错误；
∵S△ABG＝•6•3＝9，S△FGH＝•GH•HF＝×3×4＝6，
∴S△ABG＝S△FGH，所以③正确；
∵AG+DF＝3+2＝5，而GF＝5，
∴AG+DF＝GF，所以④正确．
故答案为①③④．

4．如图所示，已知点E在AC上，若点D在AB上，则满足条件　 　（只填一个条件），使△ADE与原△ABC相似．

【答案】解：已知点E在AC上，若点D在AB上，则满足条件∠B＝∠AED（只填一个条件），使△ADE与原△ABC相似，
故答案为：∠B＝∠AED．
5．如图，△ABC中，∠ACB＝90°，AC＝8cm，BC＝6cm，D为BC的中点，若动点E以1cm/s的速度从A点出发，沿着A→B→A的方向运动，设E点的运动时间为t秒（0≤t＜15），连接DE，当△BDE是直角三角形时，t的值为　 　．

【答案】解：当DE⊥AB于点E，
设t秒时，E点没有到达B点前，∠BED＝90°，
∵∠B＝∠B，∠ACB＝∠BED＝90°，
∴△BED∽△BCA，
∴＝，
∵∠ACB＝90°，AC＝8cm，BC＝6cm，D为BC的中点，
∴AB＝10cm，BD＝3cm，
∴＝，
解得：t＝8.2，
设t秒时，当E点到达B点后，∠BED＝90°，
∵∠B＝∠B，∠ACB＝∠BED＝90°，
∴△BED∽△BCA，
∴＝，
∵∠ACB＝90°，AC＝8cm，BC＝6cm，D为BC的中点，
∴AB＝10cm，BD＝3cm，
∴＝，
解得：t＝11.8，
当DE⊥CB于DE，
设t秒时，∠BDE＝90°，
∵DE∥AC，
∴△BED∽△BAC，
∴＝＝，
∵∠ACB＝90°，AC＝8cm，BC＝6cm，D为BC的中点，
∴AB＝10cm，BD＝3cm，
∴＝
解得：t＝5，
综上所述：t的值为5s或8.2s或11.8s．
故答案为：5s或8.2s或11.8s．
6．如图，直线y＝x+1与x轴交于点A，与y轴交于点B，△BOC与△B′O′C′是以点A为位似中心的位似图形，且相似比为1：3，则点B的对应点B′的坐标为　 　．

【答案】解：∵直线y＝x+1与x轴交于点A，与y轴交于点B，
令x＝0可得y＝1；
令y＝0可得x＝﹣1，
∴点A和点B的坐标分别为（﹣1，0）；（0，1），
∵△BOC与△B′O′C′是以点A为位似中心的位似图形，且相似比为1：3，
∴＝＝，
∴O′B′＝3，AO′＝3，
∴B′的坐标为（﹣4，﹣3）或（2，3）．
故答案为：（﹣4，﹣3）或（2，3）．
7．如图，D、E分别是△ABC的边AB、BC上的点，DE∥AC，若S△BDE：S△CDE＝1：3，则S△DOE：S△AOC的值为　 　．

【答案】解：∵S△BDE：S△CDE＝1：3，
∴BE：EC＝1：3；
∴BE：BC＝1：4；
∵DE∥AC，
∴△BDE∽△BAC，△DOE∽△AOC，
∴＝，
∴S△DOE：S△AOC＝（）2＝；
故答案为：1：16．
8．如图，点P是Rt△ABC斜边AB上的任意一点（A、B两点除外），过点P作一条直线，使截得的三角形与Rt△ABC相似，这样的直线可以作　 　条．

【答案】解：过点P可作PE∥BC或PE∥AC，可得相似三角形；
过点P还可作PE⊥AB，可得：∠EPA＝∠C＝90°，∠A＝∠A，
∴△APE∽△ACB；
所以共有3条．

9．如图所示，设M是△ABC的重心，过M的直线分别交边AB，AC于P，Q两点，且＝m，＝n，则+＝　 　．

【答案】解：分别过点B，C作BE∥AD，CF∥AD，交PQ于点E，F，则BE∥AD∥CF，
∵点D是BC的中点，
∴MD是梯形的中位线，
∴BE+CF＝2MD，
∴+＝＝+＝＝＝1．

10．如图，数学兴趣小组想测量电线杆AB的高度，他们发现电线杆的影子恰好落在土坡的坡面CD和地面BC上，量得CD＝4米，BC＝10米，CD与地面成30°角，且此时测得1米杆的影长为2米，则电线杆的高度约为　 　米（结果保留根号）

【答案】解：如图，过D作DE⊥BC的延长线于E，连接AD并延长交BC的延长线于F，
∵CD＝4米，CD与地面成30°角，
∴DE＝CD＝×4＝2米，
根据勾股定理得，CE＝＝＝2米，
∵1米杆的影长为2米，
∴＝，
∴EF＝2DE＝2×2＝4米，
∴BF＝BC+CE+EF＝10+2+4＝（14+2）米，
∴＝，
∴AB＝（14+2）＝（7+）米．
故答案为：（7+）．

11．如图，点A1，A2，A3，A4，…，An在射线OA上，点B1，B2，B3，…，Bn﹣1在射线OB上，且A1B1∥A2B2∥A3B3∥…∥An﹣1Bn﹣1，A2B1∥A3B2∥A4B3∥…∥AnBn﹣1，△A1A2B1，△A2A3B2，…，△An﹣1AnBn﹣1为阴影三角形，若△A2B1B2，△A3B2B3的面积分别为1、4，则△A1A2B1的面积为　 　；面积小于2011的阴影三角形共有　 　个．

【答案】解：由题意得，△A2B1B2∽△A3B2B3，
∴＝＝，＝＝，
又∵A1B1∥A2B2∥A3B3，
∴＝＝＝，＝＝，
∴OA1＝A1A2，B1B2＝B2B3
继而可得出规律：A1A2＝A2A3＝A3A4…；B1B2＝B2B3＝B3B4…
又△A2B1B2，△A3B2B3的面积分别为1、4，
∴S△A1B1A2＝，S△A2B2A3＝2，
继而可推出S△A3B3A4＝8，S△A4B4A5＝32，S△A5B5A6＝128，S△A6B6A7＝512，S△A7B7A8＝2048，
故可得小于2011的阴影三角形的有：△A1B1A2，△A2B2A3，△A3B3A4，△A4B4A5，△A5B5A6，△A6B6A7，共6个．
故答案是：；6．
12．如图，一条4m宽的道路将矩形花坛分为一个直角三角形和一个直角梯形，根据图中数据，可知这条道路的占地面积为　 　m2．

【答案】解：如图，作DE⊥AC于点E，
∵道路的宽为4m，
∴DE＝4米，
∵AE＝3m
∵∠DAE+∠BAE＝90°，∠DAE+∠ADE＝90°，
∴∠BAE＝∠ADE
∴△DAE∽△ACB
∴＝
即：
解得：AB＝16（m），
∴道路的面积为AD×AB＝5×16＝80（m2）．

13．如图，在直角坐标系中，△ABC的各顶点坐标为A（﹣1，1），B（2，3），C（0，3）．现以坐标原点为位似中心，作△A′B′C′，使△A′B′C′与△ABC的位似比为．则点A的对应点A′的坐标为　 　．

【答案】解：∵在△A′B′C′中，它的对应点的坐标是（kx，ky）或（﹣kx，﹣ky）
∴A'的坐标为：（﹣，）或（，﹣）．
故答案为：（﹣，）或（，﹣）．
14．如图，在矩形纸片ABCD中，AB＝6，BC＝10，点E在CD上，将△BCE沿BE折叠，点C恰落在边AD上的点F处；点G在AF上，将△ABG沿BG折叠，点A恰落在线段BF上的点H处，有下列结论：
①∠EBG＝45°；②△DEF∽△ABG；③S△ABG＝S△FGH；④AG+DF＝FG．
其中正确的是　 　．（把所有正确结论的序号都选上）

【答案】解：∵△BCE沿BE折叠，点C恰落在边AD上的点F处，
∴∠1＝∠2，CE＝FE，BF＝BC＝10，
在Rt△ABF中，∵AB＝6，BF＝10，
∴AF＝＝8，
∴DF＝AD﹣AF＝10﹣8＝2，
设EF＝x，则CE＝x，DE＝CD﹣CE＝6﹣x，
在Rt△DEF中，∵DE2+DF2＝EF2，
∴（6﹣x）2+22＝x2，解得x＝，
∴ED＝，
∵△ABG沿BG折叠，点A恰落在线段BF上的点H处，
∴∠3＝∠4，BH＝BA＝6，AG＝HG，
∴∠2+∠3＝∠ABC＝45°，所以①正确；
HF＝BF﹣BH＝10﹣6＝4，
设AG＝y，则GH＝y，GF＝8﹣y，
在Rt△HGF中，∵GH2+HF2＝GF2，
∴y2+42＝（8﹣y）2，解得y＝3，
∴AG＝GH＝3，GF＝5，
∵∠A＝∠D，＝＝，＝，
∴≠，
∴△ABG与△DEF不相似，所以②错误；
∵S△ABG＝•6•3＝9，S△FGH＝•GH•HF＝×3×4＝6，
∴S△ABG＝S△FGH，所以③正确；
∵AG+DF＝3+2＝5，而GF＝5，
∴AG+DF＝GF，所以④正确．
故答案为①③④．

15．如图，在Rt△ABC中，∠ACB＝90°，AB＝10，BC＝6，CD∥AB，∠ABC的平分线BD交AC于点E，DE＝　 　．

【答案】解：∵∠ACB＝90°，AB＝10，BC＝6，
∴AC＝8，
∵BD平分∠ABC，
∴∠ABE＝∠CBD，
∵CD∥AB，
∴∠D＝∠ABD，
∴∠D＝∠CBE，
∴CD＝BC＝6，
∴△AEB∽△CED，
∴，
∴CE＝AC＝×8＝3，
BE＝，
DE＝BE＝×＝，
故答案为．

16．如图，已知点C为线段AB的中点，CD⊥AB且CD＝AB＝4，连接AD，BE⊥AB，AE是∠DAB的平分线，与DC相交于点F，EH⊥DC于点G，交AD于点H，则HG的长为　 　．

【答案】解：∵AB＝CD＝4，C为线段AB的中点，
∴BC＝AC＝2，
∴AD＝2，
∵EH⊥DC，CD⊥AB，BE⊥AB，
∴EH∥AC，四边形BCGE为矩形，
∴∠HEA＝∠EAB，BC＝GE＝2，
又∵AE是∠DAB的平分线，
∴∠EAB＝∠DAE，
∴∠DAE＝∠HEA，
∴HA＝HE，
设GH＝x，
则HA＝HE＝HG+GE＝2+x，
∵EH∥AC，
∴△DHG∽△DAC，
∴＝，即＝，
解得：x＝3﹣，
即HG＝3﹣，
故答案为：3﹣．
17．如图，△OAB与△OCD是以点O为位似中心的位似图形，点B在OD上，AE、CB分别是△OAB、△OCD的中线，则AE：CB的值为　 　

【答案】解：∵，△OAB与△OCD是以点O为位似中心的位似图形，
又∵AE、CB分别是△OAB、△OCD的中线，
∴相似比是，
∴AE：CB＝1：2，
故答案为：1：2
18．已知（如图①），矩形ABCD的一条边AD＝8，将矩形ABCD折叠，使得顶点B落在CD边上的P点处．连结AP、OP、OA，且△OCP与△PDA的面积比为1：4．再（如图②）擦去折痕AO、线段OP，连结BP．动点M在线段AP上（点M与点P、A不重合），动点N在线段AB的延长线上，且BN＝PM，连结MN交PB于点F，作ME⊥BP于点E．请求出动点M、N在移动的过程中，线段EF的长度是　 　

【答案】解：由折叠的性质可知，∠APO＝∠B＝90°，
∴∠APD+∠CPO＝90°，又∠APD+∠DAP＝90°，
∴∠DAP＝∠CPO，又∠D＝∠C＝90°，
∴△OCP∽△PDA；
∵△OCP∽△PDA，面积比为1：4，
∴，
∴CP＝4，
∴BP＝＝＝4
作MH∥AB交PB于H，

∴∠PHM＝∠PBA，
∵AP＝AB，
∴∠APB＝∠PBA，
∴∠APB＝∠PHM，
∴MP＝MH，又BN＝PM，
∴MH＝BN，
又∵MH∥AB，
∴BF＝FH，
∵MP＝MH，ME⊥BP，
∴PE＝EH，
∴PB＝2EF，
∴EF＝PB＝2，
故答案为2．
19．如图，在△ABC中，点D为AC上一点，且，过点D作DE∥BC交AB于点E，连接CE，过点D作DF∥CE交AB于点F．若AB＝15，则EF＝　 　．

【答案】解：∵DE∥BC，
∴＝，
∵＝，
∴＝，即＝，
∵AB＝15，
∴AE＝10，
∵DF∥CE，
∴＝，即＝，
解得：AF＝，
则EF＝AE﹣AF＝10﹣＝，
故答案为：
20．如图，在△ABC中，DE∥BC，若AD＝1，DB＝2，则的值为　 　．

【答案】解：∵DE∥BC，
∴＝，
∵AD＝1，BD＝2，
∴AB＝3，
∴＝，
故答案为：．
21．如图，在四边形ABCD中，∠DBC＝90°，∠ABD＝30°，∠ADB＝75°，AC与BD交于点E，若CE＝2AE＝4，则DC的长为　 　．

【答案】解：过A点作A⊥BD于F，
∵∠DBC＝90°，
∴AF∥BC，
∵CE＝2AE，
∴AF＝BC，
∵∠ABD＝30°，
∴AF＝AB，
∴BC＝AB，
∵∠ABD＝30°，∠ADB＝75°，
∴∠BAD＝75°，∠ACB＝30°，
∴∠ADB＝∠BAD，
∴BD＝AB，
∴BC＝BD，
∵CE＝4，
在Rt△CBE中，BC＝CE＝6，
在Rt△CBD中，CD＝BC＝6．
故答案为：6．

22．兴趣小组的同学要测量树的高度．在阳光下，一名同学测得一根长为1米的竹竿的影长为0.4米，同时另一名同学测量树的高度时，发现树的影子不全落在地面上，有一部分落在教学楼的第一级台阶上，测得此影子长为0.2米，一级台阶高为0.3米，如图所示，若此时落在地面上的影长为4.4米，则树高为　 　．

【答案】解：根据题意可构造相似三角形模型如图，
其中AB为树高，EF为树影在第一级台阶上的影长，BD为树影在地上部分的长，ED的长为台阶高，并且由光沿直线传播的性质可知BC即为树影在地上的全长；
延长FE交AB于G，则Rt△ABC∽Rt△AGF，
∴AG：GF＝AB：BC＝物高：影长＝1：0.4
∴GF＝0.4AG
又∵GF＝GE+EF，BD＝GE，GE＝4.4m，EF＝0.2m，
∴GF＝4.6
∴AG＝11.5
∴AB＝AG+GB＝11.8，即树高为11.8米．

23．如图，小明把手臂水平向前伸直，手持小尺竖直，瞄准小尺的两端E、F，不断调整站立的位置，使在点D处恰好能看到铁塔的顶部B和底部A，设小明的手臂长l＝45cm，小尺长a＝15cm，点D到铁塔底部的距离AD＝42m，则铁塔的高度是　 　m．

【答案】解：作CH⊥AB于H，交EF于P，如图，则CH＝DA＝42m，CP＝45cm＝0.45m，EF＝15cm＝0.15m，
∵EF∥AB，
∴△CEF∽△CBA，
∴＝，即＝，
∴AB＝14（m），
即铁塔的高度为14m．
故答案为14．

24．如图，在△ABC中，∠ACB＝90°，点D，E分别在边AC，BC上，且∠CDE＝∠B，将△CDE沿DE折叠，点C恰好落在AB边上的点F处．若AC＝2BC，则的值为　 　．

【答案】解：如图，设DE交CF于O．设OD＝a．

由翻折可知：DC＝DF，EC＝EF，
∴DE垂直平分线段CF，
∴∠DOC＝90°，OC＝OF，
∵∠CDE＝∠B，
∴tan∠CDO＝tan∠B，
∴＝＝2，
∴OC＝OF＝2a，CF＝4a，
∵∠ECO+∠DCO＝90°，∠DCO+∠CDO＝90°，
∴∠ECO＝∠CDO，
∴tan∠ECO＝2＝，
∴OE＝4a，DE＝5a，
∴＝＝，
故答案为．
25．如图，边长分别为4和8的两个正方形ABCD和CEFG并排放在一起，连结BD并延长交EG于点T，交FG于点P，则GT的长为　 　．

【答案】解：∵BD、GE分别是正方形ABCD，正方形CEFG的对角线，
∴∠ADB＝∠CGE＝45°，
∴∠GDT＝180°﹣90°﹣45°＝45°，
∴∠DTG＝180°﹣∠GDT﹣∠CGE＝180°﹣45°﹣45°＝90°，
∴△DGT是等腰直角三角形，
∵两正方形的边长分别为4，8，
∴DG＝8﹣4＝4，
∴GT＝×4＝2．
故答案为：2．
26．如图，边长12的正方形ABCD中，有一个小正方形EFGH，其中E、F、G分别在AB、BC、FD上．若BF＝3，则小正方形的边长为　 　．

【答案】解：在△BEF与△CFD中
∵∠1+∠2＝∠2+∠3＝90°，
∴∠1＝∠3，
∵∠B＝∠C＝90°，
∴△BEF∽△CFD，
∵BF＝3，BC＝12，
∴CF＝BC﹣BF＝12﹣3＝9，
又∵DF＝＝＝15，
∴＝，即＝，
∴EF＝，
故答案为：．

27．如图，已知直线y＝﹣x+2与x轴交于点A，与y轴交于点B，在x轴上有一点C，使B、O、C三点构成的三角形与△AOB相似，则点C的坐标为　 　．

【答案】解：∵直线y＝﹣x+2与x轴交于点A，与y轴交于点B，
∴A（4，0），B（0，2）．
当△AOB∽△BOC时，
＝，即＝，解得OC＝1，
∴C（﹣1，0），（1，0）．
当△AOB∽△COB时，点C与A重合，C（4，0）或（﹣4，0）
综上所述，点C的坐标为（﹣1，0）或（1，0）或（4，0）或（﹣4，0）．
故答案为：（﹣1，0）或（1，0）或（﹣4，0）或（4，0）．
28．在平面直角坐标系中，点A（2，3），B（5，﹣2），以原点O为位似中心，位似比为1：2，把△ABO缩小，则点B的对应点B′的坐标是　 　．

【答案】解：∵以原点O为位似中心，位似比为1：2，把△ABO缩小，B（5，﹣2），
∴点B的对应点B′的坐标是：（，﹣1）或（﹣，1）．
故答案为：（，﹣1）或（﹣，1）．
29．如图，点G是△ABC的重心，GE∥BC，如果BC＝12，那么线段GE的长为　 　．

【答案】解：∵点G是△ABC的重心，
∴AD为中线，AG＝2GD，
∴AD＝CD＝BC＝6，
∵GE∥BC，
∴△AGE∽△ADC，
∴＝，即＝，
∴GE＝4．
故答案为4．
30．如图，已知在Rt△ABC中，AB＝AC＝3，在△ABC内作第一个内接正方形DEFG；然后取GF的中点P，连接PD、PE，在△PDE内作第二个内接正方形HIKJ；再取线段KJ的中点Q，在△QHI内作第三个内接正方形…依次进行下去，则第2014个内接正方形的边长为　 　．

【答案】解：∵在Rt△ABC中，AB＝AC＝，
∴∠B＝∠C＝45°，BC＝，
∵在△ABC内作第一个内接正方形DEFG；
∴EF＝EC＝DG＝BD，
∴DE＝BC
∴DE＝2，
∵取GF的中点P，连接PD、PE，在△PDE内作第二个内接正方形HIKJ；再取线段KJ的中点Q，在△QHI内作第三个内接正方形…依次进行下去，
∴，
∴EI＝KI＝HI，
∵DH＝EI，
∴HI＝DE＝，
则第n个内接正方形的边长为：2×，
∴则第2014个内接正方形的边长为2×＝2×＝．
故答案为：．
31．如图：在平面直角坐标系中，直线y＝x+3与x轴、y轴分别交于A，B两点，直线y＝kx+8与直线AB相交于点D，与x轴相交于点C，过D作DE⊥x轴于点E（1，0），点P（t，0）为x轴上一动点．若点T 为直线DE上一动点，当以O，B，T为顶点的三角形与以O，B，P为顶点的三角形相似时，则相应的点T（t＜0）的坐标为　 　．

【答案】解：根据题意知点B的坐标为（0，3），
如图1，BT＝1，OB＝3，

①当△BOP∽△OBT或△POB∽△OBT时，∠POB＝∠TBO＝90°，
∴此时点T的坐标为（1，3）；

②当△BOP∽△BOT或△POB∽△BOT时，∠BOP＝∠BOT＝90°，
∴点T的坐标为（1，0）；

③如图2，设点T坐标为（1，a），过点B作BF⊥DE于F，

∴∠BFT＝∠TEO＝90°，
∴∠BTF+∠TBF＝90°，
当△BOP∽△BTO时，∠BTO＝∠BOP＝90°，
∴∠BTF+∠OTE＝90°，
∴∠TBF＝∠OTE，
∴△BTF∽△TOE，
∴，即＝＝，
解得a＝或a＝，
∴点T的坐标为（1，）或（1，），
综上点T的坐标为（1，3）或（1，0）或（1，）或（1，）．
32．如图，△AOB是直角三角形，∠AOB＝90°，OB＝2OA，点A在反比例函数y＝的图象上．若点B在反比例函数y＝的图象上，则k的值为　 　．

【答案】解：过点A，B作AC⊥x轴，BD⊥x轴，分别于C，D．

设点A的坐标是（m，n），则AC＝n，OC＝m．
∵∠AOB＝90°，
∴∠AOC+∠BOD＝90°．
∵∠DBO+∠BOD＝90°，
∴∠DBO＝∠AOC．
∵∠BDO＝∠ACO＝90°，
∴△BDO∽△OCA．
∴．
∵OB＝2OA，
∴BD＝2m，OD＝2n．
因为点A在反比例函数y＝的图象上，
∴mn＝1．
∵点B在反比例函数y＝的图象上，
∴B点的坐标是（﹣2n，2m）．
∴k＝﹣2n•2m＝﹣4mn＝﹣4．
故答案为：﹣4．
33．如图，在平面直角坐标系中，点A、B的坐标分别为（4，0）、（0，2），点C为线段AB上任意一点（不与点A、B重合）．CD⊥OA于点D，点E在DC的延长线上，EF⊥y轴于点F，若点C为DE中点，则四边形ODEF的周长为　 　．

【答案】解：设直线AB的解析式为y＝kx+b，
将点A（4，0）、点B（0，2）代入y＝kx+b中，
得：，
解得：．
∴直线AB的解析式为y＝﹣x+2．
设点C的坐标为（m，﹣m+2）（0＜m＜4），则点E的坐标为（m，﹣m+4），
∴OD＝EF＝m，CD＝2﹣m，DE＝4﹣m，
∵ED⊥OA，EF⊥y轴，BO⊥OA，
∴∠O＝∠F＝∠ODE＝90°，
∴四边形ODEF为矩形．
∴C矩形ODEF＝2×（OD+DE）＝2×（m+4﹣m）＝8．
故答案为：8．
34．如图，在Rt△ABC中，∠ACB＝90°，AB＝4，点D，E分别在边AB，AC上，且DB＝2AD，AE＝3EC，连接BE，CD，相交于点O，则△ABO面积最大值为　 　．

【答案】解：如图，过点D作DF∥AE，

则＝＝，
∵＝，
∴DF＝2EC，
∴DO＝2OC，
∴DO＝DC，
∴S△ADO＝S△ADC，S△BDO＝S△BDC，
∴S△ABO＝S△ABC，
∵∠ACB＝90°，
∴C在以AB为直径的圆上，设圆心为G，
当CG⊥AB时，△ABC的面积最大为：4×2＝4，
此时△ABO的面积最大为：×4＝．
故答案为：．
35．如图，小明周末晚上陪父母在锦江绿道上散步，他由灯下A处前进4米到达B处时，测得影子BC长为1米，已知小明身高1.6米，他若继续往前走4米到达D处，此时影子DE长为　 　米．

【答案】解：由FB∥AP可得，△CBF∽△CAP，
∴，即，
解得AP＝8，
由GD∥AP可得，△EDG∽△EAP，
∴，即，
解得ED＝2，
故答案为：2．