

2020-2021学年四川省成都市温江区六年级(上)期末数学试卷
展开2020-2021学年四川省成都市温江区六年级(上)期末数学试卷
一、选择题(本大题共20小题,每小题1.5分,共30分)
1.(1.5分)如图,梯形部分占整幅图的多少?用百分数表示为( )
A.48% B.54% C.27% D.13.5%
2.(1.5分)10名运动员参加比赛,如果每2人握1次手,一共要握手( )次。
A.45 B.55 C.90 D.100
3.(1.5分)工厂质检员检查一批零件,合格的为a件,不合格的为b件,这批零件的合格率是( )
A.×100% B.×100% C.×100% D.×100%
4.(1.5分)一根绳子分成两段,第一段长米,第二段占全长的,比较两段绳子的长( )
A.第一段长 B.第二段长 C.一样长 D.无法比较
5.(1.5分)银行两年期的存款年利率是2.10%。爸爸把8000元钱存入银行,存定期两年,到期后爸爸可得本息一共多少元?下面列式正确的是( )
A.8000×2.10%×2 B.8000×(1+2.10%)×2
C.8000×(1+2.10%×2) D.8000×(1+2.10%)
6.(1.5分)一个减法算式中,减数是差的,被减数与差的最简整数比是( )
A.3:2 B.2:3 C.5:2 D.5:3
7.(1.5分)一堆货物有4吨,第一次运走了总质量的,第二次运走了吨,算式“4×﹣”解决的问题是( )
A.两次共运走了多少吨
B.第一次运走了多少吨
C.两次后还剩下多少吨
D.第一次比第二次多运了多少吨
8.(1.5分)一件商品原来在甲商场和乙商场的售价相同.甲商场先降价10%,再涨价10%;乙商场先涨价10%,再降价10%。这件商品现在在两个商场的售价相比( )
A.甲商场贵 B.乙商场贵 C.售价一样 D.无法确定
9.(1.5分)一辆汽车从甲地到乙地,去时用8小时,返回用10小时,返回的速度相当于去时速度的( )
A.20% B.25% C.80% D.125%
10.(1.5分)甲、乙、丙三人分水果,方案一是按3:4:5分配,方案二是按2:3:4分配,那么按这两种方案分配,乙分得的水果数量( )
A.一样多 B.第一种方案分得多
C.第二种方案分得多 D.无法确定
11.(1.5分)一个立体图形,从上面看到的形状是,从正面看到的形状是,从左面看到的形状是.要搭成这个立体图形至少需要( )个小正方体.
A.4 B.5 C.6 D.7
12.(1.5分)如图所示,在房子外的屋檐E处有一台监视器,房子前面有一面落地的广告牌BD,那么监视器看不到的区域是( )
A.三角形AFD B.三角形BFD C.三角形ABD D.四边形BDEC
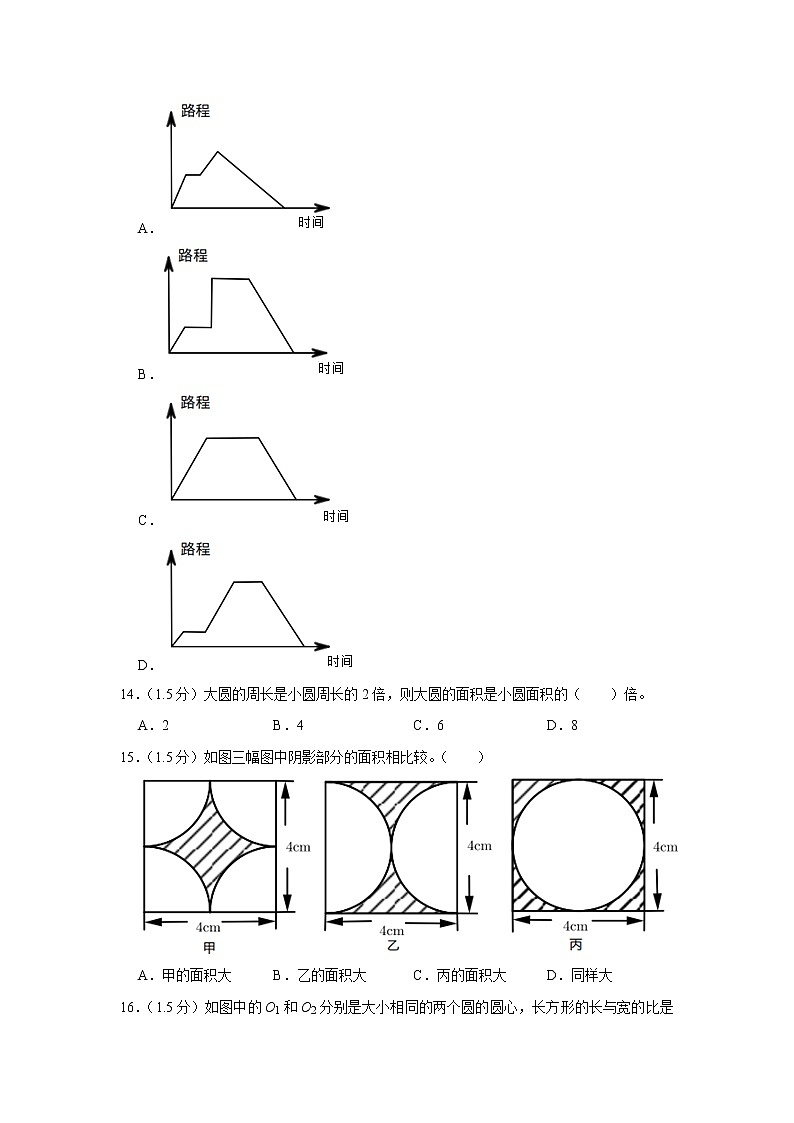
13.(1.5分)淘气去超市买东西,在路上遇到同学交谈了一会,然后去超市买了一些学习用品后回家,下面( )图比较准确地反映了淘气的活动。
A.
B.
C.
D.
14.(1.5分)大圆的周长是小圆周长的2倍,则大圆的面积是小圆面积的( )倍。
A.2 B.4 C.6 D.8
15.(1.5分)如图三幅图中阴影部分的面积相比较。( )
A.甲的面积大 B.乙的面积大 C.丙的面积大 D.同样大
16.(1.5分)如图中的O1和O2分别是大小相同的两个圆的圆心,长方形的长与宽的比是( )
A.2:1 B.3:2 C.3:1 D.4:3
17.(1.5分)如图,大圆内有3个大小不等的小圆,这四个圆的圆心都在同一直线上,若大圆的直径是5厘米,则三个小圆的周长之和是( )厘米。
A.7.85 B.15.7 C.31.4 D.78.5
18.(1.5分)如图1,把圆沿半径平均分成若干等份,就能得到一个近似的长方形.如果分的份数越多,拼成的图形就越接近长方形。
如图2中的长方形OABC就是由圆O用这样的方法得到的,则阴影部分的面积与圆面积的最简整数比是( )
A.4:3 B.3:5 C.3:4 D.无法确定
19.(1.5分)把一根铁丝围成一个圆,半径正好是a分米,如果把这根铁丝围成一个正方形,它的边长是( )分米。
A.1.57a B.3.14a C.6.28a D.3.14a2
20.(1.5分)如图甲是用无人机从高空拍摄的笑笑家的图片。地面上有①、②、③、④四个观察点,笑笑站在地面上的( )号位置看到的样子如图乙所示。
A.① B.② C.③ D.④
二、计算(本大题共4小题,共23分)
21.(8分)直接写出得数。
(1)1﹣27%=
(2)+25%=
(3)15×30%=
(4)45÷45%=
(5)﹣=
(6)+=
(7)1÷×=
(8)3÷÷=
22.(9分)先化简比,再求比值。
(1)0.8:
(2)0.07:4.2
(3):
23.(12分)脱式计算。
(1)7÷+÷7
(2)3×8×(+75%)
(3)(﹣×)÷
(4)0.8×7.7﹣80%+3.3×
24.(4分)解方程。
(1)x﹣25%x=
(2)x+=4
三、操作题(本大题共2小题,每小题6分,共12分)
25.(6分)某学校六年级科学考试结果以等级呈现,分A、B、C、D四个等级,在一次模拟考试后,随机抽取部分学生的科学成绩进行调查统计,绘制成如下两幅不完整的统计图。
(1)这次调查共抽取了 名学生的科学成绩。
(2)B等的学生人数占抽样学生人数的 。(填百分数)
(3)请把条形统计图补充完整。
(4)如果该校六年级有800名学生,这次模拟考试大约有 名学生的科学成绩为D等。
26.(6分)如图所示,O为圆心,OACB为梯形。求阴影部分的周长与面积。(单位:cm)
四、解决问题(本大题共5小题,每小题5分,共25分)
27.(5分)我国大约有60个城市,其中约有的城市供水不足,在这些供水不足的城市中,约有城市严重缺水,全国严重缺水的城市大约有多少个?
28.(5分)淘气家九月份用水14吨,九月份比八月份节约了,淘气家八月份用水多少吨?(用方程解答)
29.(5分)一辆汽车车轮半径为0.4米,车轮每分钟转动500圈,这辆汽车1小时可以行驶多少千米?
30.(5分)一个圆形花坛,直径为20米,在花坛中央有一个半径为2米的圆形喷水池,其余部分按3:5的比例种植草和花,种花的面积是多少平方米?
31.(5分)某项工程由三个工程队共同完成。根据合同,各工程队需完成的工程量如下:甲工程队完成总工程的30%,余下的任务由乙、丙两个工程队按3:4进行分配。当甲工程队完成4000米时,甲正好完成工程总长的。求丙工程队应完成的工程量是多少米?
五、附加题.填空题。(本大题共5小题,共10分)
32.(2分)一件商品按100元定价后,打九折出售,仍能获得20%的利润,这件商品的进价是 元。
33.(2分)一个圆的周长、直径、半径相加的和是27.84厘米,这个圆的面积是 平方厘米。
34.(2分)图中,两个正方形中阴影部分的面积比是3:1,空白部分甲和乙的面积比是 .
35.(2分)如图所示,O为大小两个圆的圆心,阴影部分的面积是8平方厘米,圆环的面积是 平方厘米。
36.(2分)一个长方形沿虚线折叠后得到一个多边形(如图所示),这个多边形的面积是原长方形面积的。如果多边形中涂色部分的总面积是2平方厘米,那么原长方形的面积是 平方厘米。
六、解答题本大题共2小题,每小题5分,共10分)
37.(5分)加工一批零件,原计划每天加工15个,若干天可以完成.当完成加工任务的时,采用新技术,效率提高20%.结果,完成任务的时间提前10天,这批零件共有几个?
38.(5分)如图所示,在等腰直角三角形ABC中,AC=4厘米,BC是半圆的直径,A为扇形ACD的圆心,求阴影部分的面积是多少平方厘米。
2020-2021学年四川省成都市温江区六年级(上)期末数学试卷
参考答案与试题解析
一、选择题(本大题共20小题,每小题1.5分,共30分)
1.【分析】令小正方形的边长是1,则整幅图可以看成是长是10,宽是5的长方形,根据长方形的面积=长×宽求出整个图形的面积;梯形的上底是3,下底是6,高是3,根据梯形的面积=(上底+下底)×高÷2求出梯形的面积,再用梯形的面积除以整个图形的面积即可。
【解答】解:令小正方形的边长是1,
10×5=50
(3+6)×3÷2
=9×3÷2
=13.5
13.5÷50=27%
答:梯形部分占整幅图的27%。
故选:C。
【点评】解决本题先分别根据长方形和梯形的面积公式分别求出两者的面积,再根据求一个数是另一个数百分之几的方法求解。
2.【分析】每两人握一次,那么每个人要握9次;10个人一共握9×10次,但这样算每次握手就算成了2次,所以再除以2即可。
【解答】解:10×(10﹣1)÷2
=90÷2
=45(次)
答:一共要握手45次。
故选:A。
【点评】本题属于握手问题,根据握手总次数的计算方法来求解,握手次数总和的计算方法:握手次数=人数×(人数﹣1)÷2,握手次数的公式要记住,并灵活运用。
3.【分析】根据合格率=合格产品数÷产品总数×100%,合格数是a,总数是a+b,由此代入数据解答即可。
【解答】解:根据分析可得:
工厂质检员检查一批零件,合格的为a件,不合格的为b件,这批零件的合格率是×100%。
故选:D。
【点评】本题主要考查了学生对合格率公式的掌握情况,注意要乘上100%。
4.【分析】先算出第一段占全长的几分之几,再与第二段比较大小即可。
【解答】解:1﹣
所以第一段长。
故选:A。
【点评】本题注意两个三分之一的区别,这是一道易错的题目。
5.【分析】本息=本金×年利率×存期+本金,由此代入数据,进而得解。
【解答】解:8000×2.10%×2+8000
=8000×(1+2.10%×2)
=8336(元)
答:到期后爸爸可得本息一共8336元。
故选:C。
【点评】这种类型属于利息问题,运用关系式“本息=本金+本金×年利率×存期”,找清数据,代入公式计算即可。
6.【分析】把差看作单位“1”,由减数是差的,可得减数为,利用被减数=差+减数,可得被减数=,再求出被减数与差的最简整数比即可。
【解答】解:(1+):1
=:1
=5:3。
故选:D。
【点评】关键是找准单位“1”,再根据减数、被减数与差之间的关系解决问题。
7.【分析】把总质量看作是单位“1“,4×表示的是第一次运走了多少吨;根据减法的意义,4×﹣表示的是第一次比第二次多运了多少吨。
【解答】解:4×表示的是第一次比第二次多运了多少吨。
故选:D。
【点评】解决本题注意找清楚每个数据表示的含义,再根据分数乘法的意义找出乘法部分表示的含义,进而解决问题。
8.【分析】甲商场:根据“一件商品先涨价10%”,确定把原价看作单位“1”,由“后再降价10%”,可知把涨价10%后的价格看作单位“1”,求出现价即可;乙商场:某商品先降价10%的价格是原价的(1﹣10%),后又涨价10%是原价的(1﹣10%)的(1+10%),即是原价的(1﹣10%)×(1+10%),然后比较即可。
【解答】解:假设原价为单位“1”
1×(1+10%)×(1﹣10%)
=1×1.1×0.9
=0.99
=99%
(1﹣10%)×(1+10%)
=0.9×1.1
=99%
现价都是原价的99%
答:最后两店的价格相同。
故选:C。
【点评】完成此题,注意单位“1”的确定,通过比较两店商品现价是原价的百分之几,解决问题。
9.【分析】把甲地到乙地的路程看做单位“1”,去时的速度可以看做是每小时行全程的,返回的速度可以看做每小时行全程的,再求一个数是另一个数的几分之几是多少,用除法进行解答即可。
【解答】解:÷×100%
=0.8×100%
=80%
故选:C。
【点评】灵活运用公式速度=路程÷时间,本题关键在于理解去时和返回的路程是一样的。
10.【分析】按照方案一,甲、乙、丙三人分得数量的比是3:4:5,其中乙分得;按照方案二,甲、乙、丙三人分得数量的比是2:3:4,其中乙分得;然后根据分数大小比较的方法进行比较即可。
【解答】解:4÷(3+4+5)
=4÷12
=
3÷(2+3+4)
3÷9
=
答:两种方案乙分得的数量一样多。
故选:A。
【点评】此题考查的目的是理解掌握比的意义及应用,分数大小比较的方法及应用。
11.【分析】根据几何体从上面、正面和左面看到的形状判断,搭成这个鸡和体,下面需要4个小正方体,分两排,上面1个,下面3个,右齐;上面1个放在前排左侧的小正方体上面.据此可知:至少需要4+1=5(个)小正方体.据此解答.
【解答】解:根据分析可知:
一个立体图形,从上面看到的形状是,从正面看到的形状是,从左面看到的形状是.要搭成这个立体图形至少需要5个小正方体.如图:
故选:B。
【点评】本题是考查从不同方向观察物体和几何图形.是培养学生的观察能力.
12.【分析】本题根据图形覆盖现象规律,屋檐E处与广告牌顶点连线的延长线得出,得出三角形ABD为监视器盲区。
【解答】解:根据图形覆盖现象规律,
E处与广告牌BD的顶点连线的延长线到地面A点,
得出三角形ABD区域为监视器盲区。
故选:C。
【点评】此题考查了简单图形覆盖现象中的规律,解答此题的关键是,根据所给出E处与广告牌顶点D连线并延长,得出视频盲区,解决问题。
13.【分析】根据题干叙述,结合淘气离家的距离变化进行分析即可。
【解答】解:淘气的这一过程可分成以下几段:
(1)从家出发到途中交谈前,这一段时间里离家的距离越来越远;
(2)途中交谈,这一段时间离家的距离不变;
(3)途中交谈后到超市,这一段时间里离家的距离越来越远;
(4)在超市买东西,这一段时间离家的距离不变;
(5)从超市回家,这一段时间里离家的距离越来越近。
只有选项D符合这一变化。
故选:D。
【点评】解答本题的关键是看懂图意,再根据图意进行分析、判断。
14.【分析】根据圆的周长公式:C=2πr,那么r=,再根据圆的面积公式:S=πr2,因为圆周率一定,所以圆的半径和周长成正比例,圆的面积和半径的平方成正比例。据此解答。
【解答】解:因为圆周率一定,所以圆的半径和周长成正比例,大圆的周长是小圆周长的2倍,也就是大圆的半径是小圆半径的2倍,那么大圆的面积就是小圆面积的4倍。
2×2=4
答:大圆的面积是小圆面积的4倍。
故选:B。
【点评】此题主要考查圆的周长公式、面积公式的灵活运用,以及比的意义及应用。
15.【分析】阴影部分面积等于正方形面积减去空白区域的面积,分别计算空白区域面积,作出比较即可。
【解答】解:阴影部分面积等于正方形面积减去空白区域的面积,而三个图的正方形边长相等,所以面积相等,
所以,只需要比较空白区域面积即可,
甲空白区域是4个半径为(4÷2)厘米圆的,也就是一个半径为(4÷2)厘米圆的面积;
乙空百区域是两个半径为(4÷2)厘米的半圆,也就是一个半径为(4÷2)厘米圆的面积;
丙空白区域是一个半径为(4÷2)厘米圆的面积;
所以,甲、乙、丙空白区域面积相等,
所以,甲、乙、丙阴影部分面积也相等。
故选:D。
【点评】本题主要考查了圆与组合图形,将阴影部分面积比较转化为空白区域比较,是本题解题的关键。
16.【分析】由图可知,长方形的宽是圆的直径,长是三个圆的半径,根据比的意义求解即可。
【解答】解:长方形的长为三个圆的半径,宽是圆的直径,即两个圆的半径,
长:宽=3个半径:2个半径=3:2。
故选:B。
【点评】本题主要考查了圆与组合图形,题目较为简单,能够直观的发现长方形长宽与圆半径之间的关系,是本题解题的关键。
17.【分析】根据圆的周长公式:C=πd,因为大圆内3个圆的直径和等于大圆的直径,所以这三个圆的周长和就等于大圆的周长,据此解答即可。
【解答】解:3.14×5=15.7(厘米)
答:三个小圆的周长和是15.7厘米。
故选:B。
【点评】此题主要考查圆的周长公式的灵活运用,关键是熟记公式。
18.【分析】根据圆面积公式的推导过程可知,把一个圆转化为一个近似长方形后面积不变。把圆的面积看作单位“1”,通过观察图形可知,阴影部分的面积相当于该圆面积的(1),再根据比的意义解答即可。
【解答】解:(1):1
=:1
=3:4
答:阴影部分的面积与圆面积的最简整数比是3:4。
故选:C。
【点评】此题考查的目的是理解掌握圆面积公式的推导过程及应用,以及比的意义的应用。
19.【分析】根据圆的周长公式:C=2πr,正方形的周长公式:C=4a,那么a=C÷4,把数据代入公式解答。
【解答】解:2×3.14×a÷4
=6.28a÷4
=1.57a(分米)
答:正方形的边长是1.57a分米。
故选:A。
【点评】此题主要考查圆的周长公式、正方形的周长公式的灵活运用,关键是熟记公式。
20.【分析】图乙看到的是房子的侧面,所以只能是②或④位置看到的,而小路在房子的左侧,树在房子后面,只能是从②位置看到的,据此解答。
【解答】解:图乙看到的是房子的侧面,所以只能是②或④位置看到的,
而小路在房子的左侧,树在房子后面,只能是从②位置看到的。
故选:B。
【点评】本题主要考查了从不同方向观察物体,根据看的图形反向推理,是本题解题的关键。
二、计算(本大题共4小题,共23分)
21.【分析】根据分数、小数以及百分数加减乘除法的计算方法直接进行口算即可。
【解答】解:
(1)1﹣27%=0.73
(2)+25%=1
(3)15×30%=4.5
(4)45÷45%=100
(5)﹣=
(6)+=
(7)1÷×=
(8)3÷÷=36
【点评】本题属于基本的计算,在平时注意积累经验,逐步提高运算的速度和准确性。
22.【分析】根据比的基本性质,即比的前项和后项同时乘或除以一个相同的数(0除外)比值不变,进而把比化成最简比;再用比的前项除以后项即得比值。
【解答】解:(1)0.8:
=(0.8×15):(×15)
=12:10
=6:5
0.8:
=0.8÷
=1.2;
(2)0.07:4.2
=(0.07÷0.07):(4.2÷0.07)
=1:60
0.07:4.2
=0.07÷4.2
=;
(3):
=(×20):(×20)
=8:5
:
=÷
=。
【点评】此题考查化简比和求比值的方法,要注意区分:化简比的结果是一个比,它的前项和后项都是整数,并且是互质数;而求比值的结果是一个数,可以是整数、小数或分数。
23.【分析】(1)先算除法再算加法;
(2)按照乘法分配律计算;
(3)先算小括号里面的乘法,再算小括号里面的减法,最后算括号外面的除法;
(4)按照乘法分配律计算。
【解答】解:(1)7÷+÷7
=10+
=10
(2)3×8×(+75%)
=3×8×+3×8×75%)
=8+18
=26
(3)(﹣×)÷
=(﹣)÷
=×
=
(4)0.8×7.7﹣80%+3.3×
=0.8×(7.7﹣1+3.3)
=0.8×10
=8
【点评】本题考查了四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
24.【分析】(1)先化简方程,再根据等式的性质,方程两边同时除以75%求解;
(2)根据等式的性质,方程两边同时减去,再两边同时除以求解。
【解答】解:(1)x﹣25%x=
75%x=
75%x÷75%=÷75%
x=
(2)x+=4
x+=4
x=3
x=3
x=5.5
【点评】此题考查了学生根据等式的性质解方程的能力,注意等号对齐。
三、操作题(本大题共2小题,每小题6分,共12分)
25.【分析】(1)用A等人数除以所在总人数的百分数即可。
(2)用B等的学生人数除以总人数。
(3)根据条形统计图中的数据及调查总人数,计算各类人数占总人数的百分率,完成作图。
(4)用800乘D类成绩所占百分率,计算即可。
【解答】解:(1)8÷20%=40(人)
答:这次调查共抽取了40名学生的科学成绩。
(2)22÷40×100%
=0.55×100%
=55%
答:B等的学生人数占抽样学生人数的55%。
(3)4÷40×100%
=0.1×10%
=10%
1﹣55%﹣20%﹣10%=15%
40﹣8﹣22﹣4=6(名)
统计图如下:
(4)800×15%=120(名)
答:这次模拟考试大约有120名学生的科学成绩为D等。
故答案为:40;55%;120。
【点评】本题主要考查统计图表的填充,关键根据统计表中的数据完成统计图并回答问题。
26.【分析】根据图示,阴影部分的周长等腰半径是4厘米的圆的面积是四分之一加上5厘米和6厘米的两条线段的长;面积等于梯形面积减去圆的面积的四分之一。
【解答】解:3.14×4×2÷4+5+6
=6.28+11
=17.28(厘米)
(4+6)×4÷2﹣3.14×42÷4
=20﹣12.56
=7.44(平方厘米)
答:阴影部分的周长是17.28厘米,面积是7.44平方厘米。
【点评】本题主要考查组合图形的周长和面积,关键是把不规则图形转化为规则图形,再计算。
四、解决问题(本大题共5小题,每小题5分,共25分)
27.【分析】先把城市的总数量看成单位“1”,其中约有的城市供水不足,用城市的总数量乘,求出供水不足的城市有多少个;再把供水不足的城市数看成单位“1”,再乘就是严重缺水的城市有多少个。
【解答】解:60××
=40×
=10(个)
答:全国严重缺水的城市大约有10个。
【点评】解答此题的关键是分清两个不同的单位“1”,已知单位“1”的量,求它的几分之几是多少用乘法求解。
28.【分析】把八月份的用水量看成单位“1”,并设八月份的用水量是x吨;九月份比八月份节约了,那么九月份的用水量是八月份的(1﹣),根据八月份的用水量×(1﹣)=九月份的用水量列出方程求解。
【解答】解:设八月份的用水量是x吨。
(1﹣)x=14
x=14
x=18
答:淘气家八月份用水18吨。
【点评】解决本题关键是找出单位“1”,根据分数乘法的意义找出等量关系,再列出方程求解。
29.【分析】根据圆的周长公式:C=2πr,把数据代入公式求出车轮的周长,用车轮的周长乘每分钟转的圈数求出每分钟行驶的速度,然后根据路程=速度×时间,据此列式解答。
【解答】解:1小时=60分
2×3.14×0.4×500×60
=2.512×500×60
=1256×60
=75360(米)
75360米=75.36千米
答:这辆汽车1小时可以行驶75.36千米。
【点评】此题主要考查圆的周长公式的灵活运用,关键是熟记公式。
30.【分析】首先根据环形面积公式;S=π(R2﹣r2),求出花坛的面积,花坛的面积按3:5的比例种植草和花,去种花的面积占花坛面积的,根据一个数乘分数的意义,用乘法解答。
【解答】解:3+5=8
20÷2=10(米)
3.14×(102﹣22)×
=3.14×(100﹣4)×
=3.14×96×
=301.44×
=188.4(平方米)
答:种花的面积是188.4平方米。
【点评】此题主要考查环形面积公式的灵活运用,关键是熟记公式。
31.【分析】根据甲工程队完成4000米时,甲正好完成工程总长的,把工程总长看作单位”1“,根据分数除法的意义,用4000米除以求出工程总长,根据甲工程队完成总工程的30%,余下的任务由乙、丙两个工程队完成,则乙、丙两个工程队一共完成总长的(1﹣30%),根据百分数乘法的意义,用工程总长乘(1﹣30%)求出乙、丙两个工程队一共完成的长度,再根据余下的任务由乙、丙两个工程队按3:4进行分配,则丙工程队完成乙、丙两个工程队的总长度的,所以再用乙、丙两个工程队一共完成的长度乘即可解答。
【解答】解:4000÷×(1﹣30%)×
=18000×
=18000×
=7200(米)
答:丙工程队应完成的工程量是7200米。
【点评】本题考查了学生根据分数乘法和分数除法的意义解答应用题的能力。
五、附加题.填空题。(本大题共5小题,共10分)
32.【分析】九折是指售价是定价的90%,先把定价看成单位“1”,用100元乘90%求出售价;此时仍能获20%的利润,是指售价比进价多20%,是把进价看成单位“1”,它的(1+20%)就是售价,再用售价除以这个百分数即可求出进价。
【解答】解:100×90%=90(元)
90÷(1+20%)
=90÷120%
=75(元)
答:这件商品的进价是75元。
故答案为:75。
【点评】解答此题的关键是分清两个单位“1”的区别,求单位“1”的百分之几用乘法求解;已知单位“1”的百分之几是多少,求单位“1”用除法求解。
33.【分析】根据圆的周长公式:C=2πr,再根据直径半径的关系,d=2r,设圆的半径为r厘米,已知一个圆的周长、直径、半径相加的和是27.84厘米,据此求出 半径,然后根据圆的面积公式;S=πr2,把数据代入公式解答。
【解答】解:设圆的半径为r厘米
2×3.14×r+2r+r=27.84
6.28r+2r+r=27.84
9.28r=27.84
r=3
3.14×32
=3.14×9
=28.26(平方厘米)
答:这个圆的面积是28.26平方厘米。
故答案为:28.26。
【点评】此题考查的目的是理解掌握直径与半径的关系,圆的周长公式、面积公式的灵活运用,关键是熟记公式。
34.【分析】如图:由题意知:两个正方形中阴影部分面积比是3:1,又因这两个三角形等底,所以这两个三角形高的比是3:1,即BC=3CG,从而可算出这两个正方形的面积,则空白部分的面积等于每个正方形的面积去掉每个阴影部分的面积,从而算出它们的面积比.
【解答】解:因为S△BCE=×CE×BC,
又因为CE=CG,
S△GCE=CE×CG=×CG2,
又因为S△BCE:S△GCE=3:1,
所以 ×CE×BC:×CE×CG=3:1,
即BC:CG=3:1,
BC=3CG,
所以S正方形ABCD=BC2=3CG×3CG=9CG2,
S正方形ECGF=CG2,
又因为S△BCE=×CE×BC,CE=CG,
即S△BCE=×CE×3CG=×CG2,
所以大正方形中j甲图的面积是:
S正方形ABCD﹣S△BCE=9CG2﹣CG2=CG2,
小正方形乙图的面积是:S正方形EFGCDE面积=CG2
所以两空白部分的面积比是:CG2:CG2=15:1.
答:空白部分甲和乙的面积比是15:1.
故答案为:15:1.
【点评】此题解决的突破口在于先根据图形特点及两个阴影部分的比,找准两个正方形边的关系,用含字母的式子来代换,从而解决问题.
35.【分析】假设小圆的半径为r,大圆的半径为R,则小正方形的边长为r,大正方形边长为R,阴影部分面积=R2﹣r2=8(平方厘米),根据圆环的面积公式:S=π(R2﹣r2)整体代入求解即可。
【解答】解:设小圆的半径为r厘米,大圆的半径为R厘米,
则小正方形的边长为r厘米,大正方形边长为R厘米,
阴影部分面积=R2﹣r2=8(平方厘米),
圆环的面积:
3.14×(R2﹣r2)
=3.14×8
=25.12(平方厘米)
答:圆环的面积是25.12平方厘米。
故答案为:25.12。
【点评】本题主要考查了圆与组合图形,假设未知数然后进行整体代换是本题解题的关键。
36.【分析】如图所示:蓝色部分的面积加上阴影部分的面积就是纸片折叠后所覆盖桌面的面积,由题意知所覆盖桌面的面积占原长方形面积的,而原长方形的面积等于蓝色部分的面积的2倍与阴影部分的面积之和,据此,可设蓝色部分的面积为x平方厘米,则纸片折叠后所覆盖桌面的面积是(x+2)平方厘米,原长方形的面积是(2x+2)平方厘米,由所覆盖桌面的面积占原长方形面积的,可列方程x+2=(2x+2),再依据等式的性质解方程即可解决。
【解答】解:如上图所示:设蓝色部分的面积为x平方厘米,则原长方形的面积是(2x+2)平方厘米,根据题意得:
x+2=(2x+2)
x+2=x+
x=
x=4
所以原长方形的面积是:
2x+2
=2×4+2
=8+2
=10
答:原长方形的面积是10平方厘米。
故答案为:10。
【点评】本题数量之间的关系较为复杂,用方程解决比较好理解.关键是明确数量关系:原长方形的面积等于蓝色部分的面积的2倍与阴影部分的面积之和。
六、解答题本大题共2小题,每小题5分,共10分)
37.【分析】在加工剩下的1﹣=零件时,工效变为原来的(1+20%)=,那么所用时间就是原来加工这部分零件所用时间的,比原来少用.所以,提前的10天时间,就是原时间的:10÷=60天;则原计划加工这批零件的时间为60=150天,从而可求出这批零件的总量.
【解答】解:在加工剩下的1﹣=零件时,工效变为原来的(1+20%)=,
那么所用时间就是原来加工这部分零件所用时间的,比原来少用.
所以,提前的10天时间,就是原时间的:10÷=60(天);
则原计划加工这批零件的时间为60=150(天);
这批零件共有:15×150=2250(个).
答:这批零件共有2250个.
【点评】此题主要考查工作量、工作时间、工作效率之间的关系,关键是先求出提高工效后的时间,从而逐步得解.
38.【分析】将图形分割,将阴影部分面积转化为两部分,一部分是扇形ACD面积与三角形ABC面积一半的差,另一部分是半圆形BEC的面积与三角形ABC面积一半的差,相加即可。
【解答】解:如图分割:
阴影部分①的面积=扇形ACD面积﹣三角形ACE的面积,
阴影部分②的面积=半圆BEC面积﹣三角形BCE的面积,
三角形ACE的面积+三角形BCE的面积=三角形ABC的面积,
阴影部分面积=扇形ACD的面积+半圆BEC的面积﹣三角形ABC的面积
=×3.14×42+×3.14×(4÷2)2﹣×4×4
=×3.14×16+×3.14×4﹣8
=6.28+6.28﹣8
=12.56﹣8
=4.56(平方厘米)
答:阴影部分的面积是4.56平方厘米。
【点评】本题主要考查了圆与组合图形的面积,将要求的面积合理分割,转化为规则图形的面积差是本题解题的关键。
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2021/4/27 16:01:25;用户:18538596816;邮箱:18538596816;学号:27024833
四川省成都市温江区2023-2024学年五年级下学期期末数学试卷: 这是一份四川省成都市温江区2023-2024学年五年级下学期期末数学试卷,共6页。
2020-2021年四川成都市温江区六年级上册期末数学试卷及答案(北师大版): 这是一份2020-2021年四川成都市温江区六年级上册期末数学试卷及答案(北师大版),共26页。试卷主要包含了选择题,计算,操作题,解决问题,附加题等内容,欢迎下载使用。
四川省成都市温江区实验外国语学校附属小学2023-2024学年六年级上学期期末数学试卷: 这是一份四川省成都市温江区实验外国语学校附属小学2023-2024学年六年级上学期期末数学试卷,共5页。试卷主要包含了填空,选择,计算,动手操作,解决问题等内容,欢迎下载使用。













