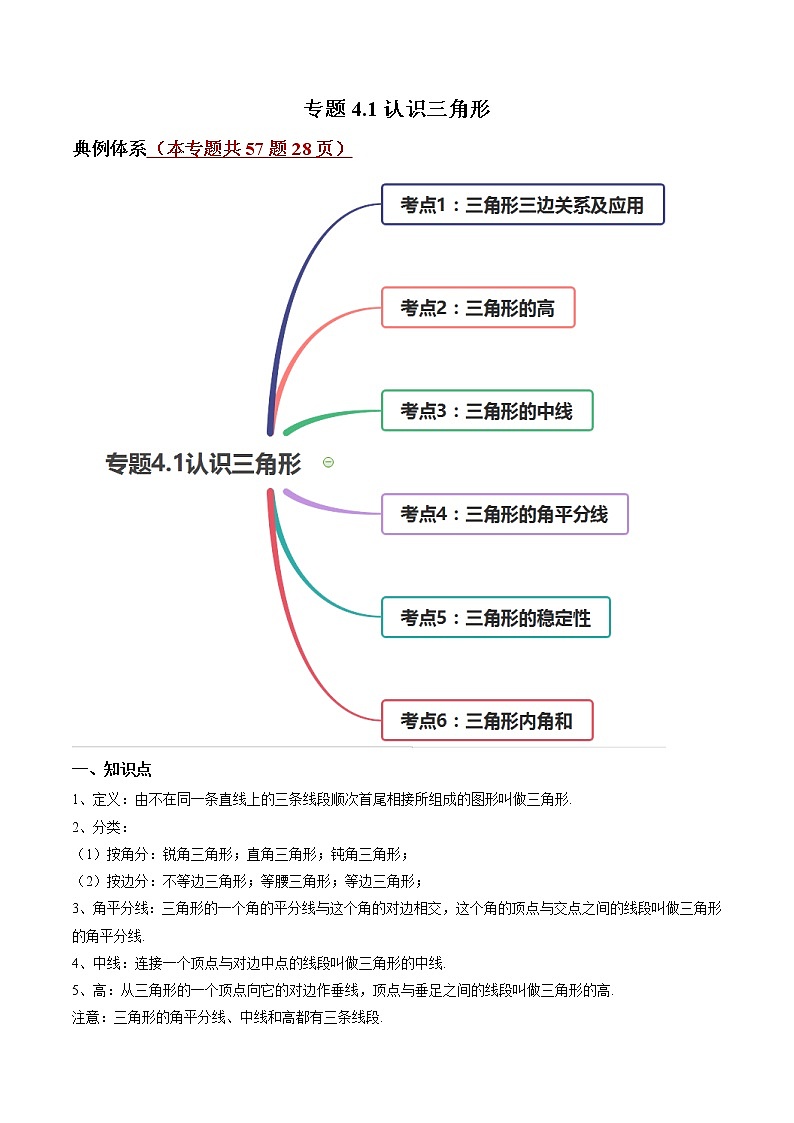
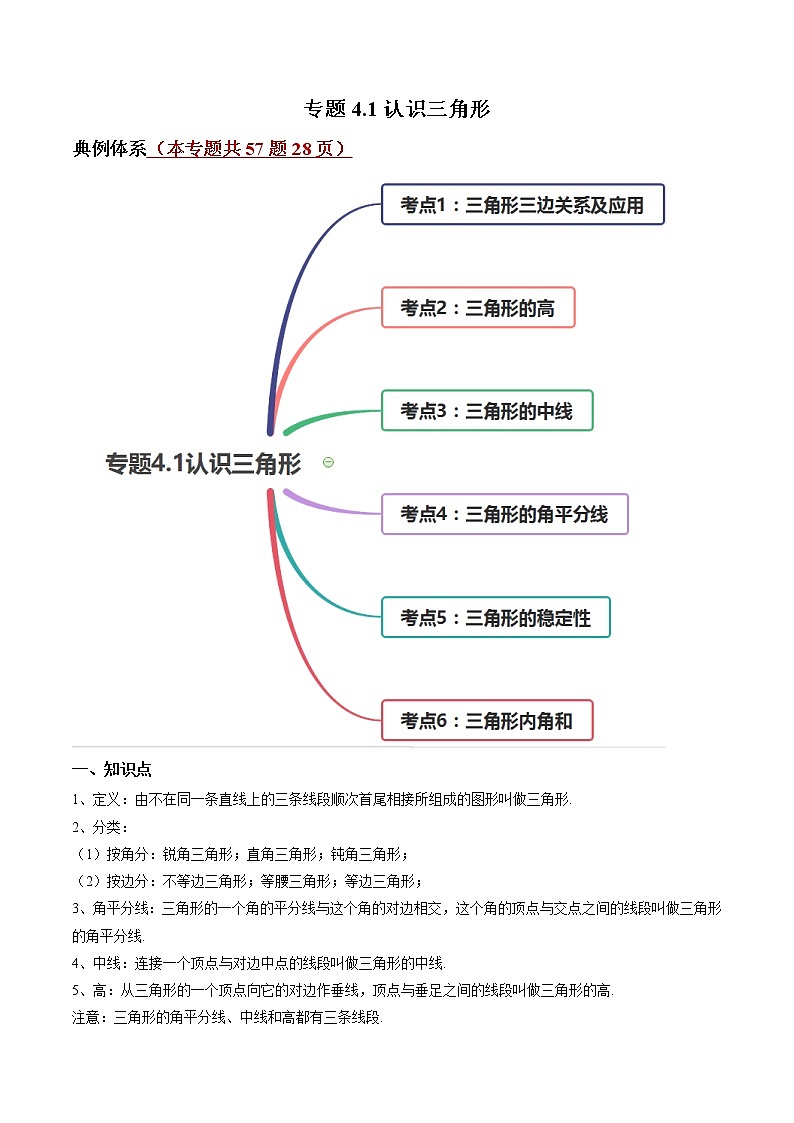
专题4.1认识三角形（讲练）-简单数学之2021-2022学年七年级下册同步讲练（北师大版）

这是一份专题4.1认识三角形（讲练）-简单数学之2021-2022学年七年级下册同步讲练（北师大版），文件包含专题41认识三角形讲练-简单数学之2021-2022学年七年级下册同步讲练解析版北师大版docx、专题41认识三角形讲练-简单数学之2021-2022学年七年级下册同步讲练原卷版北师大版docx等2份试卷配套教学资源，其中试卷共41页， 欢迎下载使用。

专题4.1认识三角形
典例体系（本专题共57题28页）

一、知识点
1、定义：由不在同一条直线上的三条线段顺次首尾相接所组成的图形叫做三角形.
2、分类：
（1）按角分：锐角三角形；直角三角形；钝角三角形；
（2）按边分：不等边三角形；等腰三角形；等边三角形；
3、角平分线：三角形的一个角的平分线与这个角的对边相交，这个角的顶点与交点之间的线段叫做三角形的角平分线.
4、中线：连接一个顶点与对边中点的线段叫做三角形的中线.
5、高：从三角形的一个顶点向它的对边作垂线，顶点与垂足之间的线段叫做三角形的高.
注意：三角形的角平分线、中线和高都有三条线段.
6、三角形的稳定性.
7、三角形的内角：三角形的内角和等于。

如图：
二、考点点拨与训练
考点1：三角形三边关系及应用
典例：（2020·浙江省中考真题）长度分别为2，3，3，4的四根细木棒首尾相连，围成一个三角形（木棒允许连接，但不允许折断），得到的三角形的最长边长为（　　）
A．4 B．5 C．6 D．7
【答案】B
【解析】
①长度分别为5、3、4，能构成三角形，且最长边为5；
②长度分别为2、6、4，不能构成三角形；
③长度分别为2、7、3，不能构成三角形；
④长度分别为6、3、3，不能构成三角形；
综上所述，得到三角形的最长边长为5．
故选：B.
方法或规律点拨
此题考查构成三角形的条件，三角形的三边关系，解题中运用不同情形进行讨论的方法，注意避免遗漏构成的情况.
巩固练习
1．（2019·河北省初一期末）小芳有两根长度为和的木条，她想钉一个三角形木框，桌上有下列长度的几根木条，她应该选择长度为（ ）的木条.
A． B． C． D．
【答案】C
【解析】
设木条的长度为，则，即，
故她应该选择长度为的木条.
故选
2．（2020·偃师市实验中学初一月考）已知a>b>c>0，则以a、b、c为三边组成三角形的条件是（ ）
A．b+c>a B．a+c>b C．a+b>c D．以上都不对
【答案】A
【解析】解：已知a＞b＞c＞0，则以a，b，c为三边组成三角形的条件是b+c＞a．
故选：A．
3．（2019·河南省初一期末）若三角形两边的长分别为7cm和2cm，第三边的长为奇数，则第三边的长为（ ）
A．3 B．5 C．7 D．9
【答案】C
【解析】解：设第三边的长为x，
∵7+2=9，7﹣2=5，
∴5 ∵x为奇数，
∴x=7.
故选C
4．（2020·河北省初一月考）下列长度的各边能组成三角形的是（ ）
A．3cm、12cm、8cm B．6cm、8cm、15cm
C．2cm、3cm、5cm D．6.3cm、6.3cm、12cm
【答案】D
【解析】
三角形的三边关系定理：任意两边之和大于第三边，任意两边之差小于第三边
A、，不满足三角形的三边关系定理，则不能组成三角形
B、，不满足三角形的三边关系定理，则不能组成三角形
C、，不满足三角形的三边关系定理，则不能组成三角形
D、，满足三角形的三边关系定理，则能组成三角形
故选：D．
5．（2020·四川省初一期中）下列线段中能围成三角形的是（　　）
A．1，2，3 B．4，5，6 C．5，6，11 D．7，10，18
【答案】B
【解析】
解：A、1+2＝3，所以不能围成三角形；
B、4+5＞6，所以能围成三角形；
C、6+5＝11，所以不能围成三角形；
D、7+10＜18，所以不能围成三角形；
故选：B．
6．（2020·河北省初一月考）已知三角形的边长都是整数，其中两边分别为5和1，则三角形的周长为________。
【答案】11
【解析】
解：∵三角形的两边的长为5和1，
∴第三边的取值范围是4≤x<6，
∵三角形的三边长都是整数，
∴第三边的长为5，
∴周长为：5+5+1=11，
故答案为11．
7．（2020·四川省初一期中）已知，，是的三边长，，满足，为奇数，则________．
【答案】7
【解析】
∵，
∴a-7=0，b-1=0，
∴a=7，b=1
由三角形三边关系可知，7-1＜c＜7+1，即6＜c＜8，
∵为奇数，
∴c=7，
故答案为：7.
8．（2020·黑龙江省初二期末）已知非等腰三角形的两边长分别是2 cm和9 cm,如果第三边的长为整数,那么第三边的长为（ ）
A．8 cm或10 cm B．8 cm或9 cm C．8 cm D．10 cm
【答案】A
【解析】
解：根据三角形的三边关系，得
7cm＜第三边＜11cm，
故第三边为8，9，10，
又∵三角形为非等腰三角形，
∴第三边≠9．
故选：A．
9．（2020·扬州市江都区第三中学初三二模）小明想做一个三角形的框架，他有两根长度分别为和的细木条，需要将其中一根木条分为两段，如果不考虑损耗和接头部分，那么他可以把（　　）分为两截．
A．的木条 B．的木条 C．两根都可以 D．两根都不行
【答案】B
【解析】
解：当10cm 为第三边时，另外两边之和为11cm，大于第三边，故可以把11cm的木条分为两截；
当11cm为第三边时，另外两边之和为10cm，不满足两边之和大于第三边，故不能做成三角形支架．
故选B．
10．（2019·山西省初一月考）现有两条线段长度分别为和另有条线段，长度分别为这条线段中，可以与线段组成三角形的线段长度是（ ）
A． B． C． D．
【答案】C
【解析】
设第三边为
∵
∴即
故选：C．
考点2：三角形的高
典例：（2020·北京初三二模）如图，用三角板作的边上的高线，下列三角板的摆放位置正确的是（ ）
A． B．C． D．
【答案】B
【解析】
解：A．作出的是△ABC中BC边上的高线，故本选项错误；
B．作出的是△ABC中AB边上的高线，故本选项正确；
C．不能作出△ABC中AB边上的高线，故本选项错误；
D．作出的是△ABC中AC边上的高线，故本选项错误；
故选：B．
方法或规律点拨
本题考查的是作图-基本作图，熟知三角形高线的定义是解答此题的关键．
巩固练习
1．（2020·北京初三二模）如图，在中，，通过测量，并计算的面积，所得面积与下列数值最接近的是（ ）

A． B． C． D．
【答案】D
【解析】
如图，过点C作CD⊥AB，垂足为点D，则CD为AB边上的高，

经过测量，CD≈2cm
所以，
故选：D.
2．（2020·江苏省初一期中）在下列各图的△ABC中，正确画出AC边上的高的图形是(　　)
A． B．
C． D．
【答案】C
【解析】
解：AC边上的高就是过B作垂线垂直AC交AC的延长线于D点，因此只有C符合条件，
故选：C．
3．（2020·常州市第二十四中学初一期中）在下列图形中，正确画出△ABC的AC边上的高的图形是（　　）
A． B．
C． D．
【答案】C
【解析】
解：△ABC的AC边上的高的就是通过顶点B作的AC所在直线的垂线段．根据定义正确的只有C．
故选：C．
4．（2020·湖北省武汉市江汉区教育局初二月考）下列四个图形中，线段BE是△ABC的高的是（ ）
A．B．C．D．
【答案】D
【解析】根据三角形的高线的定义可得，则D选项中线段BE是△ABC的高.
5．（2019·湖北省初二期中）如图，过△ABC的顶点A，作BC边上的高，以下作法正确的是（ ）
A．B．C． D．
【答案】A
【解析】
根据定义可得A是作BC边上的高，C是作AB边上的高，D是作AC边上的高.
故选A.
6．（2020·邵东县创新实验学校初二期中）在数学课上，同学们在练习画边上的高时，出现下列四种图形，其中正确的是（ ）
A． B．
C． D．
【答案】C
【解析】
根据高的定义，AC边上的高应该是从点B出发向AC边作垂线
A中，AE不是高，故该选项错误；
B中，所作的CE为AB边上的高，不符合题意，故该选项错误；
C中，BE为AC边上的高，故该选项正确；
D中，AE不是高，故该选项错误；
故选：C．
7．（2020·余干县第二中学初一月考）在数学课上，同学们在练习过点B作线段AC所在直线的垂线段时，有一部分同学画出下列四种图形，请你数一数，错误的个数为( )

A．1个 B．2个 C．3个 D．4个
【答案】D
【解析】从左向右第一个图形中，BE不是线段，故错误；
第二个图形中，BE不垂直AC，所以错误；
第三个图形中，是过点E作的AC的垂线，所以错误；
第四个图形中，过点C作的BE的垂线，也错误.
故选D.
8．（2019·苏州市景范中学校初一期中）如果一个三角形的三条高的交点恰好是这个三角形的一个顶点，那么这个三角形是（ ）
A．锐角三角形 B．直角三角形 C．钝角三角形 D．不能确定
【答案】B
【解析】因为直角三角形的三条高线的交点是直角顶点，而其他三角形三条高线的交点都不在顶点上，所以如果一个三角形的三条高的交点恰好是这个三角形的一个顶点，那么这个三角形是直角三角形．
故选B．
9．（2020·河南省初一月考）如图，在Rt△ABF中，∠F=90°，点C是线段BF上异于点B和点F的一点，连接AC，过点C作CD⊥AC交AB于点D，过点C作CE⊥AB交AB于点E，则下列说法中，错误的是（ ）

A．△ABC中，AB边上的高是CE B．△ABC中，BC边上的高是AF
C．△ACD中，AC边上的高是CE D．△ACD中，CD边上的高是AC
【答案】C
【解析】
解：根据三角形某边上的高的定义验证：
A. △ABC中，AB边上的高是CE，故A正确；
B. △ABC中，BC边上的高是AF，故B正确；
C. △ACD中，AC边上的高是CD，故C错误；
D. △ACD中，CD边上的高是AC，故D正确；
故选C．
10．（2020·江苏省初一月考）如图，每个小正方形的边长为1，在方格纸内将△ABC经过一次平移后得到△A'B'C'，图中标出了点B的对应点B'．利用网格点和三角板画图：
（1）补全△A'B'C'根据下列条件；
（2）画出△ABC中AB边上的中线CD；
（3）画出△ABC中BC边上的高线AE；
（4）线段A'B'与AB的关系是　　　　．△A'B'C'的面积为　　　　．

【答案】（1）作图见详解（2）作图见详解（3）作图见详解（4）平行且相等；8．
【解析】
（1）、（2）、（3）如下图所示：

（3）根据图形平移的性质可知，AB∥A'B'，且AB=A'B′；
∴ S△A'B'C' = ，
故应填：平行且相等；8.
考点3：三角形的中线
典例：（2019·河北省初一期末）如图，D，E，F分别是边BC，AD，AC上的中点，若S阴影的面积为3，则△ABC的面积是（　　）

A．5 B．6 C．7 D．8
【答案】D
【解析】
∵D为BC的中点
∴，
∴
∴+=+=
∴==×3=8
故选：D
方法或规律点拨
三角形的中线将三角形分成两个面积相等的三角形，根据中线找出图中三角形的面积关系是解决本题的关键.
巩固练习
1．（2020·江苏省苏州草桥中学初一期中）如图，在中，分别是边的中点，且阴影部分面积为，则等于( )

A．6 B．8 C．10 D．12
【答案】D
【解析】
解：∵D是BC的中点，
∴，
∵E是AD的中点， ，
∴，
∵F是CE的中点，


故选：D．
2．（2020·常州市第二十四中学初一期中）如图，在△ABC中，已知点D、E、F分别是BC、AD、BE上的中点，且△ABC的面积为8cm2，则△CEF的面积为（ ）

A．0.5cm2 B．1cm2 C．2cm2 D．4cm2
【答案】C
【解析】解：如图，

∵点D为BC的中点，
∴S△ADC=S△ABC，S△EDC=S△EBC，
∵点E为AD的中点，
∴S△EDC=S△ADC，
∴S△EDC=S△ABC，
∴S△EBC=2S△EDC=S△ABC，
∵F点为BE的中点，
∴S△CEF=S△EBC=×S△ABC=××8=2（cm2）．
故选：C．
3．（2020·长春市第四十七中学初一期中）如图，△ABC 中，点 D 是 AC 边上的中点，点 E 是 AB 边上的中点，若 SDABC =12 ，则图中阴影部分的面积是（ ）

A．6 B．4 C．3 D．2
【答案】C
【解析】
∵点D是AC边上的中点，且SDABC=12；
∴S△ABD=，
又点E是AB边上的中点
∴S△DEB=
即图中阴影部分的面积是3，
故选：C
4．（2020·盐城市盐都区实验初中初一月考）如图，是的中线，、是的三等分点．若的面积为，则的面积为______．

【答案】6
【解析】
∵是的中线
∴
∵，是的三等分点
∴
∴
∴，
故答案为：6.
5．（2020·盐城市初级中学初一期中）如图,已知AE是△ABC的边BC上的中线,若AB=8cm,△ACE的周长比△AEB的周长多2cm,则AC=_____.

【答案】10cm
【解析】
解：∵AE是△ABC的边BC上的中线，
∴CE＝BE，
又∵AE＝AE，△ACE的周长比△AEB的周长多2cm，
∴AC−AB＝2cm，即AC−8cm＝2cm，
∴AC＝10cm，
故答案为10cm.
6．（2020·福建省初一期末）如图，AD是△ABC的中线，G是AD上的一点，且AG=2GD， 连结BG，若，则为_______．

【答案】4
【解析】
∵，
∴S△ABD＝6，
∵AG＝2GD，
∴AG=AD
∴S△ABG＝S△ABD =4，
故答案为：4．
7．（2020·山东省青岛第二十六中学初一期中）如图，△ABC中，点E是BC上的一点，EC＝3BE，点D是AC中点，若S△ABC＝36，则S△ADF－S△BEF ＝_．

【答案】9.
【解析】
∵在△ABC中，E是BC上的一点，EC=3BE，
∴S△ACE=3S△AEB=S△ACB=×36=27，
∵点D是AC的中点，
∴S△ABD=S△CBD=S△ACB=18，
∵设△ABC、△ADF、△BEF的面积分别S、S1、S2，且S=36，
∴S1-S2=27-18=9．
故答案为：9．
8．（2020·江苏省初一期中）如图，在△ABC中，点D为BC边上一点，E、F分别为AD、CE的中点，且=8cm2，则=____．

【答案】2
【解析】
∵点F是CE的中点，
∴△BEF的底是EF，△BEC的底是EC，即EF=EC，高相等；
∴S△BEF=S△BEC，
同理得S△EBC=S△ABC，
∴S△BEF=S△ABC，且S△ABC=8，
∴S△BEF=2，
故答案为：2．
9．（2020·广东省龙岭初级中学初一期中）如图△ABC中，分别延长边AB、BC、CA，使得BD=AB，CE=2BC，AF=3CA，若△ABC的面积为1，则△DEF的面积为________.

【答案】18
【解析】
连接AE和CD，
∵BD=AB，
∴S△ABC=S△BCD=1，S△ACD=1+1=2，
∵AF=3AC，
∴FC=4AC，
∴S△FCD=4S△ACD=4×2=8，
同理可以求得：S△ACE=2S△ABC=2，则S△FCE=4S△ACE=4×2=8；
S△DCE=2S△BCD=2×1=2；
∴S△DEF=S△FCD+S△FCE+S△DCE=8+8+2=18．

考点4：三角形的角平分线
典例：（2018·南京外国语学校初一期中）小明在学习三角形知识时，发现如下三个有趣的结论：在中，，平分，为直线上一点，，为垂足，的平分线交直线于点，回答下列问题并说明．（可在图上标注数字角）
（1）如图①，为边上一点，则、的位置关系是________．请给予证明；

（2）如图②，为边反向延长线上一点，则、的位置关系是________．（请直接写出结论）

（3）如图③，为边延长线上一点，则、的位置关系是________．请给予证明．

【答案】（1），见解析；（2）；（3），见解析
【解析】
解：（1）
证明：∵，
∴；
∵在四边形中，，
∴；
∵平分，
∴；
同理，
∴；
∵，
∴，
∴，
∴．
（2）
（3）
证明：延长交于点，
在与中

∵与为对顶角，
∴；
∵，
∴；
∵，分别平分，，
∴，，
∴；
在与中
，
∵与为对顶角，
∴，
∴，
∴．
方法或规律点拨
本题主要考查了平行线的判定以及角平分线应用和垂线段的判定，是基础知识，需要熟练掌握．
巩固练习
1．（2020·四川省北大附中成都为明学校初一期中）如图，AE是△ABC的角平分线，AD是△AEC的角平分线，若∠BAC＝80°，则∠EAD＝（　　）

A．30° B．45° C．20° D．60°
【答案】C
【解析】
∵∠BAC＝80°，
AE是△ABC的角平分线，
∴∠EAC＝∠BAC＝40°，
∵AD是△AEC的角平分线，
∴∠EAD＝∠EAC＝20°．
故选：C．
2．（2019·四川省广安中学初一期末）如图，点M在线段BC上，点E和N在线段AC上，EM∥AB，BE和MN分别平分∠ABC和∠EMC．下列结论：①∠MBN＝∠MNB；②∠MBE＝∠MEB；③MN∥BE.其中正确的是( )

A．①②③ B．②③ C．①③ D．①②
【答案】B
【解析】
解：∵EM∥AB，
∴∠MEB=∠ABE，∠ABC=∠EMC，
∵BE和MN分别平分∠ABC和∠EMC，
∴∠ABE=∠MBE，∠EMN=∠NMC，
∴∠MEB=∠MBE（故②正确），∠EBM=∠NMC，
∴MN∥BE（故③正确），
∵∠MNB=∠EBN，而∠EBN和∠MBN的关系不知，
∴∠MBN和∠MNB的关系无法确定，故①错误，
综上所述，正确的是：②③
故选：B．
3．（2020·巨野县高级中学初一月考）下列叙述中错误的一项是（     ）．
A．三角形的中线、角平分线、高都是线段．
B．三角形的三条高线中至少存在一条在三角形内部．
C．只有一条高在三角形内部的三角形一定是钝角三角形．
D．三角形的三条角平分线都在三角形内部．
【答案】C
【解析】
A：三角形的中线、角平分线、高都是线段，正确；
B：锐角三角形三条高在三角形内部，直角三角形一条高在三角形内部，钝角三角形一条高在三角形内部，正确；
C：只有一条高在三角形内部的三角形是钝角三角形或直角三角形，错误；
D：锐角三角形、钝角三角形、直角三角形的三条角平分线都在三角形内部，正确
故选：C
4．（2020·巨野县高级中学初一月考）如图，在三角形ABC中，∠1＝∠2，G为AD的中点，延长BG交AC于E．F为AB上的一点，CF⊥AD于H．下列判断正确的有（       ）．

（1）AD是三角形ABE的角平分线．（2）BE是三角形ABD边AD上的中线．（3）CH为三角形ACD边AD上的高．
A．1个 B．2个 C．3个 D．0个
【答案】A
【解析】
根据三角形角平分线的概念，AG为三角形ABE的角平分线，（1）错误；
根据三角形中线的概念，BG是三角形ABD边AD的中线，（2）错误；
根据三角形高的概念，CH为三角形ACD边AD上的高，（3）正确．
故答案选：A．
5．（2020·江苏省初一期中）如图，在△ABC中，AD是高，AE是角平分线，AF是中线，则下列说法中错误的是（ ）

A．BF＝CF B．∠C＋∠CAD＝90° C．∠BAF＝∠CAF D．
【答案】C
【解析】
解：∵AF是△ABC的中线，
∴BF=CF，A说法正确，不符合题意；
∵AD是高，
∴∠ADC=90°，
∴∠C+∠CAD=90°，B说法正确，不符合题意；
∵AE是角平分线，
∴∠BAE=∠CAE，C说法错误，符合题意；
∵BF=CF，
∴S△ABC=2S△ABF，D说法正确，不符合题意；
故选：C．
6．（2020·江西省初一月考）如图，已知△ABC中，AD是BC边上的中线，有以下结论：①AD平分∠BAC；②△ABD的周长－△ACD的周长=AB－AC；③BC=2AD；④△ABD的面积是△ABC面积的一半．其中正确的是（ ）

A．①②④ B．②③④ C．②④ D．③④
【答案】C
【解析】
解：∵△ABC中，AD是BC边上的中线，
∴BD=CD，但AD不一定平分∠BAC，故①错误；
∵△ABD的周长=AB＋BD＋AD，△ACD的周长=AC＋CD＋AD
∴△ABD的周长－△ACD的周长=（AB＋BD＋AD）－（AC＋CD＋AD）
= AB－AC，故②正确；
∵AD是BC边上的中线，
∴BC=2BD，但BD不一定等于AD，
∴BC不一定等于2AD，故③错误；
设点A到BC的距离为h，
∴S△ABD=BD·h，S△ABC=BC·h=×2BD·h= BD·h
∴△ABD的面积是△ABC面积的一半，故④正确．
故正确的结论有②④．
故选C．
7．（2020·偃师市实验中学初一月考）已知：钝角△ABC，请画出△ABC的角平分线BD，AB边上的中线和AC边上的高，并用字母表示．

【答案】角平分线BD、AB边上的中线CE、 AC边上的高BF,画图见解析．
【解析】
解：如图：角平分线BD，AB边上的中线CE和AC边上的高BF即为所求.

8．（2020·江西省初一月考）如图，在△ABC中，AD，AE，AF分别为△ABC的高线、角平分线和中线．

（1）写出图中所有相等的角和相等的线段；
（2）当BF=8cm，AD=7 cm时，求△ABC的面积．
【答案】（1）∠BAE=∠CAE，∠ADC=∠ADB，BF=FC；（2）56cm
【解析】
【分析】
（1）分别根据角平分线定义、三角形的高线和三角形的中线定义解决问题即可；
（2）根据三角形的面积公式列式求解即可．
【详解】
解：（1）∵AE是△ABC的角平分线，
∴∠BAE=∠CAE．
∵AD是△ABC的高，
∴∠ADB=∠ADC=90°．
∵AF是△ABC的中线，
∴BF=CF．
图中所有相等的角和相等的线段为：∠BAE=∠CAE，∠ADB=∠ADC=90°，BF=CF．
（2）∵BF=CF，BF=8cm，AD=7cm，
∴BC=2BF=2×8=16cm，
∴S△ABC=BC•AD=×16cm×7cm
=56cm2．
答：△ABC的面积是56cm2．
考点5：三角形的稳定性
典例：（2020·四川省东坡区百坡中学初一月考）如图所示，一扇窗户打开后，用窗钩AB即可固定，这里所用的几何原理是（ ）

A．两点之间线段最短 B．垂线段最短．
C．两定确定一条直线 D．三角形具有稳定性
【答案】D
【解析】
∵户打开后，用窗钩AB钩住，可以构成一个三角形，
∴所用的几何原理是三角形具有稳定性，
故选：D．
方法或规律点拨
本题考查了三角形的稳定性在实际生活中的应用问题．
巩固练习
1．（2020·湖北省武汉市江汉区教育局初二月考）下列图形具有稳定性的是（　　）
A． B． C． D．
【答案】A
【解析】
A、具有稳定性，符合题意；
B、不具有稳定性，故不符合题意；
C、不具有稳定性，故不符合题意；
D、不具有稳定性，故不符合题意，
故选A．
2．（2020·河北省初三一模）下列图形不具有稳定性的是（　　）
A． B．
C． D．
【答案】B
【解析】
解：根据三角形的稳定性可得A、C、D都具有稳定性，不具有稳定性的是B选项．
故选：B．
4．（2019·山西省初一月考）如图是一座通信塔的一部分，可以看到它由三角形结构组成，其应用的数学原理是：_____________________．

【答案】三角形具有稳定性
【解析】
由于三角形具有稳定性，所以可用于通信塔的建设
故答案为：三角形具有稳定性．
5．（2019·内蒙古自治区初二期中）如图，李叔叔家的凳子坏了，于是他给凳子加了两根木条，这样凳子就比较牢固了，他所应用的数学原理是_____．

【答案】三角形的稳定性．
【解析】结合题意和图形，运用线段的性质、垂线的性质和三角形的稳定性解答．椅子加了两根木条，由图知，是构成三角形，所以根据三角形的稳定性．
故空中应填：三角形的稳定性．
考点6：三角形内角和
典例：（2019·河北省初一期末）已知△ABC中，BE平分∠ABC，点P在射线BE上．

（1）如图1，若∠ABC＝40°，CP∥AB，求∠BPC的度数；
（2）如图2，若∠BAC＝100°，∠PBC＝∠PCA，求∠BPC的度数；
（3）若∠ABC＝40°，∠ACB＝30°，直线CP与△ABC的一条边垂直，画出相应图形并求∠BPC的度数．
【答案】（1）∠BPC＝20°；（2）∠BPC=100°；（3）画出相应图形见解析；∠BPC的度数为70°或40°或110°．
【解析】
（1）∵BE平分∠ABC，∠ABC＝40°，
∴∠ABP＝＝20°，
∵CP∥AB，
∴∠BPC＝∠ABP＝20°；
（2）∵BE平分∠ABC，∠PBC＝∠PCA
∴∠ABP＝∠PBC＝∠PCA
△ABO中，∠A+∠ABP+∠AOB＝180°，
△PCO中，∠BPC+∠PCA+∠POC＝180°，
∵∠ABP=∠PCA, ∠AOB=∠POC
∴∠A＝∠BPC =100°
即∠BPC=100°；
（3）①当CP⊥BC时，如图3，则∠BCP＝90°，
∵∠PBC＝20°，
∴∠BPC＝70°；
②当CP⊥AC时，如图4，则∠ACP＝90°，
△BCP中，∠BPC＝180°﹣20°﹣30°﹣90°＝40°；
③当CP⊥AB时，延长CP交直线AB于G，如图5，则∠BGC＝90°，
∵∠ABC＝40°，
∴∠BCG＝50°
△BPC中，∠BPC＝180°﹣50°﹣20°＝110°；
综上，∠BPC的度数为70°或40°或110°．

方法或规律点拨
本题主要考查三角形的内角和定理，角平分线的定义，熟练掌握三角形内角和等于180°，是解题的关键．
巩固练习
1．（2020·隆昌市知行中学初三月考）如图，直线a∥b，点B在a上，且AB⊥BC，若∠1＝35°，那么∠2等于（ ）

A．45° B．50° C．55° D．60°
【答案】C
【解析】
解：∵直线a∥b，
∴∠BAC=∠1＝35°（两直线平行，内错角相等），
又∵AB⊥BC，
∴∠ABC=90°，
∴ （三角形内角和定理），
∴（对顶角相等），
故选：C．
2．（2020·河北省初一月考）一个最小的锐角是50°，这个三角形一定是（　　）
A．直角三角形 B．锐角三角形 C．钝角三角形 D．等腰三角形
【答案】B
【解析】180°﹣50°=130°，
另外两个角的和是130°，最小的内角是50°，
假设另外两个角中还有一个是50°，另一个就是：130°﹣50°=80°，
最大的内角最大只能是80°，所以这个三角形的三个角都是锐角，这个三角形一定是锐角三角形，
故选B．
3．（2020·江阴市云亭中学初一月考）若△ABC内有一个点P1，当P1、A、B、C没有任何三点在同一直线上时，如图1，可构成3个互不重叠的小三角形；若△ABC内有两个点P1、P2，其它条件不变，如图2，可构成5个互不重叠的小三角形：……若△ABC内有n个点，其它条件不变，则构成若干个互不重叠的小三角形，这些小三角形的内角和为（）

A．n·180° B．（n+2）·180° C．（2n-1）·180° D．（2n+1）·180°
【答案】D
【解析】解：图1中，当△ABC内只有1个点时，可分割成3个互不重叠的小三角形；
图2中，当△ABC内只有2个点时，可分割成5个互不重叠的小三角形；
图3中，当△ABC内只有3个点时，可分割成7个互不重叠的小三角形；
根据以上规律，当△ABC内有n个点（P1，P2，…，Pn）时，可以把△ABC分割成S=2n+1个互不重叠的三角形，所以这些小三角形的内角和为（2n+1）·180°.
4．（2020·广西壮族自治区初三其他）如图，AB∥CD，点E在线段BC上，CD=CE,若∠ABC=30°，则∠D为（　　）

A．85° B．75° C．60° D．30°
【答案】B
【解析】解：∵AB∥CD，
∴∠C=∠ABC=30°，
又∵CD=CE，
∴∠D=∠CED，
∵∠C+∠D+∠CED=180°，即30°+2∠D=180°，
∴∠D=75°．
故选B．
5．（2020·广东华侨中学初三其他）如图，直线AD∥BC，若∠1＝40°，∠BAC＝80°，则∠2的度数为（　　）

A．70° B．60° C．50° D．40°
【答案】B
【解析】
解：∵∠1＝40°，∠BAC＝80°，
∴∠ABC＝60°，
又∵AD∥BC，
∴∠2＝∠ABC＝60°，
故选：B．
6．（2020·山东省初三一模）在中，若一个内角等于另外两个角的差，则（ ）
A．必有一个角等于 B．必有一个角等于
C．必有一个角等于 D．必有一个角等于
【答案】D
【解析】
设三角形的一个内角为x，另一个角为y，则三个角为(180°－x－y)，则有三种情况：
①
②
③
综上所述，必有一个角等于90°
故选D.
7．（2019·四川省南充市高坪中学初一期末）如图，已知AM∥BN，∠A=60°．点P是射线AM上一动点（与点A不重合），BC、BD分别平分∠ABP和∠PBN，分别交射线AM于点C，D．
（1）求∠CBD的度数；
（2）当点P运动时，∠APB与∠ADB之间的数量关系是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由；若变化，请写出变化规律．
（3）当点P运动到使∠ACB=∠ABD时，直接写出∠ABC的度数．

【答案】（1）60°；（2）不变化，∠APB=2∠ADB ，理由详见解析；（3）∠ABC=30°
【解析】
解：（1）∵AM∥BN，
∴∠A+∠ABN=180°，　
∵∠A=60°
∴∠ABN=120°
∵BC、BD分别平分∠ABP和∠PBN，
∴∠CBP=∠ABP, ∠DBP=∠NBP,
∴∠CBD=∠CBP +∠DBP=∠ABN=60°
（2）不变化，∠APB=2∠ADB，理由：
∵AM∥BN，
∴∠APB=∠PBN
∠ADB=∠DBN
又∵BD平分∠PBN，
∴∠PBN =2∠DBN
∴∠APB=2∠ADB
（3）在△ABC中，∠A+∠ACB+∠ABC=180°，
在△ABD中，∠A+∠ABD+∠ADB=180°，
∵∠ACB=∠ABD,∴∠ABC=∠ADB
∵AD∥BN，∠A=60°，
∴∠ABN=120°，∠ADB=∠DBN=∠ABC，
由（1）知∠CBD=60°，
∴∠ABC=(∠ABN-∠CBD)=30°