2021年湖南省湘潭市九年级下学期期中数学试卷（有答案）

这是一份2021年湖南省湘潭市九年级下学期期中数学试卷（有答案），共25页。试卷主要包含了单项选择题，填空题，解答题等内容，欢迎下载使用。

2020-2021学年湖南省湘潭市九年级（下）期中数学试卷
一、单项选择题（本大题共8小题，每小题有且只有一个正确答案，请将正确答案的选项代号涂在答题卡相应的位置上，每小题3分，满分24分）
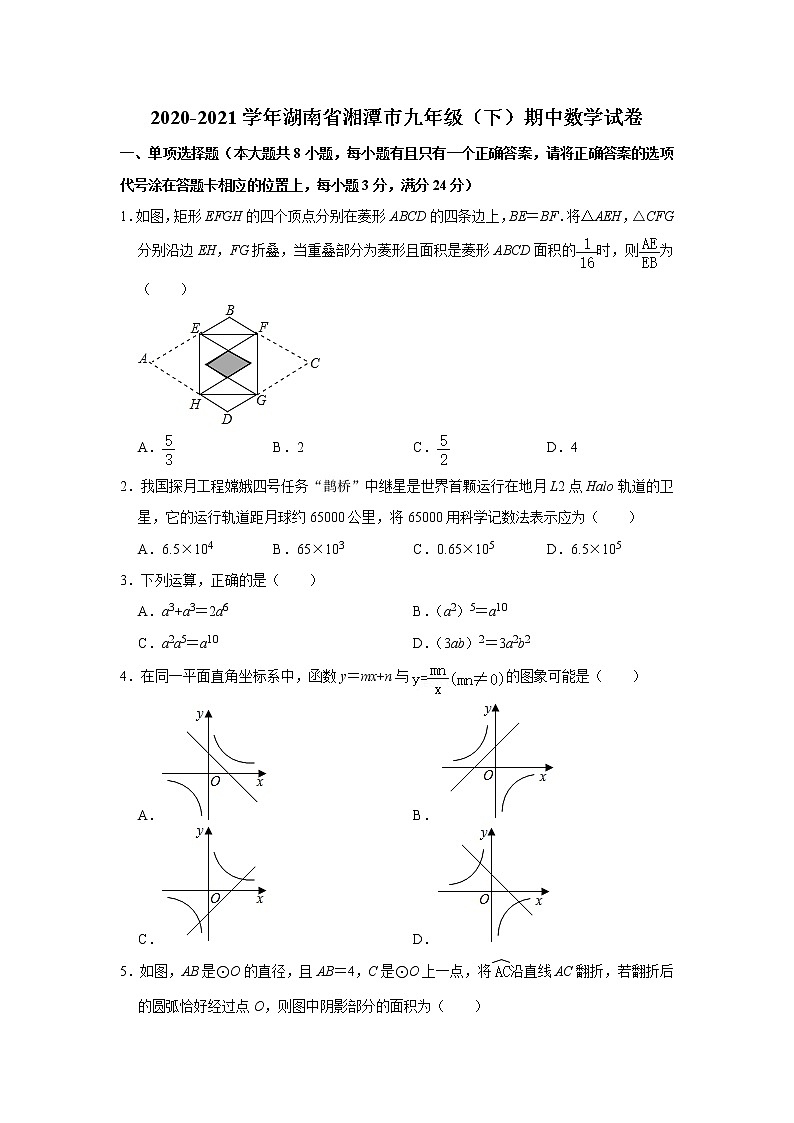
1．如图，矩形EFGH的四个顶点分别在菱形ABCD的四条边上，BE＝BF．将△AEH，△CFG分别沿边EH，FG折叠，当重叠部分为菱形且面积是菱形ABCD面积的时，则为（　　）

A． B．2 C． D．4
2．我国探月工程嫦娥四号任务“鹊桥”中继星是世界首颗运行在地月L2点Halo轨道的卫星，它的运行轨道距月球约65000公里，将65000用科学记数法表示应为（　　）
A．6.5×104 B．65×103 C．0.65×105 D．6.5×105
3．下列运算，正确的是（　　）
A．a3+a3＝2a6 B．（a2）5＝a10
C．a2a5＝a10 D．（3ab）2＝3a2b2
4．在同一平面直角坐标系中，函数y＝mx+n与的图象可能是（　　）
A． B．
C． D．
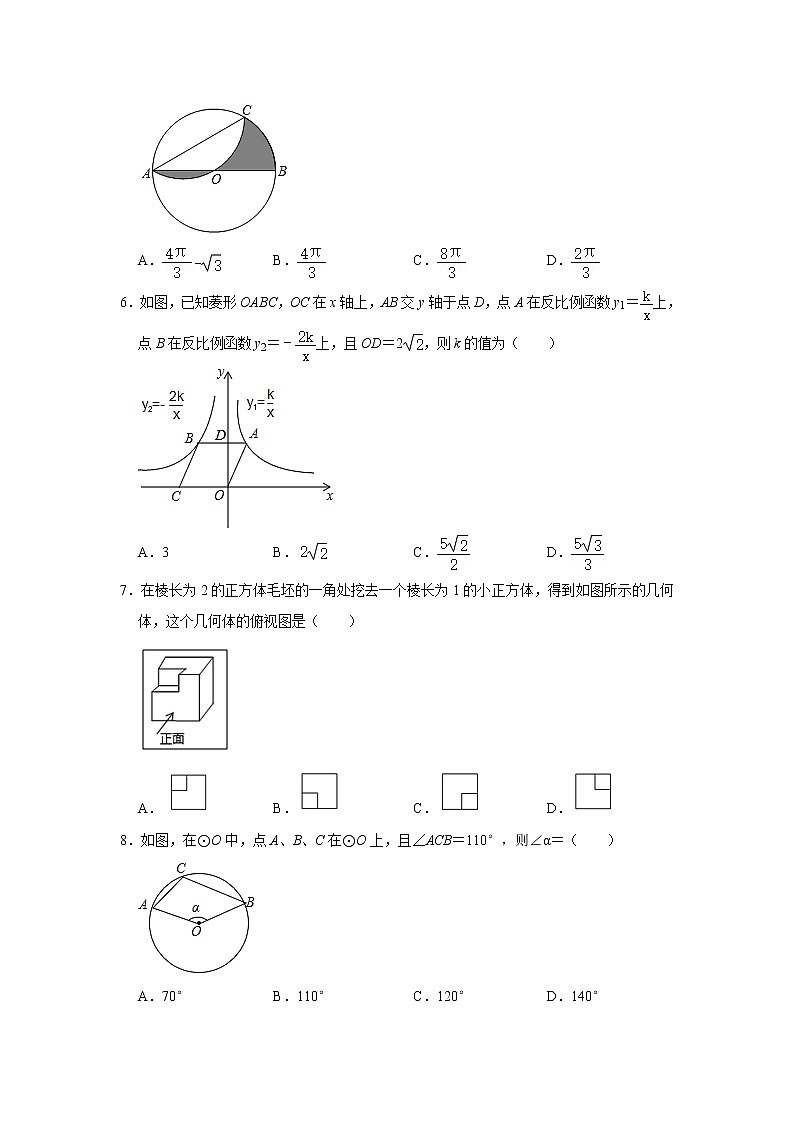
5．如图，AB是⊙O的直径，且AB＝4，C是⊙O上一点，将沿直线AC翻折，若翻折后的圆弧恰好经过点O，则图中阴影部分的面积为（　　）

A． B． C． D．
6．如图，已知菱形OABC，OC在x轴上，AB交y轴于点D，点A在反比例函数y1＝上，点B在反比例函数y2＝﹣上，且OD＝2，则k的值为（　　）

A．3 B． C． D．
7．在棱长为2的正方体毛坯的一角处挖去一个棱长为1的小正方体，得到如图所示的几何体，这个几何体的俯视图是（　　）

A． B． C． D．
8．如图，在⊙O中，点A、B、C在⊙O上，且∠ACB＝110°，则∠α＝（　　）

A．70° B．110° C．120° D．140°
二、填空题（本大题共8小题，请将答案填写在相应位置，每小题3分，共24分）
9．开学前，根据学校防疫要求，小明同学连续14天进行了体温测量，结果统计如下表：
体温（℃）
36.3
36.4
36.5
36.6
36.7
36.8
天数（天）
2
3
3
4
1
1
这组体温数据的中位数是　 　℃．

10．如图，在平行四边形ABCD中，AB＝8，BC＝10，∠ABC＝60°，BE平分∠ABC交AD于点E，AF平分∠BAD交BC于点F，交BE于点G，连接DG，则GD的长为　 　．

11．已知实数a、b、c满足a+b＝ab＝c，有下列结论：
①若c≠0，则+＝1；
②若a＝3，则b+c＝9；
③若a＝b＝c，则abc＝0；
④若a、b、c中只有两个数相等，则a+b+c＝8．
其中正确的是　 　（把所有正确结论的序号都选上）．
12．要使式子有意义，则字母x的取值范围是　 　．
13．如图，Rt△ABC中，∠C＝90o，∠A＝30o，BC＝1，以点B为圆心，以BC长度为半径作弧，交BA于点D，以点C为圆心，以大于为半径作弧，接着再以点D为圆心，以相同长度为半径作弧，两弧交于点E，作射线BE交CA于点F，以点B为圆心，以BF为长度作弧，交BA于点G，则阴影部分的面积为　 　．

14．在一个不透明的布袋中，装有红、黑、白三种只有颜色不同的小球，其中红色小球4个，黑、白色小球的数目相同．小明从布袋中随机摸出一球，记下颜色后放回布袋中，摇匀后随机摸出一球，记下颜色；…如此大量摸球实验后，小明发现其中摸出的红球的频率稳定于20%，由此可以估计布袋中的黑色小球有　 　个．
15．分解因式：2a2﹣2＝　 　．
16．如图，已知在△ABC中，AB＝AC，点D，E在BC上，且BD＝CE，请你在图中找出一组全等三角形　 　．（不添加任何字母和辅助线）

三、解答题（本大题共8小题，共72分）
17．（6分）计算：．
18．（6分）先化简，再求值：÷（1+），其中x＝+1．
19．（6分）“校园安全”受到全社会的广泛关注，我市某中学对部分学生就校园安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了如图两幅尚不完整的统计图，请你根据统计图中所提供的的信息解答下列问题：
（1）接受问卷调查的学生共有　 　人，扇形统计图中“了解”部分所对应的扇形的圆心角的度数为　 　°；
（2）若该中学共有学生900人，请根据上述调查结果，估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为多少人？

20．（10分）如图，AC是⊙O的直径，OD与⊙O相交于点B，∠DAB＝∠ACB．
（1）求证：AD是⊙O的切线．
（2）若∠ADB＝30°，DB＝2，求直径AC的长度．

21．（8分）如图，某中学有一块三角形状的花圃ABC，现可直接测量到∠B＝45°，∠C＝30°，AC＝8米．请你求出BC的长．（结果可保留根号）

22．（12分）如图，直线y＝x+2与抛物线y＝ax2+bx+6（a≠0）相交于A（，）和B（4，m），点P是线段AB上异于A、B的动点，过点P作PC⊥x轴于点D，交抛物线于点C．
（1）求抛物线的解析式；
（2）是否存在这样的P点，使线段PC的长有最大值？若存在，求出这个最大值；若不存在，请说明理由；
（3）求△PAC为直角三角形时点P的坐标．

23．（12分）如图，AB、AC为⊙O的弦，连接CO、BO并延长分别交弦AB、AC于点E、F，∠B＝∠C．
求证：CE＝BF．

24．（12分）在平面直角坐标系中，已知A（﹣3，0），B（0，3），点C为x轴正半轴上一动点，过点A作AD⊥BC交y轴于点E．

（1）如图①，若点C的坐标为（2，0），试求点E的坐标；
（2）如图②，若点C在x正半轴上运动，且OC＜3，其它条件不变，连接OD，求证：OD平分∠ADC；
（3）若点C在x轴正半轴上运动，当AD﹣CD＝OC时，求∠OCD的度数．

2020-2021学年湖南省湘潭市九年级（下）期中数学试卷
参考答案与试题解析
一、单项选择题（本大题共8小题，每小题有且只有一个正确答案，请将正确答案的选项代号涂在答题卡相应的位置上，每小题3分，满分24分）
1．如图，矩形EFGH的四个顶点分别在菱形ABCD的四条边上，BE＝BF．将△AEH，△CFG分别沿边EH，FG折叠，当重叠部分为菱形且面积是菱形ABCD面积的时，则为（　　）

A． B．2 C． D．4
【分析】设重叠的菱形边长为x，BE＝BF＝y，由矩形和菱形的对称性以及折叠的性质得：四边形AHME、四边形BENF是菱形，得出EN＝BE＝y，EM＝x+y，由相似的性质得出AB＝4MN＝4x，求出AE＝AB﹣BE＝4x﹣y，得出方程4x﹣y＝x+y，得出x＝y，AE＝y，即可得出结论．
【解答】解：设重叠的菱形边长为x，BE＝BF＝y，
由矩形和菱形的对称性以及折叠的性质得：四边形AHME、四边形BENF是菱形，
∴AE＝EM，EN＝BE＝y，EM＝x+y，
∵当重叠部分为菱形且面积是菱形ABCD面积的，且两个菱形相似，
∴AB＝4MN＝4x，
∴AE＝AB﹣BE＝4x﹣y，
∴4x﹣y＝x+y，
解得：x＝y，
∴AE＝y，
∴＝＝；
故选：A．

2．我国探月工程嫦娥四号任务“鹊桥”中继星是世界首颗运行在地月L2点Halo轨道的卫星，它的运行轨道距月球约65000公里，将65000用科学记数法表示应为（　　）
A．6.5×104 B．65×103 C．0.65×105 D．6.5×105
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正数；当原数的绝对值＜1时，n是负数．
【解答】解：将65000用科学记数法表示为：6.5×104．
故选：A．
3．下列运算，正确的是（　　）
A．a3+a3＝2a6 B．（a2）5＝a10
C．a2a5＝a10 D．（3ab）2＝3a2b2
【分析】根据合并同类项、幂的乘方、同底数幂的乘法、积的乘方法则来分析．
【解答】解：
A．错误，a3+a3＝2a3
B．正确，因为幂的乘方，底数不变，指数相乘．
C．错误，a2a5＝a7
D．错误，（3ab）2＝9a2b2
故选：B．
4．在同一平面直角坐标系中，函数y＝mx+n与的图象可能是（　　）
A． B．
C． D．
【分析】根据一次函数的性质和反比例函数的性质，可以判断各个选项中的图象是否正确．
【解答】解：当m＜0，n＞0时，函数y＝mx+n的图象经过第一、二、四象限，的图象在第二、四象限，故选项A错误、选项D正确；
当m＞0，n＞0时，函数y＝mx+n的图象经过第一、二、三象限，的图象在第一、三象限，故选项B错误；
当m＞0，n＜0时，函数y＝mx+n的图象经过第一、三、四象限，的图象在第二、四象限，故选项C错误；
故选：D．
5．如图，AB是⊙O的直径，且AB＝4，C是⊙O上一点，将沿直线AC翻折，若翻折后的圆弧恰好经过点O，则图中阴影部分的面积为（　　）

A． B． C． D．
【分析】根据题意和图形，可知阴影部分的面积＝扇形BOC的面积，然后根据题目中的数据，计算出扇形BOC的面积即可．
【解答】解：连接OC，作OD⊥AC于点D，
由图可知，阴影部分的面积＝扇形BOC的面积，
∵OD＝OC，∠ODC＝90°，AB＝4，
∴∠DCO＝30°，OC＝2，
∵OA＝OC，
∴∠OAC＝∠OCA＝30°，
∴∠BOC＝60°，
∴扇形BOC的面积是：＝π，
故选：D．

6．如图，已知菱形OABC，OC在x轴上，AB交y轴于点D，点A在反比例函数y1＝上，点B在反比例函数y2＝﹣上，且OD＝2，则k的值为（　　）

A．3 B． C． D．
【分析】估计菱形的性质得到AB∥OC，求得AB⊥y轴，得到A（，2），B（﹣，2），求得AB＝，AD＝，根据勾股定理即可得到结论．
【解答】解：∵四边形ABCO是菱形，
∴AB∥OC，
∴AB⊥y轴，
∵OD＝2，
∴A（，2），B（﹣，2），
∴AB＝，AD＝，
∵AB＝OA，
∴OA＝，
∵AD2+OD2＝OA2，
∴（）2+（2）2＝（）2，
∴k＝2，
故选：B．
7．在棱长为2的正方体毛坯的一角处挖去一个棱长为1的小正方体，得到如图所示的几何体，这个几何体的俯视图是（　　）

A． B． C． D．
【分析】根据从上边看得到的图形是俯视图，可得答案．
【解答】解：从上边看，是一个正方形，正方形的左下角是一个小正方形，
故选：B．
8．如图，在⊙O中，点A、B、C在⊙O上，且∠ACB＝110°，则∠α＝（　　）

A．70° B．110° C．120° D．140°
【分析】作所对的圆周角∠ADB，如图，利用圆内接四边形的性质得∠ADB＝70°，然后根据圆周角定理求解．
【解答】解：作所对的圆周角∠ADB，如图，
∵∠ACB+∠ADB＝180°，
∴∠ADB＝180°﹣110°＝70°，
∴∠AOB＝2∠ADB＝140°．
故选：D．

二、填空题（本大题共8小题，请将答案填写在相应位置，每小题3分，共24分）
9．开学前，根据学校防疫要求，小明同学连续14天进行了体温测量，结果统计如下表：
体温（℃）
36.3
36.4
36.5
36.6
36.7
36.8
天数（天）
2
3
3
4
1
1
这组体温数据的中位数是　36.5　℃．

【分析】根据中位数的定义求解即可．
【解答】解：∵共有14个数据，其中位数是第7、8个数据的平均数，而第7、8个数据均为36.5，
∴这组体温数据的中位数是＝36.5（℃），
故答案为：36.5．
10．如图，在平行四边形ABCD中，AB＝8，BC＝10，∠ABC＝60°，BE平分∠ABC交AD于点E，AF平分∠BAD交BC于点F，交BE于点G，连接DG，则GD的长为　　．

【分析】过点G作GH⊥AD于点H，由平行四边形的性质得出AD∥BC，证明△ABF为等边三角形，由等腰三角形的性质得出AG＝4，由直角三角形的性质得出AH＝2，由勾股定理可求出答案．
【解答】解：过点G作GH⊥AD于点H，

∵四边形ABCD是平行四边形，
∴AD∥BC，
∵∠ABC＝60°，
∴∠BAD＝120°，
∵AF平分∠BAD，
∴∠BAF＝∠DAF＝∠AFB＝60°，
∴△ABF为等边三角形，AB＝AF＝8，
∵BE平分∠ABC，
∴AG＝GF＝4，
又∵∠AHG＝90°，
∴∠AGH＝30°，
∴AH＝AG＝2，GH＝2，
∴DH＝AD﹣AH＝10﹣2＝8，
∴DG＝＝＝2，
故答案为：2．
11．已知实数a、b、c满足a+b＝ab＝c，有下列结论：
①若c≠0，则+＝1；
②若a＝3，则b+c＝9；
③若a＝b＝c，则abc＝0；
④若a、b、c中只有两个数相等，则a+b+c＝8．
其中正确的是　①③④　（把所有正确结论的序号都选上）．
【分析】按照字母满足的条件，逐一分析计算得出答案，进一步比较得出结论即可．
【解答】解：①∵a+b＝ab＝c≠0，∴+＝1，此选项正确；
②∵a＝3，则3+b＝3b，b＝，c＝，∴b+c＝+＝6，此选项错误；
③∵a＝b＝c，则2a＝a2＝a，∴a＝0，abc＝0，此选项正确；
④∵a、b、c中只有两个数相等，不妨a＝b，则2a＝a2，a＝0，或a＝2，a＝0不合题意，a＝2，则b＝2，c＝4，∴a+b+c＝8．当a＝c时，则b＝0，不符合题意，b＝c时，a＝0，此时a+b＝ab＝c＝0，b＝c＝0，也不符合题意；
故只能是a＝b＝2，c＝4；此选项正确
其中正确的是①③④．
故答案为：①③④．
12．要使式子有意义，则字母x的取值范围是　x＞2　．
【分析】求二次根式中被开方数的取值范围，依据为二次根式中的被开方数是非负数．
【解答】解：要使式子有意义，则x﹣2＞0，
解得x＞2，
∴字母x的取值范围是x＞2，
故答案为：x＞2．
13．如图，Rt△ABC中，∠C＝90o，∠A＝30o，BC＝1，以点B为圆心，以BC长度为半径作弧，交BA于点D，以点C为圆心，以大于为半径作弧，接着再以点D为圆心，以相同长度为半径作弧，两弧交于点E，作射线BE交CA于点F，以点B为圆心，以BF为长度作弧，交BA于点G，则阴影部分的面积为　﹣　．

【分析】根据S阴＝S△ABF﹣S△BGF，求解即可．
【解答】解：由作图可知，BE平分∠ABC，
∵∠C＝90°，∠A＝30°，
∴∠CBA＝90°﹣30°＝60°，
∴∠CBF＝∠FBA＝30°，
∵BC＝1，
∴CF＝BC•tan30°＝，AC＝BC•tan60°＝，BF＝2CF＝，
∴S阴＝S△ABF﹣S△BGF＝××1﹣＝﹣，
故答案为：﹣．
14．在一个不透明的布袋中，装有红、黑、白三种只有颜色不同的小球，其中红色小球4个，黑、白色小球的数目相同．小明从布袋中随机摸出一球，记下颜色后放回布袋中，摇匀后随机摸出一球，记下颜色；…如此大量摸球实验后，小明发现其中摸出的红球的频率稳定于20%，由此可以估计布袋中的黑色小球有　8　个．
【分析】根据多次试验发现摸到红球的频率是20%，则可以得出摸到红球的概率为20%，再利用红色小球有4个，黄、白色小球的数目相同进而表示出黑球概率，得出答案即可．
【解答】解：设黑色的数目为x，则黑、白色小球一共有2x个，
∵多次试验发现摸到红球的频率是20%，则得出摸到红球的概率为20%，
∴＝20%，解得：x＝8，
∴黑色小球的数目是8个．
故答案为：8．
15．分解因式：2a2﹣2＝　2（a+1）（a﹣1）　．
【分析】先提取公因式2，再对余下的多项式利用平方差公式继续分解．
【解答】解：2a2﹣2，
＝2（a2﹣1），
＝2（a+1）（a﹣1）．
16．如图，已知在△ABC中，AB＝AC，点D，E在BC上，且BD＝CE，请你在图中找出一组全等三角形　△ABD≌△ACE或△ABE≌△ACD　．（不添加任何字母和辅助线）

【分析】首先根据等腰三角形的性质：等角对等边得出∠B＝∠C，然后根据SAS证明△ABD≌△ACE，△ABE≌△ACD，则图中全等的三角形共有2对．
【解答】解：在△ABD与△ACE中，
，
∴△ABD≌△ACE（SAS）；
∵BD＝CE，
∴BD+DE＝CE+DE，
∴BE＝CD．
在△ABD与△ACD中，
，
∴△ABE≌△ACD（SAS）；
故答案为：△ABD≌△ACE或△ABE≌△ACD．
三、解答题（本大题共8小题，共72分）
17．（6分）计算：．
【分析】直接利用零指数幂的性质以及二次根式的性质、绝对值的性质、负整数指数幂的性质分别化简得出答案．
【解答】解：原式＝1+4﹣2×
＝1+4﹣
＝．
18．（6分）先化简，再求值：÷（1+），其中x＝+1．
【分析】根据分式的运算法则即可求出答案．
【解答】解：原式＝•
＝
当x＝+1时，
原式＝
＝
19．（6分）“校园安全”受到全社会的广泛关注，我市某中学对部分学生就校园安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了如图两幅尚不完整的统计图，请你根据统计图中所提供的的信息解答下列问题：
（1）接受问卷调查的学生共有　60　人，扇形统计图中“了解”部分所对应的扇形的圆心角的度数为　30　°；
（2）若该中学共有学生900人，请根据上述调查结果，估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为多少人？

【分析】（1）从两个统计图中可知“了解很少”的频数为30人，占调查人数的50%，可求出调查人数，进而求出“了解”的频数、所占得百分比，相应的圆心角的度数；
（2）求出“了解”“基本了解”所占得百分比即可求出答案．
【解答】解：（1）接受问卷调查的人数为：30÷50%＝60（人），
“了解”的人数为：60﹣15﹣30﹣10＝5（人），
所以扇形统计图中“了解”部分所对应的扇形的圆心角的度数为：360°×＝30°，
故答案为：60，30；
（2）“了解”和“基本了解”的人数为15+5＝20（人），
因此整体中，达到“了解”和“基本了解”的人数为：900×＝300（人），
答：该中学900中对校园安全知识达到“了解”和“基本了解”的共有300人．
20．（10分）如图，AC是⊙O的直径，OD与⊙O相交于点B，∠DAB＝∠ACB．
（1）求证：AD是⊙O的切线．
（2）若∠ADB＝30°，DB＝2，求直径AC的长度．

【分析】（1）根据圆周角定理得出∠ABC＝90°，求出∠ACB+∠CAB＝90°，求出∠OAD＝90°，再根据切线的判定得出即可；
（2）根据含30°角的直角三角形的性质得出OA＝OD，求出OA，再求出答案即可．
【解答】（1）证明：∵AC是⊙O的直径，
∴∠ABC＝90°，
∴∠ACB+∠CAB＝90°，
又∵∠ACB＝∠DAB，
∴∠DAB+∠CAB＝90°，即∠OAD＝90°，
∵OA是⊙O的半径，
∴AD是⊙O的切线；

（2）解：由（1）可知∠OAD＝90°，
∵∠ADB＝30°，
∴OA＝OD＝（OB+BD），
∵OA＝OB，BD＝2，
∴OA＝2，
∴AC＝2OA＝4．
21．（8分）如图，某中学有一块三角形状的花圃ABC，现可直接测量到∠B＝45°，∠C＝30°，AC＝8米．请你求出BC的长．（结果可保留根号）

【分析】直接过A作AD⊥BC于D，分别得出BD，DC的长进而得出答案．
【解答】解：如图：过A作AD⊥BC于D．
在△ABD中，∵∠B＝45°，
∴AD＝BD．在△ACD中，
∵∠C＝30°，AC＝8，
∴AD＝AC＝4＝BD，
∴CD＝＝4，
∴BC＝BD+CD＝4+4，
答：BC的长为：（4+4）m．

22．（12分）如图，直线y＝x+2与抛物线y＝ax2+bx+6（a≠0）相交于A（，）和B（4，m），点P是线段AB上异于A、B的动点，过点P作PC⊥x轴于点D，交抛物线于点C．
（1）求抛物线的解析式；
（2）是否存在这样的P点，使线段PC的长有最大值？若存在，求出这个最大值；若不存在，请说明理由；
（3）求△PAC为直角三角形时点P的坐标．

【分析】（1）已知B（4，m）在直线y＝x+2上，可求得m的值，抛物线图象上的A、B两点坐标，可将其代入抛物线的解析式中，通过联立方程组即可求得待定系数的值．
（2）要弄清PC的长，实际是直线AB与抛物线函数值的差．可设出P点横坐标，根据直线AB和抛物线的解析式表示出P、C的纵坐标，进而得到关于PC与P点横坐标的函数关系式，根据函数的性质即可求出PC的最大值．
（3）当△PAC为直角三角形时，根据直角顶点的不同，有三种情形，需要分类讨论，分别求解．
【解答】解：（1）∵B（4，m）在直线y＝x+2上，
∴m＝4+2＝6，
∴B（4，6），
∵A（，）、B（4，6）在抛物线y＝ax2+bx+6上，
∴，解得，
∴抛物线的解析式为y＝2x2﹣8x+6．

（2）设动点P的坐标为（n，n+2），则C点的坐标为（n，2n2﹣8n+6），
∴PC＝（n+2）﹣（2n2﹣8n+6），
＝﹣2n2+9n﹣4，
＝﹣2（n﹣）2+，
∵PC＞0，
∴当n＝时，线段PC最大且为．

（3）∵△PAC为直角三角形，
i）若点P为直角顶点，则∠APC＝90°．
由题意易知，PC∥y轴，∠APC＝45°，因此这种情形不存在；
ii）若点A为直角顶点，则∠PAC＝90°．
如答图3﹣1，过点A（，）作AN⊥x轴于点N，则ON＝，AN＝．
过点A作AM⊥直线AB，交x轴于点M，则由题意易知，△AMN为等腰直角三角形，
∴MN＝AN＝，∴OM＝ON+MN＝+＝3，
∴M（3，0）．
设直线AM的解析式为：y＝kx+b，
则：，解得，
∴直线AM的解析式为：y＝﹣x+3 ①
又抛物线的解析式为：y＝2x2﹣8x+6 ②
联立①②式，解得：x＝3或x＝（与点A重合，舍去）
∴C（3，0），即点C、M点重合．
当x＝3时，y＝x+2＝5，
∴P1（3，5）；

iii）若点C为直角顶点，则∠ACP＝90°．
∵y＝2x2﹣8x+6＝2（x﹣2）2﹣2，
∴抛物线的对称轴为直线x＝2．
如答图3﹣2，作点A（，）关于对称轴x＝2的对称点C，
则点C在抛物线上，且C（，）．
当x＝时，y＝x+2＝．
∴P2（，）．
∵点P1（3，5）、P2（，）均在线段AB上，
∴综上所述，△PAC为直角三角形时，点P的坐标为（3，5）或（，）．
23．（12分）如图，AB、AC为⊙O的弦，连接CO、BO并延长分别交弦AB、AC于点E、F，∠B＝∠C．
求证：CE＝BF．

【分析】因为OB，OC是⊙O的半径，所以OB＝OC，又因为∠B＝∠C，∠BOE＝∠COF，易证△EOB≌△FOC，则可求证CE＝BF．
【解答】证明：∵OB，OC是⊙O的半径，
∴OB＝OC．
又∵∠B＝∠C，∠BOE＝∠COF，
∴△EOB≌△FOC（ASA）．
∴OE＝OF．
∵CE＝OC+OE，BF＝OB+OF，
∴CE＝BF．
24．（12分）在平面直角坐标系中，已知A（﹣3，0），B（0，3），点C为x轴正半轴上一动点，过点A作AD⊥BC交y轴于点E．

（1）如图①，若点C的坐标为（2，0），试求点E的坐标；
（2）如图②，若点C在x正半轴上运动，且OC＜3，其它条件不变，连接OD，求证：OD平分∠ADC；
（3）若点C在x轴正半轴上运动，当AD﹣CD＝OC时，求∠OCD的度数．
【分析】（1）证明△AOE≌△BOC（ASA），可得结论．
（2）如图②，过点O作OM⊥AD于点M，作ON⊥BC于点N，证明OM＝ON，可得结论．
（3）如图所示，在DA上截取DP＝DC，连接OP，证明△OPD≌△OCD（SAS），可得结论．
【解答】（1）解：如图①，

∵AD⊥BC，BO⊥AO，
∴∠AOE＝∠BDE＝90°，
又∵∠AEO＝∠BED，
∴∠OAE＝∠OBC，
∵A（﹣3，0），B（0，3），
∴OA＝OB＝3，
在△AOE和△BOC中，
，
∴△AOE≌△BOC（ASA），
∴OE＝OC，
又∵点C的坐标为（2，0），
∴OC＝2＝OE，
∴点E的坐标为（0，2）．

（2）证明：如图②，过点O作OM⊥AD于点M，作ON⊥BC于点N，

∵△AOE≌△BOC，
∴S△AOE＝S△BOC，且AE＝BC，
∵OM⊥AE，ON⊥BC，
∴OM＝ON，
∴OD平分∠ADC．

（3）解：如图所示，在DA上截取DP＝DC，连接OP，

∵∠PDO＝∠CDO，OD＝OD，
在△OPD和△OCD中，
，
∴△OPD≌△OCD（SAS），
∴OC＝OP，∠OPD＝∠OCD，
∵AD﹣CD＝OC，
∴AD﹣DP＝OP，即AP＝OP，
∴∠PAO＝∠POA，
∴∠OPD＝∠PAO+∠POA＝2∠PAO＝∠OCB，
又∵∠PAO+∠OCD＝90°，
∴3∠PAO＝90°，
∴∠PAO＝30°，
∴∠OCD＝60°．