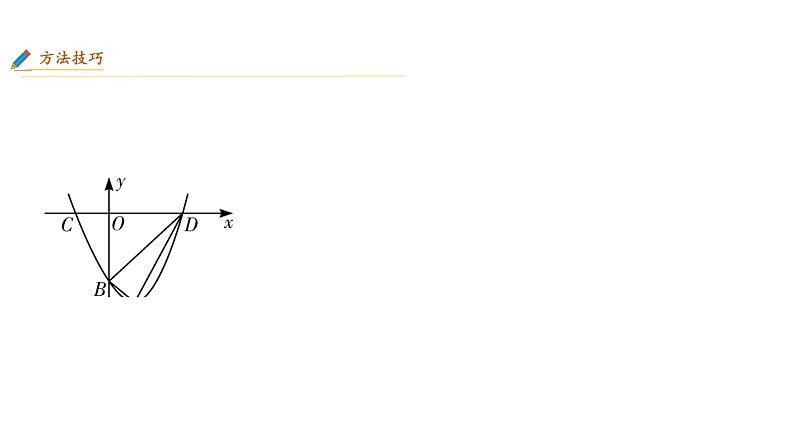
专题18 函数与线段、面积等最值问题【考点精讲】-【中考高分导航】备战2022年中考数学考点总复习（全国通用）课件PPT

1．二次函数与线段的和差

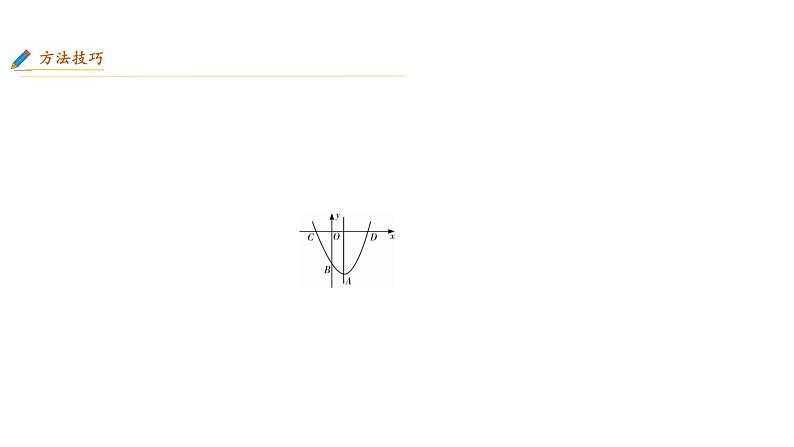
在x轴上是否存在点P，使PB+PA最短？若存在求出点P的坐标，并求出最小值。若不存在，请说明理由。

【方法技巧】（将军饮马模型）在两定点中任选一个点(为了简单起见，常常取轴上的点)，求出该点关于题中的动点运动所经过的那条直线的对称点的坐标，再把此对称点与余下定点相连，那么此直线与在x轴上的交点既是点P。

2．二次函数与周长

在y轴上是否存在点P，使△PAD的周长最小？若存在，求出点P的坐标，并求出周长的最小值；若不存在，请说明理由。

注意到AD是定线段，其长度是个定值，因此只需PA+PD最小。

3．二次函数与距离

在直线BD下方的抛物线上，是否存在点P，使点P到直线BD的距离最大？若存在，求出点P的坐标，并求出最大距离；若不存在，请说明理由.

因为BD是定线段，点P到直线BD的距离最大，意味着△BDP的面积最大

4．二次函数与面积

① 三角形面积最值：找公共边、平移、表示面积

② 四边形面积最值：设出P点坐标，采用公式法或割补法表示四边形面积

（1）在直线BD下方的抛物线上是否存在点P，使的面积最大？若存在，求出点P的坐标；若不存在，请说明理由。

过点P作y轴的平行线，将△PBD分割成2个同底的三角形，则：(y上动-y下动)(x右定-x左定)

（2）在直线BD下方的抛物线上是否存在点P，使四边形DOBP的面积最大？若存在，求出点P的坐标，并求出四边形面积的最大值；若不存在，请说明理由。

四边形DOBP是不规则图形，通常用割补法求解，则：或

（3）在抛物线上是否存在点P，使S△PBC=2S△ABD？若存在，求出点P的坐标；若不存在，请说明理由。

设出动点P的坐标为(t,t2-2t-3)后，把到图形△ABD的面积算出，借助于动点坐标把动三角形PBC的面积表示出来，再代入已知中的面积等式求解即可。

题型一：函数与最值问题

【例1】（2021·山东）在平面直角坐标系中，抛物线的顶点为A．

（1）求顶点A的坐标（用含有字母m的代数式表示）；

（2）若点，在抛物线上，且，则m的取值范围是          ；（直接写出结果即可）

（3）当时，函数y的最小值等于6，求m的值．

题型二：函数与线段、周长问题

【例2】（2021·四川）如图1，在平面直角坐标系中，抛物线与x轴分别交于A、B两点，与y轴交于点C（0，6），抛物线的顶点坐标为E（2，8），连结BC、BE、CE．

（1）求抛物线的表达式；

（2）判断△BCE的形状，并说明理由；

（3）如图2，以C为圆心，为半径作⊙C，在⊙C上是否存在点P，使得BP＋EP的值最小，若存在，请求出最小值；若不存在，请说明理由．

【例3】（2021·黑龙江）如图，抛物线与轴交于除原点和点，且其顶点关于轴的对称点坐标为．

（1）求抛物线的函数表达式；

（2）抛物线的对称轴上存在定点，使得抛物线上的任意一点到定点的距离与点到直线的距离总相等．

①证明上述结论并求出点的坐标；

②过点的直线与抛物线交于两点．证明：当直线绕点旋转时，是定值，并求出该定值；

（3）点是该抛物线上的一点，在轴，轴上分别找点，使四边形周长最小，直接写出的坐标．

题型三：函数与三角形面积

【例4】（2021·湖南）如图，在平面直角坐标系中，平行四边形的边与y轴交于E点，F是的中点，B、C、D的坐标分别为．

（1）求过B、E、C三点的抛物线的解析式；

（2）试判断抛物线的顶点是否在直线上；

（3）设过F与平行的直线交y轴于Q，M是线段之间的动点，射线与抛物线交于另一点P，当的面积最大时，求P的坐标．

题型四：函数与四边形面积

【例5】（2021·四川）如图，抛物线与x轴交于A、B两点，与y轴交于C点，，．

（1）求抛物线的解析式；

（2）在第二象限内的抛物线上确定一点P，使四边形PBAC的面积最大．求出点P的坐标

（3）在（2）的结论下，点M为x轴上一动点，抛物线上是否存在一点Q．使点P、B、M、Q为顶点的四边形是平行四边形，若存在．请直接写出Q点的坐标；若不存在，请说明理由．

1．（2021·甘肃）如图，在平面直角坐标系中，抛物线与坐标轴交于两点，直线交轴于点．点为直线下方抛物线上一动点，过点作轴的垂线，垂足为分别交直线于点．

（1）求抛物线的表达式；

（2）当，连接，求的面积；

（3）①是轴上一点，当四边形是矩形时，求点的坐标；

②在①的条件下，第一象限有一动点，满足，求周长的最小值．

2．（2021·福建）已知抛物线与x轴只有一个公共点．

（1）若抛物线过点，求的最小值；

（2）已知点中恰有两点在抛物线上．

①求抛物线的解析式；

②设直线l：与抛物线交于M，N两点，点A在直线上，且，过点A且与x轴垂直的直线分别交抛物线和于点B，C．求证：与的面积相等．

3．（2020•衡阳）在平面直角坐标系xOy中，关于x的二次函数y＝x2+px+q的图象过点（﹣1，0），（2，0）．

（1）求这个二次函数的表达式；

（2）求当﹣2≤x≤1时，y的最大值与最小值的差；

（3）一次函数y＝（2﹣m）x+2﹣m的图象与二次函数y＝x2+px+q的图象交点的横坐标分别是a和b，且a＜3＜b，求m的取值范围．

4．（2021·天津）已知抛物线（a，c为常数，）经过点，顶点为D．

（Ⅰ）当时，求该抛物线的顶点坐标；

（Ⅱ）当时，点，若，求该抛物线的解析式；

（Ⅲ）当时，点，过点C作直线l平行于x轴，是x轴上的动点，是直线l上的动点．当a为何值时，的最小值为，并求此时点M，N的坐标．

5．（2021·江苏）如图，二次函数（是实数，且）的图像与轴交于、两点（点在点的左侧），其对称轴与轴交于点，已知点位于第一象限，且在对称轴上，，点在轴的正半轴上，．连接并延长交轴于点，连接．

（1）求、、三点的坐标（用数字或含的式子表示）；

（2）已知点在抛物线的对称轴上，当的周长的最小值等于，求的值．

6．（2020•凉山州）如图，二次函数y＝ax2+bx+x的图象过O（0，0）、A（1，0）、B（，）三点．

（1）求二次函数的解析式；

（2）若线段OB的垂直平分线与y轴交于点C，与二次函数的图象在x轴上方的部分相交于点D，求直线CD的解析式；

（3）在直线CD下方的二次函数的图象上有一动点P，过点P作PQ⊥x轴，交直线CD于Q，当线段PQ的长最大时，求点P的坐标．

7．（2020•杭州）在平面直角坐标系中，设二次函数y1＝x2+bx+a，y2＝ax2+bx+1（a，b是实数，a≠0）．

（1）若函数y1的对称轴为直线x＝3，且函数y1的图象经过点（a，b），求函数y1的表达式．

（2）若函数y1的图象经过点（r，0），其中r≠0，求证：函数y2的图象经过点（，0）．

（3）设函数y1和函数y2的最小值分别为m和n，若m+n＝0，求m，n的值．

8．（2020•安徽）在平面直角坐标系中，已知点A（1，2），B（2，3），C（2，1），直线y＝x+m经过点A，抛物线y＝ax2+bx+1恰好经过A，B，C三点中的两点．

（1）判断点B是否在直线y＝x+m上，并说明理由；

（2）求a，b的值；

（3）平移抛物线y＝ax2+bx+1，使其顶点仍在直线y＝x+m上，求平移后所得抛物线与y轴交点纵坐标的最大值．

9．（2021·湖北恩施土家族苗族自治州）如图，在平面直角坐标系中，四边形为正方形，点，在轴上，抛物线经过点，两点，且与直线交于另一点．

（1）求抛物线的解析式；

（2）为抛物线对称轴上一点，为平面直角坐标系中的一点，是否存在以点，，，为顶点的四边形是以为边的菱形．若存在，请求出点的坐标；若不存在，请说明理由；

（3）为轴上一点，过点作抛物线对称轴的垂线，垂足为，连接，．探究是否存在最小值．若存在，请求出这个最小值及点的坐标；若不存在，请说明理由．

10．（2020•武威）如图，在平面直角坐标系中，抛物线y＝ax2+bx﹣2交x轴于A，B两点，交y轴于点C，且OA＝2OC＝8OB．点P是第三象限内抛物线上的一动点．

（1）求此抛物线的表达式；

（2）若PC∥AB，求点P的坐标；

（3）连接AC，求△PAC面积的最大值及此时点P的坐标．

11．（2020•重庆）如图，在平面直角坐标系中，抛物线y＝ax2+bx+2（a≠0）与y轴交于点C，与x轴交于A，B两点（点A在点B的左侧），且A点坐标为（，0），直线BC的解析式为yx+2．

（1）求抛物线的解析式；

（2）过点A作AD∥BC，交抛物线于点D，点E为直线BC上方抛物线上一动点，连接CE，EB，BD，DC．求四边形BECD面积的最大值及相应点E的坐标；

（3）将抛物线y＝ax2+bx+2（a≠0）向左平移个单位，已知点M为抛物线y＝ax2+bx+2（a≠0）的对称轴上一动点，点N为平移后的抛物线上一动点．在（2）中，当四边形BECD的面积最大时，是否存在以A，E，M，N为顶点的四边形为平行四边形？若存在，直接写出点N的坐标；若不存在，请说明理由．