新课标2022版高考数学总复习第二章函数第五节指数与指数函数课件文

这是一份新课标2022版高考数学总复习第二章函数第五节指数与指数函数课件文，共41页。

学习要求:1.了解指数函数模型的实际背景.2.理解有理指数幂的含义,了解实数指数幂的意义,掌握幂的运算.3.理解指数函数的概念,理解指数函数的单调性,掌握指数函数图象通过的特 殊点.4.知道指数函数是一类重要的函数模型.
1.指数幂的概念(1)根式的概念:
　　(2)两个重要公式: = ( )n=⑨　    a　    (注意:a必须使 有意义).
2.有理数指数幂(1)分数指数幂的表示:(i)正数的正分数指数幂: =⑩　     　    (a>0,m,n∈N*,n>1).(ii)正数的负分数指数幂: = 　     　    = (a>0,m,n∈N*,n>1).(iii)0的正分数指数幂是 　　0　    ,0的负分数指数幂无意义.
(2)有理数指数幂的运算性质:(i)aras= 　    ar+s　    (a>0,r,s∈Q).(ii)(ar)s= 　    ars　    (a>0,r,s∈Q).(iii)(ab)r= 　    arbr　    (a>0,b>0,r∈Q).
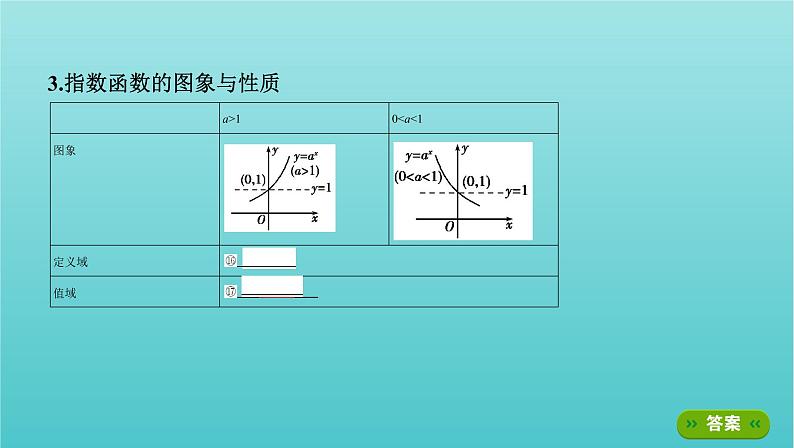
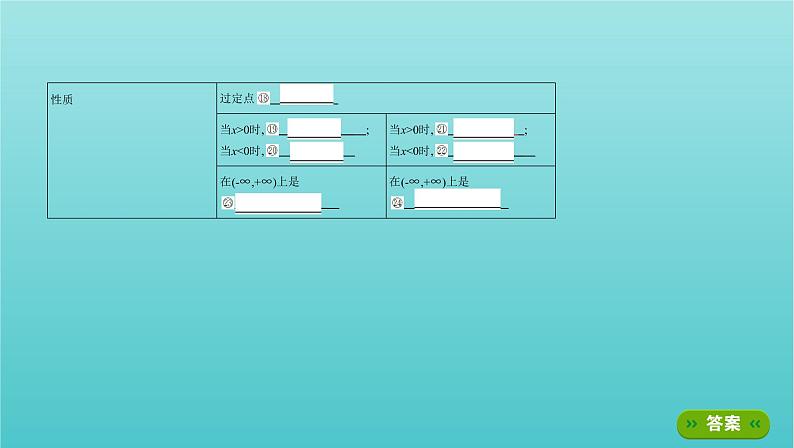
3.指数函数的图象与性质
知识拓展　　指数函数的图象与底数大小的关系.下图是指数函数(1)y=ax,(2)y=bx,(3)y =cx,(4)y=dx的图象,底数a,b,c,d与1之间的大小关系为c>d>1>a>b>0.由此我们 可以得到以下规律:在第一象限内,指数函数y=ax(a>0,且a≠1)的图象越高,底 数越大. 
1.判断正误(正确的打“√”,错误的打“✕”).(1) 与( )n都等于a(n∈N*). (　　)(2)函数y=23x与y=2x+1都不是指数函数. (　　)(3)若am0,且a≠1),则m2.函数f(x)=ax-2+1(a>0,且a≠1)的图象必经过点 (　　)A.(0,1)　　　    B.(1,1)C.(2,0)　　　    D.(2,2)
3.某种产品的产量原来是a件,在今后m年内,计划使每年的产量比上一年增加 p%,则该产品的产量y随年数x变化的函数解析式为 (　　)A.y=a(1+p%)x(04. , , 三个数从小到大的排列顺序是     < <     .
5.(2020湖南衡阳八中期中)已知指数函数f(x)=(a-1)x,若当x>0时, f(x)<1恒成立, 则实数a的取值范围是　(1,2)    .
6.(易错题)函数y= 的最小值为         .
易错分析    对复合函数的单调性理解不透彻.
角度一　根式与指数幂典例1　(1)  (a>0)的值是 (     　)A.1　　　    B.a　　　    C. 　　　    D. (2) + + + =     -1    .
典例2　化简下列各式:(1) +2-2× -(0.01)0.5;(2)  b-2·(-3 b-1)÷(4 b-3 .
解析　(1)原式=1+ × - =1+ × - =1+ - = .(2)原式=-  b-3÷(4 ·b-3 =-  b-3÷(  )=-   =- · =- .
规律总结指数幂运算的一般原则(1)有括号的先算括号里的,无括号的先进行指数运算.(2)先乘除后加减,负指数幂化成正指数幂的倒数.(3)底数是负数的,先确定符号;底数是小数的,先化成分数;底数是带分数的,先 化成假分数.(4)若是根式,则化为分数指数幂,尽可能用幂的形式表示,运用指数幂的运算 性质来解答.▶提醒    运算结果不能同时含有根号和分数指数幂,也不能既有分母又有负指数,形式力求统一.
1. =         .
2. × + × - =　2    .
考点二　指数函数的图象及应用
典例3　(1)函数f(x)=-3|x|+1的大致图象是 (     　) (2)若曲线|y|=2x+1与直线y=b没有公共点,则b的取值范围是　[-1,1]    .
◆变式探究　本例(2)中若曲线y=|2x-1|与直线y=b有两个公共点,求b的取值范 围.
方法技巧应用指数函数图象的4个技巧(1)画指数函数y=ax(a>0,a≠1)的图象,应抓住三个关键点:(1,a),(0,1), .(2)已知函数解析式判断其图象一般是取特殊点,判断所给的图象是否过这些 点,若不满足,则排除.(3)对于有关指数型函数的图象问题,一般是从最基本的指数函数的图象入 手,通过平移、伸缩、对称变换得到.特别地,当底数a与1的大小关系不确定 时,应注意分类讨论.(4)有关指数方程、不等式问题往往利用相应的指数型函数图象,数形结合求解.
1.函数y=ax- (a>0,且a≠1)的图象可能是 (　　) 
解析　∵a>0,∴ >0,∴函数y=ax需向下平移 个单位长度,不过(0,1)点,所以排除A,当a>1时,0< <1,所以排除B,当01,所以排除C,故选D.
2.已知函数f(x)=ax-2+7(a>0且a≠1)的图象恒过定点P,若定点P在幂函数g(x)的 图象上,则幂函数g(x)的图象是 (　　) 
解析　由题意知f(2)=a2-2+7=8,所以定点P的坐标为(2,8),设幂函数g(x)=xα,将P(2,8)代入得2α=8,故α=3,即g(x)=x3,故选D.
3.若关于x的方程|ax-1|=2a(a>0,a≠1)有两个不等实根,则a的取值范围是          .
解析　方程|ax-1|=2a(a>0,a≠1)有两个不等实根等价于函数y=|ax-1|的图象与y =2a的图象有两个交点.当01时,如图②,而y=2a>1,不符合题意. 所以0考点三　指数函数的性质及应用
角度一　比较指数幂的大小
典例4　(1)已知a= ,b= ,c= ,则下列关系式中正确的是 (     　)A.c角度二　解简单指数型不等式
典例5　(1)已知函数f(x)= ,则不等式f(a2-4)>f(3a)的解集为 (    )A.(-4,1)　　　    B.(-1,4)　　　    C.(1,4)　　　    D.(0,4)(2)已知 >91-x,则x的取值范围是　(-∞,-3)    .(3)已知4x-2x+1-8<0,则x的取值范围是　(-∞,2)    .
角度三　指数函数性质的综合应用
典例6　(1)函数f(x)= (e为自然对数的底数)的值域为 (     　)A.(-1,1)　　　    B.(-1,+∞)C.(-∞,1)　　　    D.(-1,0)∪(0,1)(2)若函数y= 的定义域为A,则函数y=4x-2x+1(x∈A)的值域为　[-1,8]    .
典例7　(1)函数f(x)= 的单调减区间为　(-∞,1]    .(2)已知奇函数f(x)=a- (a∈R,e为自然对数的底数).①判断f(x)的单调性(不用证明);②若对任意的实数x, f(x)>m2-4m+2恒成立,求实数m的取值范围.
解析　(1)令u=-x2+2x+1,∵y= 为减函数,∴函数y= 的单调减区间即函数u=-x2+2x+1的单调增区间.又u=-x2+2x+1的单调增区间为(-∞,1],∴函数f(x)的单调减区间为(-∞,1].(2)①f(x)是R上的单调递增函数.②∵f(x)为奇函数,∴f(-x)=-f(x),∴a- =-a+ ,∴2a=2,∴a=1,
∴f(x)=1- ,令t=ex+1,∵ex>0,∴t>1,又g(t)=1- 在(1,+∞)上为增函数,∴-1m2-4m+2对任意的实数x恒成立,∴m2-4m+2≤-1,即m2-4m+3≤0,∴1≤m≤3,故实数m的取值范围是[1,3].
1.利用指数函数的性质比较大小或解不等式,最重要的是“同底”原则.2.求解与指数函数有关的复合函数问题,要明确复合函数的构成,涉及值域、 单调区间、最值等问题时,要借助“同增异减”这一性质分析判断.
1.不等式 < 恒成立,则a的取值范围是　(-2,2)    .
2.求函数f(x)= 的定义域、值域及单调区间.
3.(2019黑龙江大庆四中高一月考)已知函数f(x)=ax-2(a>0,a≠1,x≥0)的图象经 过点(3,0.5).(1)求a的值;(2)求函数f(x)=ax-2(x≥0)的值域.