

专题5.1 相交线(知识讲解)-2021-2022学年七年级数学下册基础知识专项讲练(人教版)
展开专题5.1 相交线(知识讲解)
【学习目标】
1.了解两直线相交所成的角的位置和大小关系,理解邻补角和对顶角概念,掌握对顶角的性质;
2.理解垂直作为两条直线相交的特殊情形,掌握垂直的定义及性质;
3.理解点到直线的距离的概念,并会度量点到直线的距离;
4.能依据对顶角、邻补角及垂直的概念与性质,进行简单的计算.
【要点梳理】
知识点一、邻补角与对顶角
1.邻补角:如果两个角有一条公共边,并且它们的另一边互为反向延长线,那么具有这种关系的两个角叫做互为邻补角.
要点诠释:
(1)邻补角的定义既包含了位置关系,又包含了数量关系:“邻”指的是位置相邻,“补”指的是两个角的和为180°.
(2)邻补角是成对出现的,而且是“互为”邻补角.
(3)互为邻补角的两个角一定互补,但互补的两个角不一定互为邻补角.
(4)邻补角满足的条件:①有公共顶点;②有一条公共边,另一边互为反向延长线.
2. 对顶角及性质:
(1)定义:由两条直线相交构成的四个角中,有公共顶点没有公共边(相对)的两个角,互为对顶角.
(2)性质:对顶角相等.
要点诠释:
(1)由定义可知只有两条直线相交时,才能产生对顶角.
(2)对顶角满足的条件:①相等的两个角;②有公共顶点且一角的两边是另一角两边的反向延长线.
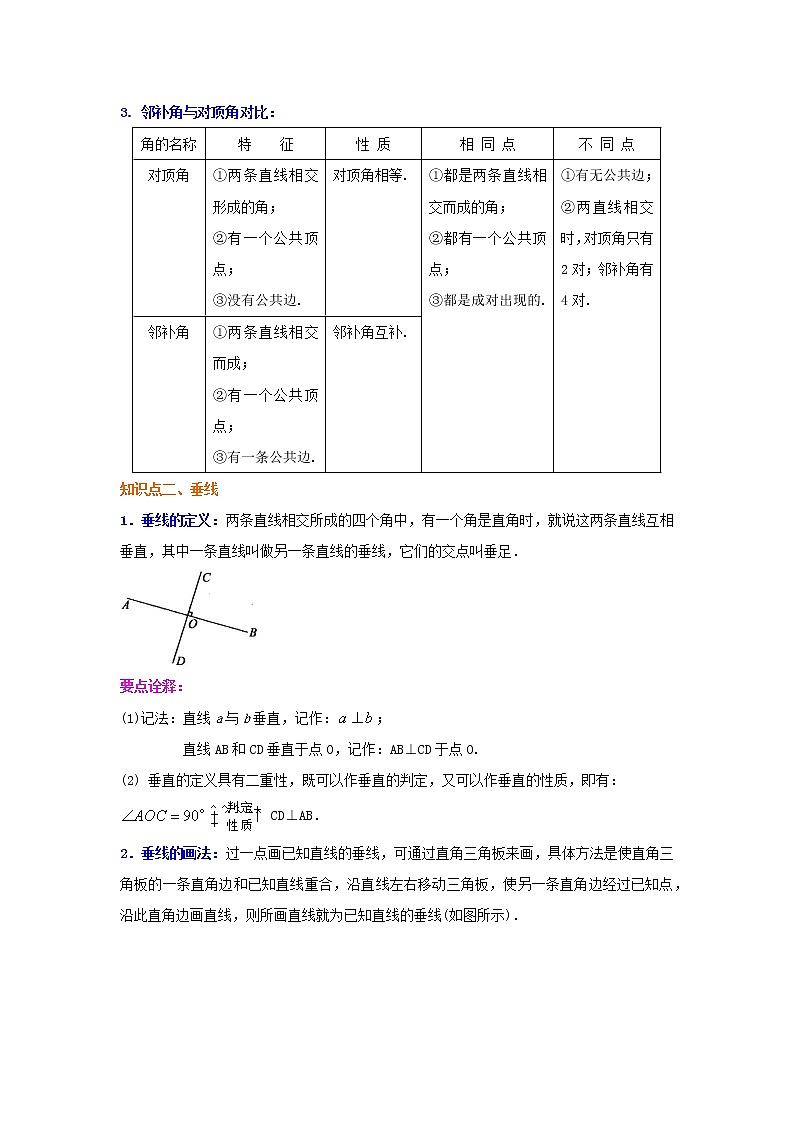
3. 邻补角与对顶角对比:
角的名称 | 特 征 | 性 质 | 相 同 点 | 不 同 点 |
对顶角 | ①两条直线相交形成的角; ②有一个公共顶点; ③没有公共边. | 对顶角相等. | ①都是两条直线相交而成的角; ②都有一个公共顶点; ③都是成对出现的. | ①有无公共边; ②两直线相交时,对顶角只有2对;邻补角有4对.
|
邻补角
| ①两条直线相交而成; ②有一个公共顶点; ③有一条公共边. | 邻补角互补. |
知识点二、垂线
1.垂线的定义:两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫垂足.
要点诠释:
(1)记法:直线a与b垂直,记作:;
直线AB和CD垂直于点O,记作:AB⊥CD于点O.
(2) 垂直的定义具有二重性,既可以作垂直的判定,又可以作垂直的性质,即有:
CD⊥AB.
2.垂线的画法:过一点画已知直线的垂线,可通过直角三角板来画,具体方法是使直角三角板的一条直角边和已知直线重合,沿直线左右移动三角板,使另一条直角边经过已知点,沿此直角边画直线,则所画直线就为已知直线的垂线(如图所示).
要点诠释:
(1)如果过一点画已知射线或线段的垂线时,指的是它所在直线的垂线,垂足可能在射线的反向延长线上,也可能在线段的延长线上.
(2)过直线外一点作已知直线的垂线,这点与垂足间的线段为垂线段.
3.垂线的性质:
(1)在同一平面内,过一点有且只有一条直线与已知直线垂直.
(2)连接直线外一点与直线上各点的所有线段中,垂线段最短.简单说成:垂线段最短.
要点诠释:
(1)性质(1)成立的前提是在“同一平面内”,“有”表示存在,“只有”表示唯一,“有且只有”说明了垂线的存在性和唯一性.
(2)性质(2)是“连接直线外一点和直线上各点的所有线段中,垂线段最短.”实际上,连接直线外一点和直线上各点的线段有无数条,但只有一条最短,即垂线段最短.在实际问题中经常应用其“最短性”解决问题.
4.点到直线的距离:
定义:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
要点诠释:
(1) 点到直线的距离是垂线段的长度,是一个数量,不能说垂线段是距离;
(2)求点到直线的距离时,要从已知条件中找出垂线段或画出垂线段,然后计算或度量垂线段的长度.
【典型例题】
类型一、邻补角与对顶角
1.如图所示,M、N是直线AB上两点,∠1=∠2,问∠1与∠2,∠3与∠4是对顶角吗? ∠1与∠5,∠3与∠6是邻补角吗?
【答案与解析】
解:∠1和∠2,∠3和∠4都不是对顶角.∠1与∠5,∠3与∠6也都不是邻补角.
【总结升华】牢记两条直线相交,才能产生对顶角或邻补角.
举一反三:
【变式】判断正误:
(1)如果两个角有公共顶点且没有公共边,那么这两个角是对顶角. ( )
(2)如果两个角相等,那么这两个角是对顶角.( )
(3)有一条公共边的两个角是邻补角. ( )
(4)如果两个角是邻补角,那么它们一定互补. ( )
(5)有一条公共边和公共顶点,且互为补角的两个角是邻补角.( )
【答案】(1)× (2)× (3)× (4)√ (5)×,反例:∠AOC为120°,射线OB为∠AOC的角平分线,∠AOB与∠AOC互补,且有边公共为AO,公共顶点为O,但它们不是邻补角.
2.如图所示,直线AB、CD相交于点O,∠1=65°,求∠2、∠3、∠4的度数
【答案与解析】
解:∵ ∠1是∠2的邻补角,∠1=65°,
∴ ∠2=180°-65°=115°.
又∵ ∠1和∠3是对顶角,∠2与∠4是对顶角
∴ ∠3=∠1=65°, ∠4=∠2=115°.
【总结升华】 (1)两条直线相交所成的四个角中,只要已知其中一个角,就可以求出另外三角;(2)求出∠2后用 “对顶角相等”,求∠3和∠4.
举一反三:
【变式】如图,已知直线AB与CD交于点O,ON平分∠DOB,若∠BOC=110°,则∠AON的度数为 度.
【答案】145.
解:∵∠BOC=110°,
∴∠BOD=70°,
∵ON为∠BOD平分线,
∴∠BON=∠DON=35°,
∵∠BOC=∠AOD=110°,
∴∠AON=∠AOD+∠DON=145°.
3. 任意画两条相交的直线,在形成的四个角中,两两相配共能组成几对角?各对角存在怎样的位置关系?根据这种位置关系将它们分类.
【答案与解析】
解:如图,
任意两条相交直线,两两相配共组成6对角,在这6对角中,它们的位置关系有两种:①有公共顶点,一边重合,另一边互为反向延长线;
②有公共顶点,角的两边互为反向延长线.
这6对角为∠1与∠2,∠1与∠3,∠1与∠4,∠2与∠3,∠2与∠4,∠3与∠4,其中∠1=∠3,∠2=∠4,∠1+∠2=180°,∠3+∠4=180°,∠1+∠4=180°,∠2+∠3=180°.在位置上∠1与∠3,∠2与∠4是对顶角,∠1与∠2,∠3与∠4,∠l与∠4,∠2与∠3是邻补角.
【总结升华】两条相交的直线,两两相配共组成6对角,这6对角中有:4对邻补角,2对对顶角
类型二、垂线
4.下列语句中,正确的有 ( )
①一条直线的垂线只有一条;
②在同一平面内,过直线上一点有且仅有一条直线与已知直线垂直;
③两直线相交,则交点叫垂足;
④互相垂直的两条直线形成的四个角一定都是直角.
A.0个 B.1个 C.2个 D.3个
【答案】C
【解析】正确的是:②④
【总结升华】充分理解垂直的定义与性质.
举一反三:
【变式1】直线外有一点P,则点P到直线的距离是( ).
A.点P到直线的垂线的长度.
B.点P到直线的垂线段.
C.点P到直线的垂线段的长度.
D.点P到直线的垂线.
【答案】C
5.如图,已知点O在直线AB上,CO⊥DO于点O,若∠1=145°,则∠3的度数为( )
A.35° B. 45° C. 55° D. 65°
【答案】C.
【解析】解:∵∠1=145°,
∴∠2=180°﹣145°=35°,
∵CO⊥DO,
∴∠COD=90°,
∴∠3=90°﹣∠2=90°﹣35°=55°.
【总结升华】本题考查了垂线和邻补角的定义;弄清两个角之间的互补和互余关系是解题的关键.
举一反三:
【变式】如图, 直线AB和CD交于O点, OD平分∠BOF, OE ⊥CD于点O, ∠AOC=40,
则∠EOF=_______.
【答案】130°.
6.如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在( )
A.A点 B.B点 C.C点 D.D点
【思路点拨】根据垂线段最短可得答案.
【答案】A.
【解析】解:根据垂线段最短可得:应建在A处,故选:A.
【总结升华】此题主要考查了垂线段的性质,关键是掌握从直线外一点到这条直线所作的垂线段最短.
举一反三:
【变式】(1)用三角尺或量角器画已知直线的垂线,这样的垂线能画出几条?
(2)经过直线上一点A画的垂线,这样的垂线能画出几条?
(3)经过直线外一点B画的垂线,这样的垂线能画出几条?
【答案】
解:(1)能画无数条;(2)能画一条;(3)能画一条.
数学七年级下册第五章 相交线与平行线5.1 相交线5.1.1 相交线同步测试题: 这是一份数学七年级下册<a href="/sx/tb_c88513_t7/?tag_id=28" target="_blank">第五章 相交线与平行线5.1 相交线5.1.1 相交线同步测试题</a>,共15页。
初中数学人教版七年级下册第五章 相交线与平行线综合与测试一课一练: 这是一份初中数学人教版七年级下册第五章 相交线与平行线综合与测试一课一练,共16页。
专题5.16 《相交线与平行线》(专项练习1)-2021-2022学年七年级数学下册基础知识专项讲练(人教版): 这是一份专题5.16 《相交线与平行线》(专项练习1)-2021-2022学年七年级数学下册基础知识专项讲练(人教版),共15页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。












