



2018年中考数学基础过关复习第三章函数第5课时二次函数的图像与性质课件新人教版_284-数学备课大师【全免费】
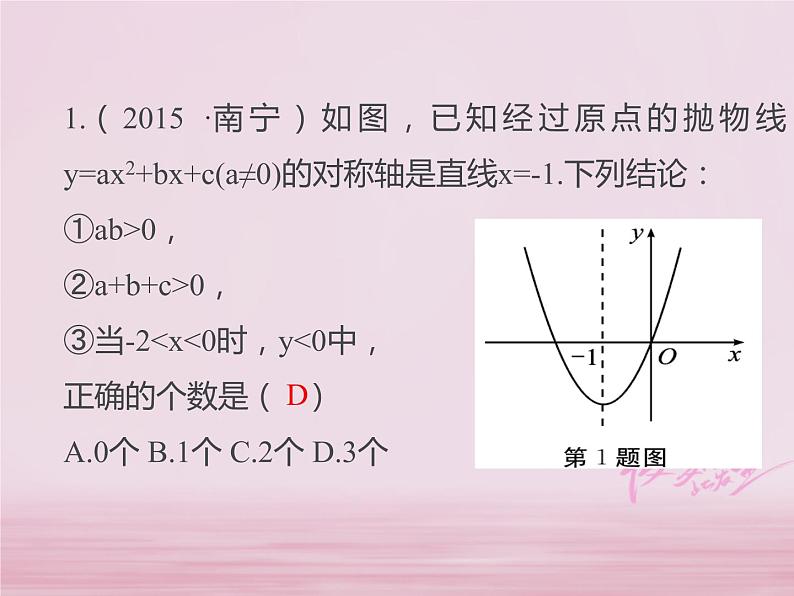
展开1.(2015 ·南宁)如图,已知经过原点的抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=-1.下列结论:①ab>0,②a+b+c>0,③当-2
焦点1 二次函数的定义1.二次函数的定义: 形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数,叫做二次函数. 特别地,当b=c=0时,y=ax2(a≠0)是二次函数的特例.
1. 自变量的最高次数是2。
2. 二次项的系数a≠0。
3. 二次函数解析式必须是整式。
思考:下列函数中,哪些是二次函数?是二次函数的,请说出它的二次项系数、一次项系数和常数项:
1,函数 (其中a、b、c为常数),当a、b、c满足什么条件时, (1)它是二次函数; (2)它是一次函数;(3)它是正比例函数;
(1)它是二次函数?(2)它是反比例函数?
2.二次函数的解析式(1)一般式:y=ax2+bx+c(a≠0);(2)顶点式:y=a(x-h)2+k(a≠0),其中(h,k)为抛物线的顶点坐标;(3)两根式(交点式):y=a(x-x1)(x-x2)(a≠0),其中x1,x2是一元二次方程a(x-x1)(x-x2)=0的两个实根.
y = ax2 + k
y = a(x – h )2
y = a( x – h )2 + k
结论: 一般地,抛物线 y = a(x-h)2+k与y = ax2形状相同,位置不同。
小结:各种形式的二次函数的关系
(1)是一条抛物线;(2)对称轴是:x=-(3)顶点坐标是:(- , )(4)开口方向: a>0时,开口向上; a<0时,开口向下.
考点2 二次函数的图象与性质
1、一般二次函数y=ax2+bx+c(a≠0)的图象特点和函数性质
(1) a>0时,对称轴左侧(x<- ),函数值y随x的增大而减小 ;对称轴右侧(x>- ),函数值y随x的增大而增大 。 a<0时,对称轴左侧(x<- ),函数值y随x的增大而增大 ;对称轴右侧(x>- ),函数值y随x的增大而减小 。 (2) a>0时,ymin= a<0时,ymax=
二次函数y=a(x-h)2+k的图象和性质
y=a(x-h)2+k(a>0)
y=a(x-h)2+k(a<0)
当x=h时,最小值为k.
当x=h时,最大值为k.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
1.a管开口方向和开口大小 (1)a管开口方向:
(2)a管抛物线的形状: ①两条抛物线的形状相同 |a1|=|a2|. ②|a|管开口大小:
2.c管在y轴上的交点(0,c)
3.b与a合作管对称轴(左同右异)
特别地,当对称轴为y轴时,b=0.
1.一般式:y=ax2+bx+c(a≠0)若已知条件是图象上三个点的坐标,则设一般式y=ax2+bx+c(a≠0),将已知条件代入,求出a,b,c的值.
y=a(x-h)2+k的图象是将图象y=ax2平移而得到的.
[温馨提示]以二次函数y=a(x-h)2+k(a≠0,a、k、h为常数)为例,函数图象的顶点坐标为B(h,k),若抛物线y=ax2的顶点坐标为A(0,0),点A到点B的平移方式也就是函数y=ax2的图象平移到函数y=a(x-h)2+k(a≠0,a、k、h为常数)的图象位置的平移方式.口诀:左加右减,上加下减.
样题1 二次函数y=ax2+bx+c的图象如图所示,则下列结论不正确的是( )A.a<0B.c>0C.a+b+c>0D.b2-4ac>0
[解析]根据抛物线的开口方向,可判断a的正负;根据抛物线与y轴的交点的位置,可判断c的正负;根据x=1时的函数值,可判断a+b+c的正负;根据抛物线与x轴有两个交点,可判断b2-4ac的符号.∵抛物线的开口向下,∴a<0.∵抛物线与y轴的交点在y轴的正半轴上,∴c>0.当x=1时,y=a+b+c<0.∵抛物线与x轴有两个交点,∴b2-4ac>0.故选择C.
1.(2016·来宾)已知函数y=-x2-2x,当 时,函数值y随x的增大而增大.2.(2017·北部湾模拟)下列关于抛物线y=-x2+2的说法正确的是 ( )A.抛物线开口向上 B.顶点坐标为(-1,2)C.在对称轴的右侧,y随x的增大而增大D.抛物线与x轴有两个交点
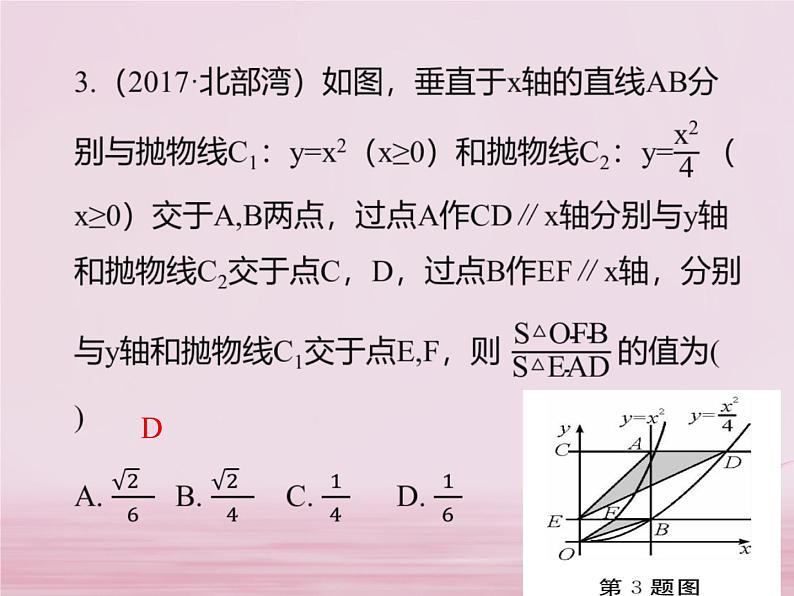
3.(2016·梧州)如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-2,0)、B(1,0),直线x=-0.5与此抛物线交于点C,与x轴交于点M,在直线上取点D,使MD=MC.连接AC、BC、AD、BD.某同学根据图象写出下列结论:①a-b=0;②当-2<x<1时,y>0;③四边形ACBD是菱形;④9a-3b+c>0.你认为其中正确的是( )A.②③④ B.①②④C.①③④ D.①②③
样题2.已知二次函数y=ax2+bx+c(a≠0)中自变量x和函数值y的部分对应值如下表:则该二次函数的解析式为 .
y=2(x-3)(x+1)
y=-2(x-1)2-6
6.(2016·5来宾)设抛物线C1:y=x2向右平移2个单位长度,再向下平移3个单位长度得到抛物线C2,则抛物线C2对应的函数解析式是( )A.y=(x-2)2-3B.y=(x+2)2-3C.y=(x-2)2+3D.y=(x+2)2+3
[分析](1)把点G坐标代入抛物线解析式求出m的值即可.(2)①对于抛物线解析式,令y=0求a出x的值,确定出点A与B坐标;令x=0,求出y的值,确定出点C坐标,求出三角形ABC面积即可.②如图1,连接BC交对称轴于点H,由对称轴的性质和两点之间线段最短可知:此时AH+CH=BH+CH=BC最小,利用待定系数法求出直线BC解析式,与抛物线对称轴联立求出点H的坐标即可.
(3)在第四象限内,抛物线上存在点M,使得以点A、B、M为顶点的三角形与△ACB相似,分两种情况考虑:△ACB∽△ABM与△ACB∽△MBA,利用相似三角形的判定与性质,确定出m的值即可.
(3)假设在第四象限内,抛物线上存在点M,使得以点A、B、M为顶点的三角形与△ACB相似,如图2,过M作MN⊥x轴,交x轴于点N.分两种情况考虑:
7.(2017·南宁江南区模拟)如图,抛物线y=-0.5x2+bx+3,与x轴交于点B(-2,0)和C,与y轴交于点A,点M在y轴上.(1)求抛物线的解析式;(2)连接BM并延长,交抛物线于D,过点D作DE⊥x轴于E.当以B,D,E为顶点的三角形与△AOC相似时,求点M的坐标;(3)连接BM,当∠OMB+∠OAB=∠ACO时,求AM的长.
解:(1)将点B(-2,0)代入y=-0.5x3+bx+3,得-0.5×(-2)2-2b+3=0,∴b=0.5,∴抛物线的解析式为y=-0.5x2+0.5x+3.
8.(2017·北部湾模拟)如图,已知抛物线y=-x2+2x+3与坐标轴交于A,B,C三点,抛物线上的点D与点C关于它的对称轴对称.(1)直接写出点D的坐标和直线AD的解析式;(2)点E是抛物线上位于直线AD上方的动点,过点E分别作EF∥x轴,EG∥y轴并交直线AD于点F,G,求△EFG周长的最大值;
(3)若点P为y轴上的动点,则在抛物线上是否存在点Q,使得以A,D,P,Q为顶点的四边形是平行四边形?若存在,请求出点Q的坐标,若不存在,请说明理由.
(3)存在.①以AD为平行四边形的边时,PQ∥AD,PQ=AD.∵A,D两点间的水平距离为3,∴P,Q两点间的水平距离也为3.∴点Q的横坐标为3或-3.将x=3和x=-3分别代入y=-x2+2x+3,得y=0或y=-12.∴Q(3,0)或Q(-3,-12).
②当AD为平行四边形的对角线时,PD∥AQ,PD=AQ,可以看作PD平称得到AQ.又∵A(-1,0),D(2,3),∴点Q的横坐标为1.将x=1代入y=-x2+2x+3,得y=4.∴点Q的坐标为(1,4).综上所述,当点Q的坐标为(3,0)或(-3,-12)或(1,4)时,以A,D,P,Q为顶点的四边形是平行四边形.
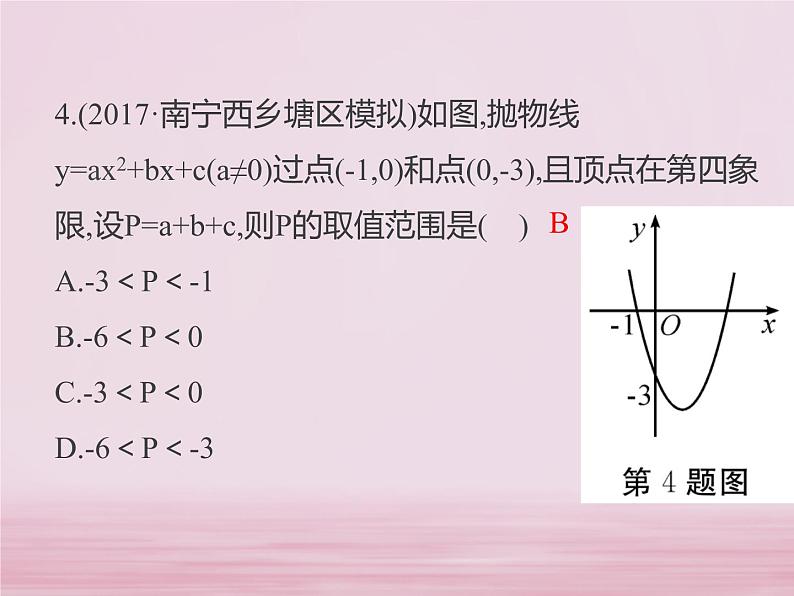
1、填空:(1)二次函数y=x2-x-6的图象顶点坐标是___________对称轴是_________。(2)抛物线y=-2x2+4x与x轴的交点坐标是___________(3)已知函数y=—x2-x-4,当函数值y随x的增大而减小时,x的取值范围是___________(4)二次函数y=mx2-3x+2m-m2的图象经过原点,则m= ____。
2.选择抛物线y=x2-4x+3的对称轴是_____________. A 直线x=1 B直线x= -1 C 直线x=2 D直线x= -2(2)抛物线y=3x2-1的________________ A 开口向上,有最高点 B 开口向上,有最低点 C 开口向下,有最高点 D 开口向下,有最低点(3)若y=ax2+bx+c(a 0)与轴交于点A(2,0), B(4,0), 则对称轴是_______ A 直线x=2 B直线x=4 C 直线x=3 D直线x= -3
(4)若y=ax2+bx+c(a 0)与轴交于点A(2,m), B(4,m), 则对称轴是_______ A 直线x=3 B 直线x=4 C 直线x= -3 D直线x=2
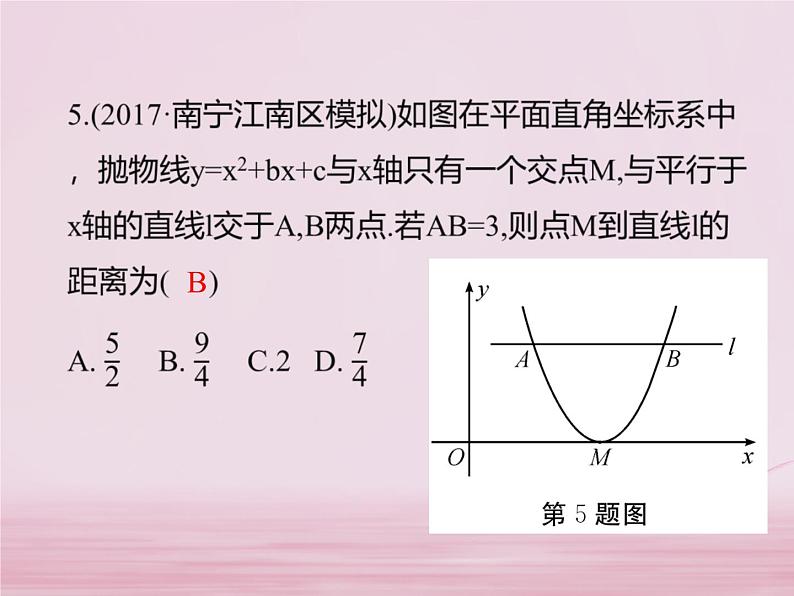
3、解答题:已知二次函数的图象的顶点坐标为(-2,-3),且图象过点(-3,-2)。 (1)求此二次函数的解析式; (2)设此二次函数的图象与x轴交于A,B两点,O为坐标原点,求线段OA,OB的长度之和。
1、 二次函数的图象如图所示,则在下列各不等式中成立的个数是____________
①abc<0 ②a+b+c < 0 ③a+c > b④2a+b=0 ⑤Δ=b-4ac > 0
2、已知二次函数y=ax2-5x+c的图象如图。
(1)、当x为何值时,y随x的增大而增大;
(2)、当x为何值时,y<0。
(3)、求它的解析式和顶点坐标;
2018年中考数学基础过关复习第三章函数第6课时二次函数的应用课件新人教版_285-数学备课大师【全免费】: 这是一份2018年中考数学基础过关复习第三章函数第6课时二次函数的应用课件新人教版_285-数学备课大师【全免费】,共51页。PPT课件主要包含了中考考什么,核心考点解读,b2–4ac,怎么考,补充练习等内容,欢迎下载使用。
2018年中考数学基础过关复习第三章函数第4课时一次函数与反比例函数的综合课件新人教版_283-数学备课大师【全免费】: 这是一份2018年中考数学基础过关复习第三章函数第4课时一次函数与反比例函数的综合课件新人教版_283-数学备课大师【全免费】,共22页。PPT课件主要包含了中考考什么,核心考点解读,怎么考,补充练习等内容,欢迎下载使用。
2018年中考数学基础过关复习第三章函数第3课时反比例函数课件新人教版_282-数学备课大师【全免费】: 这是一份2018年中考数学基础过关复习第三章函数第3课时反比例函数课件新人教版_282-数学备课大师【全免费】,共56页。PPT课件主要包含了中考考什么,核心考点解读,m2-2-1,m-1≠0,m±1,m≠1,与面积有关的问题,怎么考,补充练习等内容,欢迎下载使用。












