【历年真题】中考数学三年高频真题汇总 卷（Ⅱ）（含答案及解析）

中考数学三年高频真题汇总 卷（Ⅱ）

 考试时间：90分钟；命题人：数学教研组

考生注意：

1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟

2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上

3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题  30分）

一、单选题（10小题，每小题3分，共计30分）

1、要使式子有意义，则（　　）

A． B． C． D．

2、已知关于x的不等式组的解集是3≤x≤4，则a+b的值为（　　）

A．5 B．8 C．11 D．9

3、下列命题中，真命题是（　　）

A．同位角相等

B．有两条边对应相等的等腰三角形全等

C．互余的两个角都是锐角

D．相等的角是对顶角．

4、截至2021年12月31日，我国已有11.5亿人完成了新冠疫苗全程接种，数据11.5亿用科学记数法表示为（    ）

A．11.5×108 B．1.15×108 C．11.5×109 D．1.15×109

5、已知抛物线的对称轴为直线，与轴的一个交点坐标为，其部分图象如图所示，下列结论中：①；②；③抛物线与轴的另一个交点的坐标为；④方程有两个不相等的实数根．其中正确的个数为（    ）

A．个 B．个 C．个 D．个

6、的相反数是（    ）

A． B． C． D．3

7、下图中能体现∠1一定大于∠2的是（　　）

A． B．

C． D．

8、如图，已知AD∥BC，欲用“边角边”证明△ABC≌△CDA，需补充条件（　　）

A．AB = CD B．∠B = ∠D C．AD = CB D．∠BAC = ∠DCA

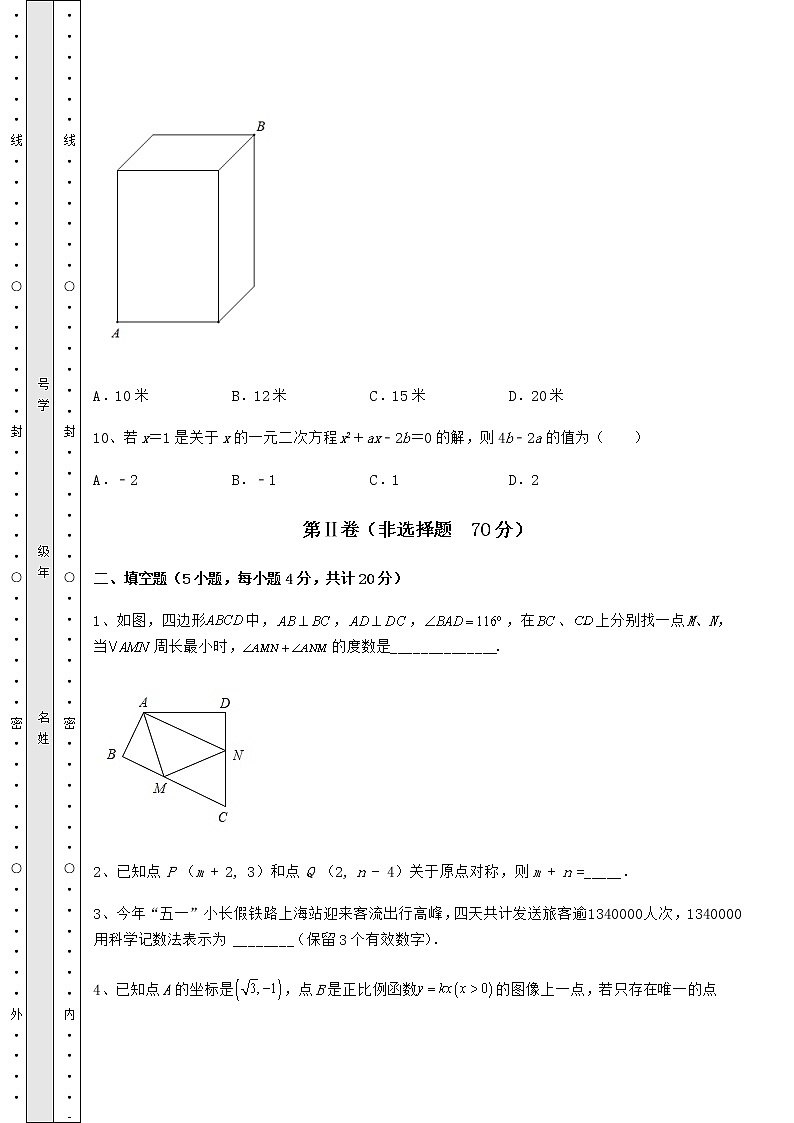
9、如图，四棱柱的高为9米，底面是边长为6米的正方形，一只蚂蚁从如图的顶点A开始，爬向顶点B．那么它爬行的最短路程为（　　）

A．10米 B．12米 C．15米 D．20米

10、若x＝1是关于x的一元二次方程x2＋ax﹣2b＝0的解，则4b﹣2a的值为（    ）

A．﹣2 B．﹣1 C．1 D．2

第Ⅱ卷（非选择题  70分）

二、填空题（5小题，每小题4分，共计20分）

1、如图，四边形中，，，，在、上分别找一点M、N，当周长最小时，的度数是______________．

2、已知点 P （m + 2, 3）和点 Q （2, n - 4）关于原点对称，则 m + n =_____．

3、今年“五一”小长假铁路上海站迎来客流出行高峰，四天共计发送旅客逾1340000人次，1340000用科学记数法表示为 ________（保留3个有效数字）．

4、已知点A的坐标是，点B是正比例函数的图像上一点，若只存在唯一的点B，使为等腰三角形，则k的取值范围是______．

5、若将数轴折叠，使得表示-1的点与表示5的点重合，则原点与表示_______的点重合．

三、解答题（5小题，每小题10分，共计50分）

1、如图，数轴上A、B、C三点所对应的数分别是a、b、c．且a、b、c满足|a＋24|＋（b＋10）2＋（c－10）2＝0．

（1）则a＝_____，b＝_____，c＝_____．

（2）有一动点P从点A出发，以每秒4个单位的速度向右运动．经过t秒后，点P到点A、B、C的距离和是多少（用含t的代数式表示）？

（3）在（2）的条件下，当点P移动到点B时立即掉头，速度不变，同时点T和点Q分别从点A和点C出发，向左运动，点T的速度1个单位/秒，点Q的速度5个单位/秒，设点P，Q，T所对应的数分别是xP，xQ，xT，点Q出发的时间为t，当＜t＜时，求的值．

2、已知：如图，Rt△ABC中，∠C＝90°，CA＝CB，D是边CB上一点，DE⊥AB于点E，且CD＝BE．求证：AD平分∠BAC．

3、如图，在长方形中，，．延长到点，使，连接．动点从点出发，沿着以每秒1个单位的速度向终点运动，点运动的时间为秒．

（1）的长为          ；

（2）连接，求当为何值时，；

（3）连接，求当为何值时，是直角三角形；

（4）直接写出当为何值时，是等腰三角形．

4、如图，射线、、、分别表示从点出发的向北、东、南、西四个方向，将直角三角尺的直角顶点与点重合．

（1）图中与互余的角是_______；

（2）①用直尺和圆规作的平分线；（不写作法，保留作图痕迹）

②在①所做的图形中，如果，那么点在点的_______方向．

5、如图，已知AE平分∠BAC交BC于点E，AF平分∠CAD交BC的延长线于点F，∠B＝64°，∠EAF＝58°，试判断AD与BC是否平行．

解：∵AE平分∠BAC，AF平分∠CAD（已知），

∴∠BAC＝2∠1，∠CAD＝　　（ 　　）．

又∵∠EAF＝∠1+∠2＝58°，

∴∠BAD＝∠BAC+∠CAD

＝2（∠1+∠2）

＝　　°（等式性质）．

又∵∠B＝64°（已知），

∴∠BAD+∠B＝　　°．

∴　　　　（ 　　）．

-参考答案-

一、单选题

1、B

【分析】

根据分式有意义的条件，分母不为0，即可求得答案．

【详解】

解：要使式子有意义，

则

故选B

【点睛】

本题考查了分式有意义的条件，理解分式有意义的条件是“分母不为0”是解题的关键．

2、C

【分析】

分别求出每一个不等式的解集，结合不等式组的解集求出a、b的值，代入计算即可．

【详解】

解：解不等式x-a≥1，得：x≥a+1，

解不等式x+5≤b，得：x≤b-5，

∵不等式组的解集为3≤x≤4，

∴a+1=3，b-5=4，

∴a=2，b=9，

则a+b=2+9=11，

故选：C．

【点睛】

本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．

3、C

【分析】

根据平行线的性质、全等三角形的判定定理、余角的概念、对顶角的概念判断即可．

【详解】

解：A、两直线平行，同位角相等，故本选项说法是假命题；

B、有两条边对应相等的等腰三角不一定形全等，故本选项说法是假命题；

C、互余的两个角都是锐角，本选项说法是真命题；

D、相等的角不一定是对顶角，例如，两直线平行，同位角相等，此时两个同位角不是对顶角，故本选项说法是假命题；

故选：C．

【点睛】

本题考查的是命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．

4、D

【分析】

科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正数；当原数的绝对值＜1时，n是负数．

【详解】

解：11.5亿＝1150000000＝1.5×109．

故选：D．

【点睛】

此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．

5、C

【分析】

根据对称轴及抛物线与轴交点情况进行推理，进而对所得结论进行判断．

【详解】

解：①如图，开口向上，得，

，得，

抛物线与轴交于负半轴，即，

，

故①错误；

②如图，抛物线与轴有两个交点，则；

故②正确；

③由对称轴是直线，抛物线与轴的一个交点坐标为，得到：抛物线与轴的另一个交点坐标为，

故③正确；

④如图所示，当时，，

根的个数为与图象的交点个数，

有两个交点，即有两个根，

故④正确；

综上所述，正确的结论有3个．

故选：C．

【点睛】

主要考查抛物线与轴的交点，二次函数图象与二次函数系数之间的关系，解题的关键是会利用对称轴的范围求与的关系，以及二次函数与方程之间的转换，根的判别式的熟练运用．

6、D

【分析】

根据只有符号不同的两个数是互为相反数解答即可．

【详解】

解：的相反数是3，

故选D．

【点睛】

本题考查了相反数的定义，只有符号不同的两个数是互为相反数，正数的相反数是负数，0的相反数是0，负数的相反数是正数．

7、C

【分析】

由对顶角的性质可判断A，由平行线的性质可判断B，由三角形的外角的性质可判断C，由直角三角形中同角的余角相等可判断D，从而可得答案.

【详解】

解：A、∠1和∠2是对顶角，∠1＝∠2．故此选项不符合题意；

B、如图，

若两线平行，则∠3＝∠2，则

若两线不平行，则大小关系不确定，所以∠1不一定大于∠2．故此选项不符合题意；

C、∠1是三角形的外角，所以∠1＞∠2，故此选项符合题意；

D、根据同角的余角相等，可得∠1＝∠2，故此选项不符合题意．

故选：C．

【点睛】

本题考查的是对顶角的性质，平行线的性质，直角三角形中两锐角互余，三角形的外角的性质，同角的余角相等，掌握几何基本图形，基本图形的性质是解本题的关键.

8、C

【分析】

由平行线的性质可知，再由AC为公共边，即要想利用“边角边”证明△ABC≌△CDA，可添加AD=CB即可．

【详解】

∵AD∥BC，

∴．

∵AC为公共边，

∴只需AD=CB，即可利用“边角边”证明△ABC≌△CDA．

故选：C．

【点睛】

本题考查平行线的性质，三角形全等的判定．理解“边角边”即为两边及其夹角是解答本题的关键．

9、C

【分析】

将立体图形展开，有两种不同的展法，连接AB，利用勾股定理求出AB的长，找出最短的即可．

【详解】

解：如图，

（1）AB＝＝；

（2）AB＝＝15，

由于15＜，

则蚂蚁爬行的最短路程为15米．

故选：C．

【点睛】

本题考查了平面展开--最短路径问题，要注意，展开时要根据实际情况将图形安不同形式展开，再计算．

10、D

【分析】

将x=1代入原方程即可求出答案．

【详解】

解：将x=1代入原方程可得：1+a-2b=0，

∴a-2b=-1，

∴原式=-2（a-2b）

=2，

故选：D．

【点睛】

本题考查一元二次方程，解题的关键是正确理解一元二次方程的解的概念，本题属于基础题型．

二、填空题

1、128°

【分析】

分别作点A关于BC、DC的对称点E、F，连接EF、DF、BE ，则当M、N在线段EF上时△AMN的周长最小，此时由对称的性质及三角形内角和定理、三角形外角的性质即可求得结果．

【详解】

分别作点A关于BC、DC的对称点E、F，连接EF、DF、BE，如图

由对称的性质得：AN=FN，AM=EM

∴∠F=∠NAD，∠E=∠MAB

∵AM+AN+MN=EM+FN+MN≥EF

∴当M、N在线段EF上时，△AMN的周长最小

∵∠AMN+∠ANM=∠E+∠MAB+∠F+∠NAD=2∠E+2∠F=2(∠E+∠F)=2(180°−∠BAD)=2×(180°−116°)=128°

故答案为：128°

【点睛】

本题考查了对称的性质，两点间线段最短，三角形内角和定理与三角形外角的性质等知识，作点A关于BC、DC的对称点是本题的关键．

2、-3

【分析】

求解的值，然后代入求解即可．

【详解】

解：由题意知

解得

∴

故答案为：．

【点睛】

本题考查了关于原点对称的点坐标的特征．解题的关键在于明确关于原点对称的点坐标的横、纵坐标均互为相反数．

3、1.34×106

【分析】

科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正数；当原数的绝对值＜1时，n是负数．

【详解】

解：1340000人次，用科学记数法表示为 1.34×106人次，

故答案为：1.34×106．

【点睛】

此题考查科学记数法，注意n的值的确定方法，当原数大于10时，n等于原数的整数数位减1，按此方法即可正确求解．

4、

【分析】

作OA的垂直平分线，交OA于点C，y轴于点D．根据题意结合垂直平分线的性质可判断出当该正比例函数图象在与OA的垂直平分线平行的直线（包括此直线）和y轴之间时，在x>0的条件下，该函数图象上只存在唯一的点B，使为等腰三角形．再根据点A的坐标，即可求出直线CD的斜率，即可得出k的取值范围．

【详解】

如图，作OA的垂直平分线，交OA于点C，y轴于点D．

由垂直平分线的性质可知，当点B在OA的垂直平分线上时，即满足为等腰三角形，但此时在该正比例函数上还有一点B可使为等腰三角形，如图，和都为等腰三角形，此时不符合只存在唯一的点B，使为等腰三角形，

故要想只存在唯一的点B，使为等腰三角形，并在x>0的条件下，只能B点不在OA的垂直平分线上，即该正比例函数图象在与OA的垂直平分线平行的直线（包括此直线）和y轴之间．

设OA的函数解析式为：，则

解得：．

设CD的函数解析式为：，

∵CD在OA的垂直平分线上，

∴，即，

解得：．

∵该正比例函数图象在与OA的垂直平分线平行的直线（包括此直线）和y轴之间，

∴，即．

故答案为：．

【点睛】

本题考查垂直平分线的性质，等腰三角形的定义，一次函数和正比例函数的图像和性质，根据题意理解当该正比例函数图象在与OA的垂直平分线平行的直线（包括此直线）和y轴之间时，在x>0的条件下，该函数图象上只存在唯一的点B，使为等腰三角形是解答本题的关键．

5、4

【分析】

设原点与表示x的点重合，先根据题意求出数轴上折叠的那个地方表示的数为，则，由此即可得到答案．

【详解】

解：设原点与表示x的点重合，

∵将数轴折叠，使得表示-1的点与表示5的点重合，

∴数轴上折叠的那个地方表示的数为，

∴，

解得，

故答案为：4．

【点睛】

本题主要考查了数轴上两点中点的计算方法，解一元一次方程，解题的关键在于能够根据题意求出折叠点表示的数．

三、解答题

1、（1）；（2）设经过t秒后，点P到点A、B、C的距离和为，则；（3）0

【分析】

（1）利用绝对值的非负性及完全平方的非负性求解；

（2）需要进行分类讨论，分别为当点在线段上时，当点在线段上时，当点在线段的延长线上时，进行分类讨论；

（3）先分别求出当点追上的时间，当点追上的时间，当点追上的时间，根据当时，得出三点表示的数的大小关系，即可化简求值．

【详解】

解（1），

，

，

故答案是：；

（2）设经过t秒后，点P到点A、B、C的距离和为，

①当点在线段上时，则，

点P到点A、B、C的距离和是：；

②当点在线段上时，则，

点P到点A、B、C的距离和是：；

③当点在线段的延长线上时，则

点P到点A、B、C的距离和是：；

；

（3）当点追上的时间，

当点追上的时间，

当点追上的时间，

当时，

位置如图：

，

．

【点睛】

本题考查了绝对值、数轴上的动点问题、列代数式，解题的关键是利用数形结合思想及分论讨论思想求解．

2、见解析

【分析】

先证明为等腰直角三角形，得出，再证明，得出，即可证明．

【详解】

解：，

为等腰直角三角形，

，

又，

为等腰直角三角形，

，

，

，

，

，

，

平分．

【点睛】

本题考查了等腰直角三角形、三角形全等的判定及性质、角平分线，解题的关键是掌握三角形的全等的证明．

3、（1）5；（2）秒时，；（3）当秒或秒时，是直角三角形；（4）当秒或秒或秒时，为等腰三角形．

【分析】

（1）根据长方形的性质及勾股定理直接求解即可；

（2）根据全等三角形的性质可得：，即可求出时间t；

（3）分两种情况讨论：①当时，在两个直角三角形中运用两次勾股定理，然后建立等量关系求解即可；②当时，此时点P与点C重合，得出，即可计算t的值；

（4）分三种情况讨论：①当时，②当时，③当时，分别结合图形，利用各边之间的关系及勾股定理求解即可得．

【详解】

解：（1）∵四边形ABCD为长方形，

∴，，

在中，

，

故答案为：5；

（2）如图所示：当点P到如图所示位置时，，

∵，，

∴，仅有如图所示一种情况，

此时，，

∴，

∴秒时，；

（3）①当时，如图所示：

在中，

，

在中，

，

∴，

，，

∴，

解得：；

②当时，此时点P与点C重合，

∴，

∴；

综上可得：当秒或秒时，是直角三角形；

（4）若为等腰三角形，分三种情况讨论：

①当时，如图所示：

∵，，

∴，

∴，

∴；

②当时，如图所示：

，

∴；

③当时，如图所示：

，

∴，

在中，

，

即，

解得：，

，

∴；

综上可得：当秒或秒或秒时，为等腰三角形．

【点睛】

题目主要考查勾股定理解三角形，等腰三角形的性质，全等三角形的性质等，理解题意，分类讨论作出相应图形是解题关键．

4、

（1）、

（2）①作图见解析；②北偏东或东偏北

【分析】

（1）由题可知，故可知与互余的角；

（2）①如图所示，以O为圆心画弧，分别与OE、OA相交；以两交点为圆心，大于两点长度的一半为半径画弧，连接两弧交点与O点的射线即为角平分线；②，，进而得出P与O有关的位置．

（1）

解：图中与互余的角是和；

故答案为：、．

（2）

①如图，为所作；

②，

，

平分，

，

，

即点在点的北偏东方向或东偏北

故答案为：北偏东或东偏北．

【点睛】

本题考查了余角，角平分线以及坐标系中的位置．解题的关键在于正确的求解角度．

5、2∠2；角平分线的定义；116；180；AD；BC；同旁内角互补，两直线平行

【分析】

由AE平分∠BAC，AF平分∠CAD，利用角平分线的定义可得出∠BAC＝2∠1，∠CAD＝2∠2，结合∠EAF＝∠1+∠2＝58°可得出∠BAD＝116°，由∠B＝64°，∠BAD＝116°，可得出∠BAD+∠B＝180°，再利用“同旁内角互补，两直线平行”即可得出AD∥BC．

【详解】

解：∵AE平分∠BAC，AF平分∠CAD（已知），

∴∠BAC＝2∠1，∠CAD＝2∠2（角平分线的定义）．

又∵∠EAF＝∠1+∠2＝58°，

∴∠BAD＝∠BAC+∠CAD

＝2（∠1+∠2）

＝116°（等式性质）．

又∵∠B＝64°（已知），

∴∠BAD+∠B＝180°．

∴AD∥BC（同旁内角互补，两直线平行）．

故答案为：2∠2；角平分线的定义；116；180；AD；BC；同旁内角互补，两直线平行．

【点睛】

此题考查了角平分线的定义，角的计算，平行线的判定．正确掌握线段、角、相交线与平行线的知识是解题的关键，还需掌握推理能力．