数学冀教版第二十章 函数综合与测试综合训练题

这是一份数学冀教版第二十章 函数综合与测试综合训练题，共20页。试卷主要包含了如图，点A的坐标为等内容，欢迎下载使用。
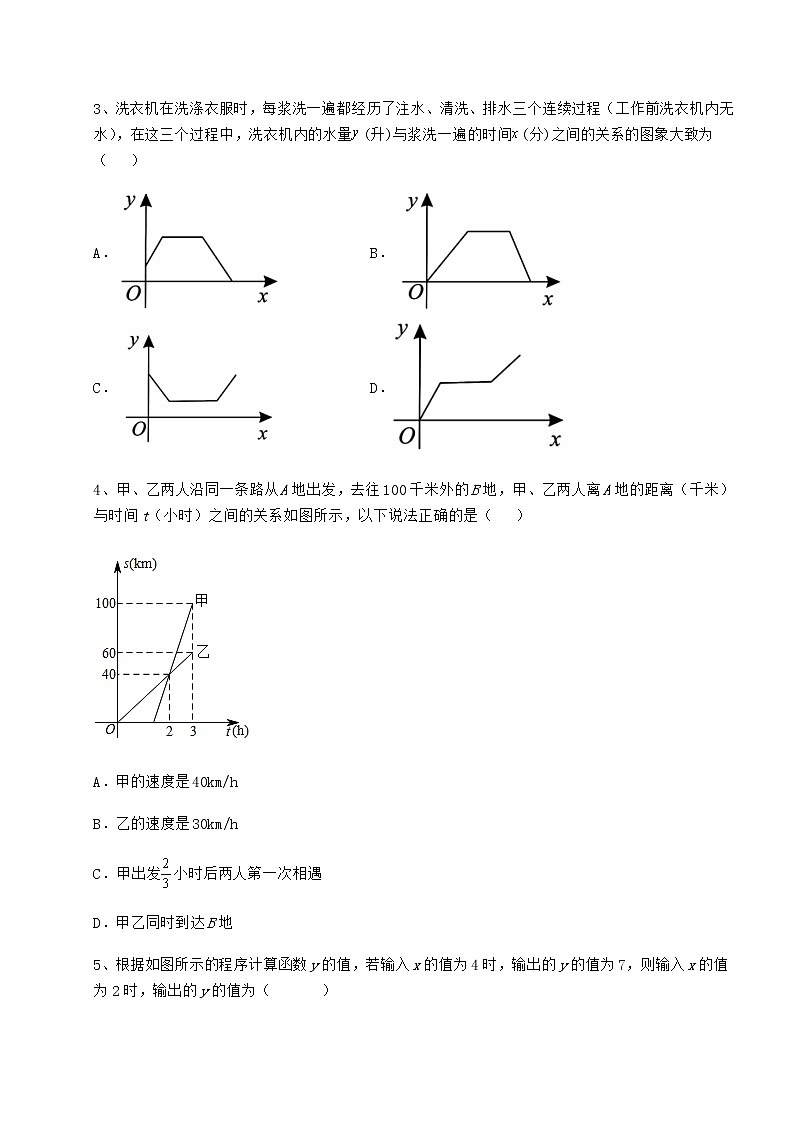
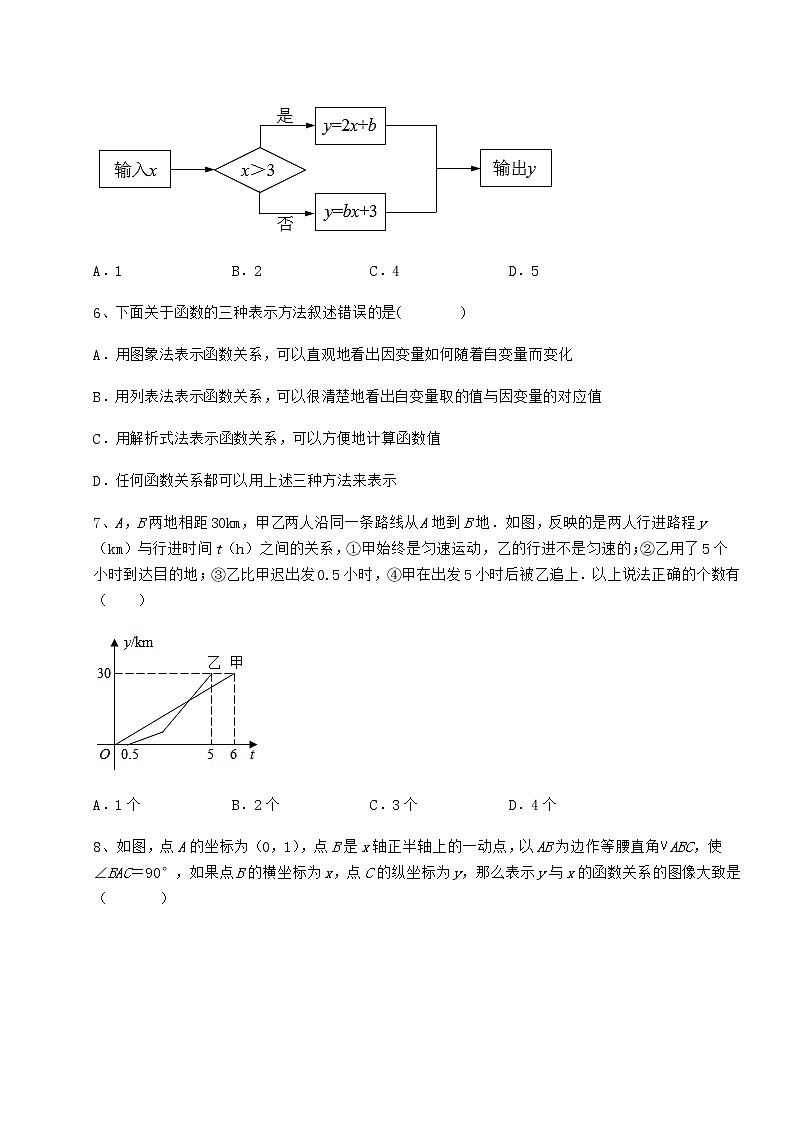
冀教版八年级数学下册第二十章函数章节训练 考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。第I卷（选择题  30分）一、单选题（10小题，每小题3分，共计30分）1、根据如图所示的程序计算函数的值，若输入的值为1，则输出的值为2；若输入的值为，则输出的值为（       ）．A． B． C．4 D．82、如图1，在矩形ABCD中，AB＜BC，AC，BD交于点O．点E为线段AC上的一个动点，连接DE，BE，过E作EF⊥BD于F．设AE＝x，图1中某条线段的长为y，若表示y与x的函数关系的图象大致如图2所示，则这条线段可能是图1中的（       ）．A．线段EF B．线段DE C．线段CE D．线段BE3、洗衣机在洗涤衣服时，每浆洗一遍都经历了注水、清洗、排水三个连续过程（工作前洗衣机内无水），在这三个过程中，洗衣机内的水量(升)与浆洗一遍的时间(分)之间的关系的图象大致为（   ）A． B．C． D．4、甲、乙两人沿同一条路从A地出发，去往100千米外的B地，甲、乙两人离A地的距离（千米）与时间t（小时）之间的关系如图所示，以下说法正确的是（　　）A．甲的速度是40km/hB．乙的速度是30km/hC．甲出发小时后两人第一次相遇D．甲乙同时到达B地5、根据如图所示的程序计算函数y的值，若输入x的值为4时，输出的y的值为7，则输入x的值为2时，输出的y的值为（       ）A．1 B．2 C．4 D．56、下面关于函数的三种表示方法叙述错误的是(        )A．用图象法表示函数关系，可以直观地看出因变量如何随着自变量而变化B．用列表法表示函数关系，可以很清楚地看出自变量取的值与因变量的对应值C．用解析式法表示函数关系，可以方便地计算函数值D．任何函数关系都可以用上述三种方法来表示7、A，B两地相距30km，甲乙两人沿同一条路线从A地到B地．如图，反映的是两人行进路程y（km）与行进时间t（h）之间的关系，①甲始终是匀速运动，乙的行进不是匀速的；②乙用了5个小时到达目的地；③乙比甲迟出发0.5小时，④甲在出发5小时后被乙追上．以上说法正确的个数有（　　）A．1个 B．2个 C．3个 D．4个8、如图，点A的坐标为（0，1），点B是x轴正半轴上的一动点，以AB为边作等腰直角ABC，使∠BAC＝90°，如果点B的横坐标为x，点C的纵坐标为y，那么表示y与x的函数关系的图像大致是（       ）A． B．C． D．9、甲、乙两人分别从A、B两地同时出发，相向而行，匀速前往B地、A地，两人相遇时停留了4min，又各自按原速前往目的地，到达目的地后停止. 甲、乙两人之间的距离y（m）与甲所用时间x（min）之间的函数关系如图所示，给出下列结论：①A，B之间的距离为1200m；②乙行走的速度是甲的1.5倍；③b＝800；④a＝34，其中正确的结论个数为（　　）A．4个 B．3个 C．2个 D．1个10、变量x与y之间的关系是，当时，自变量x的值是（       ）A．13 B．5 C．2 D．3第Ⅱ卷（非选择题  70分）二、填空题（5小题，每小题4分，共计20分）1、小明使用图形计算器探究函数的图象，他输入了一组，的值，得到了如图的函数图象，由学习函数的经验，可以推断出小明输入的__0，__0．（填“”，“”或“” 2、如图是汽车加油站在加油过程中，加油器仪表某一瞬间的显示，加油过程中的常量是________．3、如图①，在直角梯形ABCD中，动点P从点B出发，沿BC、CD运动至点D停止，设点P运动的路程为x，△ABP的面积为y．若y关于x的函数图象如图②所示，则△BCD的面积是______．4、一般地，对于一个函数，如果把自变量与函数的每对对应值分别作为点的横、纵坐标，那么坐标平面内由这些点组成的图形，就是这个函数的______．5、汽车以60km/h的速度匀速行驶，行驶路程为 s km，行驶时间为 t h，如表：t/h12345s/km60120180240300可知：路程 ＝____________（1）在上面这个过程中，变化的量是_______、_________．不变化的量是_____________．（2）试用含t的式子表示s：s＝_______．这个问题反映了匀速行驶的汽车所行驶的路程____随行驶时间___的变化过程．三、解答题（5小题，每小题10分，共计50分）1、如图所示，小明家、食堂、图书馆在同一条直线上．小明从家去食堂吃早餐，接着去图书馆读报，然后回家．如图反映了这个过程中，小明离家的距离y与时间x之间的对应关系． 根据图象回答下列问题：（1）食堂离小明家多远？小明从家到食堂用了多少时间？（2）小明吃早餐用了多少时间？（3）食堂离图书馆多远？小明从食堂到图书馆用了多少时间？（4）小明读报用了多少时间？（5）图书馆离小明家多远？小明从图书馆回家的平均速度是多少？2、如图是某一天北京与上海的气温随时间变化的图象．（1）这一天内，上海与北京何时气温相同？（2）这一天内，上海在哪段时间比北京气温高？在哪段时间比北京气温低？3、已知某函数图象如图所示，请回答下列问题：(1)自变量的取值范围是         (2)函数值的取值范围是         (3)当为     时，函数值最大；当为     时，函数值最小(4)当随的增大而增大时，的取值范围是            4、如果用c表示摄氏温度（），f表示华氏温度（），则c和f之间的关系是：．某日伦敦和纽约的最高气温分别为和，请把它们换算成摄氏温度．5、下表是小华做观察水的沸腾实验时所记录的数据：时间（分）0123456789101112温度（℃）6065707580859095100100100100100（1）时间是8分钟时，水的温度为_____；（2）此表反映了变量_____和_____之间的关系，其中_____是自变量，_____是因变量； -参考答案-一、单选题1、A【解析】【分析】输入，则有；输入，则有，将代数式的值代入求解即可．【详解】解：输入，则有；输入，则有；故选A．【点睛】本题考查了程序流程图与代数式求值．解题的关键在于正确求解代数式的值．2、B【解析】【分析】根据各个选项中假设的线段，可以分别由图象得到相应的y随x的变化的趋势，从而可以判断哪个选项是正确的．【详解】解：A、由图1可知，若线段EF是y，则y随x的增大先减小后增大，而由大变小的距离等于由小变大的距离，故此选项不符合题意；B、由图1可知，若线段DE是y，则y随x的增大先减小再增大，而由大变小的距离大于由小变大的距离，在点A的距离是DA，在点C时的距离是DC，DA＞DC，故此选项符合题意；C、由图1可知，若线段CE是y，则y随x的增大越来越小，故此选项不符合题意；D、由图1可知，若线段BE是y，则y随x的增大先减小再增大，而由由大变小的距离小于由小变大的距离，在点A的距离是BA，在点C时的距离是BC，BA＜BC，故此选项不符合题意；故选B．【点睛】本题考查动点问题的函数图象，解题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答问题．3、B【解析】【分析】根据洗衣机内水量开始为0，注水后水量变多，清洗时水量不变，排水时水量变小，直到水量变为0；由此即可得到答案．【详解】解：解：因为洗衣机工作前洗衣机内无水，所以A，C两选项不正确，被淘汰；又因为洗衣机最后排完水，所以D选项不正确，被淘汰，所以选项B正确．故选：B．【点睛】本题考查了对函数图象的理解能力．解题关键是看函数图象要理解两个变量的变化情况．4、C【解析】【分析】根据题意和函数图象中的数据，可以判断各个小题中的结论是否正确，从而可以解答本题．【详解】解：由图可得， 甲车出发第小时时距离A地千米，甲车出发第小时时距离A地千米，甲车的速度是千米/小时，故选项A符合题意；乙车出发小时时距离A地千米，乙车速度是千米/小时，故选项B不合题意； 甲车第小时到达地，甲车的速度是千米/小时，则甲车到达地用时小时，则甲车在第小时出发，由图像可得甲，乙两车在第小时相遇，则甲车出发小时两车相遇，故选项正确；甲车行驶千米时，乙车行驶了千米，甲车先到B地，故选项D不合题意； 故选：【点睛】本题主要考查了函数图象信息分析，解答本题的关键是明确题意，利用数形结合的思想解答．5、A【解析】【分析】直接利用已知运算公式公式得出b的值，进而代入求出x=3时对应的值．【详解】解：∵输入x的值是4时，输出的y的值为7，∴7=2×4+b，解得：b=-1，若输入x的值是2，则输出的y的值是：y=-1×2+3=1．故选：A．【点睛】此题主要考查了函数值，正确得出b的值是解题关键．6、D【解析】【分析】根据函数三种表示方法的特点即可作出判断．【详解】前三个选项的叙述均正确，只有选项D的叙述是错误的，例如一天中的气温随时间的变化是一个函数关系，但此函数关系是无法用函数解析式表示的． 故选：D【点睛】本题考查了函数的三种表示方法，知道三种表示方法的特点是本题的关键．7、B【解析】【分析】根据甲、乙函数图像一个是直线一个不是直线即可判断①；根据甲从t=0开始出发，乙从t=0.5出发即可判断②③；根据甲、乙函数图像的交点的横坐标小于5可以判断④．【详解】解：由函数图像可知，甲的函数图像是一条直线，乙的函数图像不是直线，故甲是匀速运动，乙不是匀速运动，故①正确；乙在第0.5小时出发，在第5小时到达，则乙的行进时间为5-0.5=4.5小时，故②错误；根据函数图像可知乙比甲迟出发0.5小时，故③正确，根据函数图像可知，当乙追上甲时，两人的行进路程相同，即在函数图像中的甲、乙函数图像的交点处乙追上甲，则乙追上甲时，甲出发的时间小于5小时，故④错误；故选B．【点睛】本题主要考查了从函数图像获取信息，解题的关键在于能够准确读懂函数图像．8、A【解析】【分析】先作出合适的辅助线，再证明△ADC和△AOB的关系，即可建立y与x的函数关系，从而确定函数图像．【详解】解：由题意可得：OB＝x，OA＝1，∠AOB＝90°，∠BAC＝90°，AB＝AC，点C的纵坐标是y，作AD∥x轴，作CD⊥AD于点D，如图所示：∴∠DAO＋∠AOD＝180°，∴∠DAO＝90°，∴∠OAB＋∠BAD＝∠BAD＋∠DAC＝90°，∴∠OAB＝∠DAC，在△OAB和△DAC中， ∴△OAB≌△DAC（AAS），∴OB＝CD，∴CD＝x，∵点C到x轴的距离为y，点D到x轴的距离等于点A到x的距离1，∴y＝x＋1（x＞0）．故选：A．【点睛】本题考查动点问题的函数图象，明确题意、建立相应的函数关系式是解答本题的关键．9、A【解析】【分析】由图象所给信息对结论判断即可．【详解】由图象可知当x=0时，甲、乙两人在A、B两地还未出发故A，B之间的距离为1200m故①正确前12min为甲、乙的速度和行走了1200m故由图象可知乙用了24-4=20min走完了1200m则则故②正确又∵两人相遇时停留了4min∴两人相遇后从16min开始继续行走，由图象x=24时的拐点可知，到24min乙到达目的地则两人相遇后行走了24-16=8min，两人之间的距离为8×100=800米则b=800故③正确从24min开始为甲独自行走1200-800=400m则t=min故a=24+10=34故④正确综上所述①②③④均正确，共有四个结论正确．故选：A．【点睛】本题考查了从函数图象获取信息，运用数形结合的思想是解题的关键．10、C【解析】【分析】直接把y=5代入y=2x+1，解方程即可．【详解】解：当y=5时，5=2x+1，解得：x=2，故选：C．【点睛】本题考查了函数值，解题的关键是掌握已知函数解析式，给出函数值时，求相应的自变量的值就是解方程．二、填空题1、          【解析】【分析】由图象可知，当时，，可知；根据函数解析式自变量的取值范围可以知道，结合图象可以知道函数的取不到的值大概是在1的位置，所以大概预测可以得约为1，也即．【详解】解：由图象可知，当时，，；，结合图象可以知道函数的取不到的值大概是在1的位置，．故答案为：，．【点睛】本题考查函数的图象，解题的关键是能够通过已学的反比例函数图象确定的取值．2、单价【解析】【分析】常量是指在变化过程中，数值始终不变的量【详解】解：加油过程中，单价×数量=总价，此时，单价是常量，数量和金额是变量．故答案为：单价【点睛】本题考查常量的定义，牢记相关的知识点是解题关键．3、3【解析】【分析】由图2可知，当到P与C重合时最大，△ABP的面积最大，此时可求得BC=2；然后可知当P在CD上移动时面积不变，可知CD＝5-2＝3，因此可求△BCD的面积．【详解】解：动点P从直角梯形ABCD的直角顶点B出发，沿BC，CD的顺序运动，则△ABP面积y在BC段随x的增大而增大；在CD段，△ABP的底边不变，高不变，因而面积y不变化．由图2可以得到：BC=2，CD=3，△BCD的面积是×2×3=3．故答案为：3．【点睛】本题考查了动点问题的函数图象，理解问题，弄清题意，能够通过图象知道随自变量的增大，函数值是增大还是减小是解题的关键．4、图象【解析】略5、     速度×时间     时间t     路程s     速度60km/h     60 t     s     t【解析】略三、解答题1、（1），；（2）；（3），；（4）；（5），【解析】【分析】小明离家的距离y是时间x的函数，由图象中有两段平行于x轴的线段可知，小明离家后有两段时间先后停留在食堂与图书馆里，由此结合图形分析即可解答．【详解】解：（1）由纵坐标看出，食堂离小明家；由横坐标看出，小明从家到食堂用了．（2）由横坐标看出，，小明吃早餐用了．（3）由纵坐标看出，，食堂离图书馆；由横坐标看出，，小明从食堂到图书馆用了．（4）由横坐标看出，，小明读报用了．（5）由纵坐标看出，图书馆离小明家；由横坐标看出，，小明从图书馆回家用了，由此算出平均速度是．【点睛】本题考查的是函数图象的读图能力．要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件，结合题意正确计算是解题的关键．2、（1）7时，12时；（2）0～7时，12～24时上海气温高，7～12时上海气温低【解析】【分析】(1)根据题意，上海与北京气温相同就是函数图象中重合的部分，就可得出答案；(2)上海比北京气温高就是上海的图象在北京图象的上方，根据图象，就可得出答案；上海比北京气温低就是上海的图象在北京图象的下方，根据图象，就可得出答案．【详解】解：(1) 根据图象，可得到上海和北京在7时和12时，图象重合，故这一天内，上海与北京7时和12时气温相同．(2)根据图象，上海的图象在北京图象的上方的时间段为：0时至7时和12时至24时，故0时到7时和12时到24时，上海的气温比北京的高；根据图象，可得到7时至12时，上海的图象在北京的下方，故7时至12时，上海的气温比北京低．【点睛】本题考查函数图象，做题的关键是从函数图象中得到有效信息，分析解答即可．3、 (1)-4≤x≤3(2)-2≤y≤4(3)1；-2(4)-2≤x≤1【解析】【分析】根据自变量的定义，函数值的定义以及函数的最值和增减性，观察函数图象分别写出即可．(1)根据图像观察可得：自变量x的取值范围是-4≤x≤3；(2)根据图像观察可得：函数y的取值范围是-2≤y≤4；(3)根据图像观察可得：当x为1时，函数值最大；当x为-2时，函数值最小；(4)根据图像观察可得：当y随x的增大而增大时，x的取值范围是-2≤x≤1．【点睛】本题考查了函数的性质、函数图象，熟练掌握函数自变量的定义，函数值的定义以及函数的增减性并准确识图是解题的关键．4、，【解析】【分析】分别把华氏温度代入关系式计算即可得到答案．【详解】解：将代入中，解得：，将代入中，解得：，所以伦敦和纽约的温度换算成摄氏温度为：摄氏度，摄氏度．【点睛】本题考查了函数值的求解，将自变量的值代入函数关系式中即可，解题的关键是计算正确．5、（1）100℃；（2）温度，时间，时间，温度【解析】【分析】（1）根据表格中的数据求解即可；（2）观察表格可知，反映的是温度随时间的变化而变化由此即可得到答案．【详解】解：（1）观察表格可知：第8分钟时水的温度为100℃；（2）观察表格可知反映的是温度随着时间的变化而变化的，时间是自变量，温度是因变量；故答案为（1）100℃；（2）温度，时间，时间，温度．【点睛】本题主要考查了用表格表示变量之间的关系，解题的关键在于能够熟练掌握自变量与因变量的定义．