八年级下册第二十章 函数综合与测试课后作业题

这是一份八年级下册第二十章 函数综合与测试课后作业题，共27页。试卷主要包含了如图，点A的坐标为等内容，欢迎下载使用。
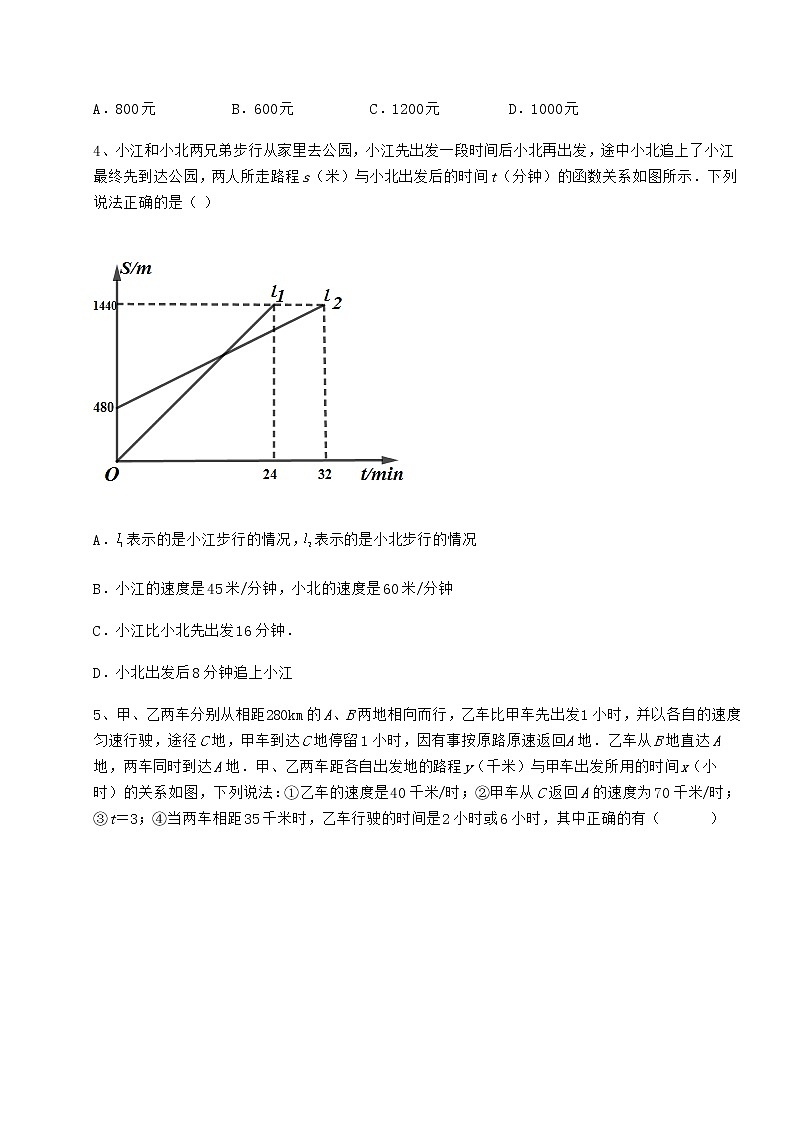
冀教版八年级数学下册第二十章函数难点解析 考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。第I卷（选择题  30分）一、单选题（10小题，每小题3分，共计30分）1、下列关系中，一定能称是x的函数的是（     ）A．y2＝4x B．|y|＝x－2 C．y＝|x|－3 D．y4＝64x2、某天，小南和小开两兄弟一起从家出发到某景区旅游，开始大家一起乘坐时速为50千米的旅游大巴，出发2小时后，小南有急事需回家，于是立即下车换乘出租车，一个小时后返回家中，办事用了30分钟后自己驾车沿同一路线以返回时的速度赶往景区，结果小南比小开早30分钟到达景区（三车的速度近似匀速，上下车的时间忽略不计，两地之间为直线路程），两人离家的距离y（千米）与出发时间x（小时）的关系如图所示，则以下说法错误的是（       ）A．出租车的速度为100千米/小时 B．小南追上小开时距离家300千米C．小南到达景区时共用时7.5小时 D．家距离景区共400千米3、某商场降价销售一批名牌球鞋，已知所获利润y（元）与降价金额x（元）之间满定函数关系式y＝﹣x2＋50x＋600，若降价10元，则获利为（       ）A．800元 B．600元 C．1200元 D．1000元4、小江和小北两兄弟步行从家里去公园，小江先出发一段时间后小北再出发，途中小北追上了小江最终先到达公园，两人所走路程s（米）与小北出发后的时间t（分钟）的函数关系如图所示．下列说法正确的是（ ）A．表示的是小江步行的情况，表示的是小北步行的情况B．小江的速度是45米/分钟，小北的速度是60米/分钟C．小江比小北先出发16分钟．D．小北出发后8分钟追上小江5、甲、乙两车分别从相距280km的A、B两地相向而行，乙车比甲车先出发1小时，并以各自的速度匀速行驶，途径C地，甲车到达C地停留1小时，因有事按原路原速返回A地．乙车从B地直达A地，两车同时到达A地．甲、乙两车距各自出发地的路程y（千米）与甲车出发所用的时间x（小时）的关系如图，下列说法：①乙车的速度是40千米/时；②甲车从C返回A的速度为70千米/时；③t＝3；④当两车相距35千米时，乙车行驶的时间是2小时或6小时，其中正确的有（       ）A．1个 B．2个 C．3个 D．4个6、如图，正方形ABCD的边长为4，P为正方形边上一动点，它沿A→D→C→B→A的路径匀速移动，设P点经过的路径长为x，△APD的面积是y，则下列图象能大致反映变量y与变量x的关系图象的是(       )A． B．C． D．7、下列各表达式不是表示y是x的函数的是（             ）A． B．C． D．8、如图，点A的坐标为（0，1），点B是x轴正半轴上的一动点，以AB为边作等腰直角ABC，使∠BAC＝90°，如果点B的横坐标为x，点C的纵坐标为y，那么表示y与x的函数关系的图像大致是（       ）A． B．C． D．9、下列曲线中，表示y是x的函数的是（       ）A． B．C． D．10、如图所示的图象（折线ABCDE）描述了一辆汽车在某一直线上的行驶过程中，汽车离出发地的距离s（千米）与行驶时间t（小时）之间的函数关系，根据图中提供的信息，给出下列说法：①汽车共行驶了140千米；②汽车在行驶途中停留了1小时；③汽车在第4小时到6小时的速度是25千米／时；④汽车出发后9小时返回原地．其中正确的说法共有（   ）A．1个 B．2个 C．3个 D．4个第Ⅱ卷（非选择题  70分）二、填空题（5小题，每小题4分，共计20分）1、若球体体积为，半径为，则．其中变量是_______、_______，常量是________．2、在函数中，自变量的取值范围是______．3、学校“青春礼”活动当天，小明和妈妈以不同的速度匀速从家里前往学校，小明害怕集合迟到先出发2分钟，随后妈妈出发，妈妈出发几分钟后，两人相遇，相遇后两人以小明的速度匀速前进，行进2分钟后，通过与妈妈交谈，小明发现忘记穿校服，于是小明立即掉头以原速度的2倍跑回家中，妈妈速度减半，继续匀速赶往学校，小明到家后，花了3分钟换校服，换好校服后，小明再次从家里出发，并以返回时的速度跑回学校，最后小明和妈妈同时到达学校．小明和妈妈之间的距离y与小明出发时间x之间的关系如图所示．则小明家与学校之间的距离是_____米．4、函数，当自变量时，函数值为______．5、在一条笔直的公路上有A、B两地，甲骑自行车从A地到B地；乙骑自行车从B地到A地，到达A地后立即按原路返回，如图是甲、乙两人离B地的距离y（km）与行驶时间x（h）之间的函数图象，若两人之间保持的距离不超过4km时，能够用无线对讲机保持联系，则甲、乙两人总共有________h可以用无线对讲机保持联系．三、解答题（5小题，每小题10分，共计50分）1、在初中阶段的函数学习中，我们经历了列表、描点、连线画函数图象，并结合图象研究函数性质及其应用的过程．以下是我们研究函数的性质及其应用的部分过程．请按要求完成下列各小题．（1）请把表补充完整，并在给出的图中补全该函数的大致图像；（2）请根据这个函数的图像，写出该函数的一条性质；（3）已知函数的图象如图所示，结合你所画的函数图象，直接写出不等式的解集．（近似值保留一位小数，误差不超过0．2）……-5-4-3-202345…………-14   ……2、公交公司员工小明住在站点的员工宿舍，每天早上去站点上班，站到站唯一一条公交线路示意图如图1，、、、是四个公交站点，其中、两站相距的路程是1200米，为了健身，小明往往沿公交线路步行到站或站后再乘公交车上班．（1）星期一，小明步行到站上车，记他距站的路程为米，离开站的时间为分，关于的函数图象如图2，求的解析式及公交车的速度；（2）星期二，小明以与星期一相同出发时间和步行速度步行到站上车，已知公交车无论上行（→）还是下行（→）都每隔10分钟一班，每天始发时间和行车速度保持不变，乘客上下车时间忽略不计；①通过计算判断小明步行到达站时是否恰好有上行公交车到达站；②小明到达站所用时间是星期一的1.5倍，求、两站相距的路程；③若小明步行至站时刚好遇见一辆下行班车，这一趟上班途中，直接写出他遇到下行班车的最短间隔时间．3、如图，在等边△ABC中，BC＝5cm，点D是线段BC上的一动点，连接AD，过点D作DE⊥AD，垂足为D，交射线AC与点E．设BD为xcm，CE为ycm．小聪根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．下面是小聪的探究过程，请补充完整：（1）通过取点、画图、测量，得到了x与y的几组值，如表：x/cm00.511.522.533.544.55y/cm5.03.32.01.10.4　 　0.30.40.30.20补全表格上相关数值．（2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；（3）结合画出的函数图象，解决问题：当线段BD是线段CE长的2倍时，BD的长度约为 　 　cm．4、图中的折线表示一骑车人离家的距离y与时间x的关系．骑车人9:00离开家，15:00回家．请你根据这个折线图回答下列问题：（1）这个人何时离家最远？这时他家多远？（2）何时他开始第一次休息？休息多长时间？这时他离家多远？（3）11:00～12:30他骑了多少千米？（4）他在9:00～10:30和10:30～12:30的平均速度各是多少？（5）他返家时的平均速度是多少？（6）14:00时他离家多远？何时他距家？5、在初中阶段的函数学习中，我们经历了列表、描点、连线画函数图象，并结合图象研究函数性质的过程．以下是我们研究函数的性质及其应用的部分过程，请按要求完成下列各小题．x……-4-3-2-101234567……y……a4b……（1）请直接写出上述表中、的值：a＝　     　，b＝　     　；（2）请在给出的图中补全该函数的大致图象；（3）请根据这个函数的图象，写出该函数的一条性质：　   　        ；（4）已知函数的图象如图所示，在的范围内，请直接不等式的解集：　　  　   ．（保留一位小数，误差不超过0.2）． -参考答案-一、单选题1、C【解析】【分析】根据函数的定义可知，满足对于x的每一个取值，y都有唯一确定的值与之对应关系，据此即可确定函数．【详解】解：根据函数概念可得：在一个变化过程中有两个变量x与y，对于x的每一个确定的值，y都有唯一的值与其对应可得C中y是x的函数，故选：C．【点睛】此题主要考查了函数的概念，关键是掌握函数的定义：在一个变化过程中，有两个变量x，y，对于x的每一个取值，y都有唯一确定的值与之对应，则y是x的函数，x叫自变量．2、B【解析】【分析】先根据旅游大巴2小时行2×50=100千米，出租车1小时行驶100千米，出租车速度可判断A正确；设小南t小时追上小开，利用两者距离相等列方程 50（2+1+0.5+t）=100t，解得t=3.5，可判断B不正确；利用到旅游区两者距离相等列方程50（2+1+0.5+t+0.5）=100t，解得t=4，可判断C正确；利用自驾车行驶速度×时间=100×4=400千米，可求出家距离景区共400千米，可判断D正确．【详解】解：旅游大巴2小时行2×50=100千米，出租车1小时行驶100千米，出租车速度为100÷1=100千米/时，故选项A正确；设小南t小时追上小开，50（2+1+0.5+t）=100t，解得t=3.5，∴100×3.5=350千米，故选项B不正确；50（2+1+0.5+t+0.5）=100t，解得t=4，∴小南到达景区时共用2+1+0.5+4=7.5小时，故选项C正确；∵100×4=400千米，∴家距离景区共400千米，故选项D正确．故选B．【点睛】本题考查函数图像信息获取与处理，掌握函数图像信息获取与处理方法是解题关键．3、D【解析】【分析】将代入函数关系式即可得．【详解】解：将代入得：，即获利为1000元，故选：D．【点睛】本题考查了求函数的函数值，熟练掌握函数值的求法是解题关键．4、C【解析】【分析】观察图象，可得：表示的是小北步行的情况，表示的是小江步行的情况，可得A错误；小江32分钟步行（1440-480）米，小北24分钟步行1440米，再根据该时间段内的速度等于路程除以时间，可得B错误；因为小江比小北先走480米，所以用480除以小江的速度30，可得C正确；设小北出发后 分钟追上小江，则 ，解出可得D错误，即可求解．【详解】解：根据题意得：A、因为小江先出发一段时间后小北再出发，所以表示的是小北步行的情况，表示的是小江步行的情况，故本选项不符合题意；B、小江的速度是米/分钟，小北的速度是米/分钟，故本选项不符合题意；C、观察图象，得：小江比小北先出发 分钟，故本选项符合题意；D、设小北出发后 分钟追上小江，则 ，解得： ，即小北出发后16分钟追上小江，故本选项不符合题意；故选：C【点睛】本题主要考查了函数图象的应用，准确从函数图象获取信息是解题的关键．5、B【解析】【分析】由乙车比甲车先出发1小时，与出发地的距离为千米，可判断①，由 千米/时，可判断②，由小时，可得可判断③，利用检验的方法计算当乙车行驶的时间是2小时或6小时时，两车相距的路程可判断④，从而可得答案.【详解】解：由函数图象可得：乙车比甲车先出发1小时，与出发地的距离为千米，所以乙车速度为：35千米/时，故①不符合题意；乙车行驶280千米需要的时间为：小时，所以甲车返回的速度为：千米/时，故②符合题意；由小时，所以 故③符合题意，当乙车行驶2小时时，行驶的路程为：千米，此时甲车行驶1小时，千米，所以两车相距：千米，当乙车行驶6小时时，行驶的路程为千米，距离A地70千米，此时甲车行驶了4个小时，行驶的路程为千米，此时在返回A地的路上，距离A地千米，所以两车相距千米，故④不符合题意；综上：故选B【点睛】本题考查的是从函数图象中获取信息，理解点的坐标含义，特别是利用检验的方法判断④，可以化繁为简，都是解本题的关键.6、B【解析】【分析】根据动点P的正方形各边上的运动状态分类讨论△APD的面积即可；【详解】由点P运动状态可知，当0≤x≤4时，点P在AD上运动，△APD的面积为0；当4≤x≤8时，点P在DC上运动，△APD的面积y＝×4×（x﹣4）＝2x﹣8；当8≤x≤12时，点P在CB上运动，△APD的面积y＝8；当12≤x≤16时，点P在BA上运动，△APD的面积y＝×4×（16﹣x）＝﹣2x+32；故选B．【点睛】本题主要考查了正方形的性质，动点问题与函数图象结合，准确分析计算是解题的关键．7、C【解析】略8、A【解析】【分析】先作出合适的辅助线，再证明△ADC和△AOB的关系，即可建立y与x的函数关系，从而确定函数图像．【详解】解：由题意可得：OB＝x，OA＝1，∠AOB＝90°，∠BAC＝90°，AB＝AC，点C的纵坐标是y，作AD∥x轴，作CD⊥AD于点D，如图所示：∴∠DAO＋∠AOD＝180°，∴∠DAO＝90°，∴∠OAB＋∠BAD＝∠BAD＋∠DAC＝90°，∴∠OAB＝∠DAC，在△OAB和△DAC中， ∴△OAB≌△DAC（AAS），∴OB＝CD，∴CD＝x，∵点C到x轴的距离为y，点D到x轴的距离等于点A到x的距离1，∴y＝x＋1（x＞0）．故选：A．【点睛】本题考查动点问题的函数图象，明确题意、建立相应的函数关系式是解答本题的关键．9、C【解析】【分析】根据函数的定义进行判断即可．【详解】解：在某一变化过程中，有两个变量x、y，一个量x变化，另一个量y随之变化，当x每取一个值，另一个量y就有唯一值与之相对应，这时，我们把x叫做自变量，y是x的函数，只有选项C中图象所表示的符合函数的意义，故选：C．【点睛】本题考查函数的定义，理解函数的定义，理解自变量与函数值的对应关系是正确判断的前提．10、C【解析】【分析】根据函数图像上的特殊点以及函数图像自身的实际意义进行判断即可．【详解】解：由图象可知，汽车走到距离出发点140千米的地方后又返回出发点，所以汽车共行驶了280千米，故①错误；从3时开始到4时结束，时间在增多，而路程没有变化，说明此时在停留，停留了4-3=1小时，故②正确；汽车在第4小时到6小时的速度是＝千米／时，故③正确；由图象可知，当t=9时，s=0，汽车出发后9小时返回原地，故④正确．∴正确的说法有：②③④，共有3个．故选：C．【点睛】此题考查了函数图像问题，解题的关键是正确分析题目中信息进行求解．二、填空题1、               【解析】【分析】根据函数常量与变量的知识点作答．【详解】∵函数关系式为，∴是自变量，是因变量，是常量．故答案为：，，．【点睛】本题考查了常量与变量的知识，解题关键是熟记变量是指在程序的运行过程中随时可以发生变化的量．2、全体实数【解析】【分析】根据整式函数的自变量不受限制即可求解【详解】解：∵函数是整式函数，自变量不受限制，∴自变量x的取值范围是全体实数．故答案为全体实数．【点睛】本题考查函数自变量的取值范围，掌握整式函数不受限制，分式函数要求分母不为0，根式函数要求被开方式有意义，零指数函数要求底数不为0是解题关键．3、1760【解析】【分析】根据函数图象可知，小明出发2分钟后走了160米，据此可得小明原来的速度，进而得出小明回时的速度．【详解】解：小明离家2分钟走了160米，∴小明初始速度为160÷2＝80米/分；小明返回家速度为80×2＝160米/分，妈妈继续行进速度80÷2＝40米/分；小明在家换衣服3分钟时间，妈妈走了40×3＝120米，设小明换好衣服离开家到与妈妈同时到达学校的时间为t分，则有160t＝1200+120+40t，∴t＝11，∴小明离家距离为11×160＝1760米．故答案为：1760米．【点睛】本题主要是考查了从函数图像获取信息，解题的关键是根据题意正确分析出函数图像中的数据．4、【解析】【分析】将函数的自变量的值代入函数解析式计算即可求解．【详解】解：将代入可得，，解得．故答案为：18．【点睛】本题考查了二次函数的定义，解题的关键是将自变量的值代入函数解析式并准确计算．5、【解析】【分析】根据题意可得A、B两地的距离为40千米；从而得到甲的速度为10千米/时，乙的速度为 20千米/时；然后设x小时后，甲、乙两人相距4km，可得到当 或 时，甲、乙两人可以用无线对讲机保持联系，即可求解．【详解】解：根据题意得：当x=0时，甲距离B地40千米，∴A、B两地的距离为40千米；由图可知，甲的速度为40÷4=10千米/时，乙的速度为40÷2=20千米/时；设x小时后，甲、乙两人相距4km，若是相遇前，则10x+20x=40-4，解得：x=1.2；若是相遇后，则10x+20x=40+4，解得： ；若是到达B地前，则10x-20（x-2）=4，解得：x=3.6∴当 或 时，甲、乙两人可以用无线对讲机保持联系，即甲、乙两人总共有 可以用无线对讲机保持联系．故答案为：【点睛】本题主要考查了函数图象，能够从图形获取准确信息是解题的关键．三、解答题1、（1）见解析；（2）当时，随的增大而增大﹔当时，随的增大而减小﹔当时，随的增大而减小﹔（3）或【解析】【分析】（1）由题意利用函数解析式分别求出对应的函数值即可；进而利用描点法画出图象即可；（2）根据题意观察图象可知该函数图象的增减性，以此进行分析即可；（3）根据题意直接利用图象即可解决问题．【详解】解：（1）…-5-4-3-202345……-1421… 补全图象如下：（2）当时，随的增大而增大﹔当时，随的增大而减小﹔当时，随的增大而减小﹔（3）由图象可知不等式的解集为：或.【点睛】本题考查函数图象和性质，能够从表格中获取信息，利用描点法画出函数图象，并结合函数图象解题是关键．2、（1） 公交车的速度为：米分；（2）①小明步行到达站时恰好有上行公交车到达站；②、两站相距的路程是6600米；③分钟【解析】【分析】（1）由图象上点可得小明步行的速度，从而可得函数解析式；由点的含义可得公交车的速度；（2）①先计算小明步行到达站需要分，再计算上行公交车到达站需要分，而，从而可得小明步行到达站时恰好有上行公交车到达站；②设小明星期一所用时间为，星期二到达站所用时间为，可得，，再利用列方程，再解方程即可得到答案；③由每隔10分钟一班，每辆公交车相距米，而步行的速度小于坐车时的速度，可得最短时间间隔发生在坐车时，从而可得答案.【详解】解：（1）由图象可知，小明步行的速度为（米分），的解析式为，公交车的速度为（米分）；（2）①小明步行到达站需要（分，上行公交车到达站需要（分，，小明步行到达站时恰好有上行公交车到达站；②设小明星期一所用时间为，星期二到达站所用时间为，由题可知，，小明到达站所用时间是星期一的1.5倍，，解得，、两站相距的路程是6600米；③每隔10分钟一班，每辆公交车相距（米，步行的速度小于坐车时的速度，最短时间间隔发生在坐车时，间隔时间为（分钟）．【点睛】本题考查的是从函数图象中获取信息，列函数关系式，一元一次方程的应用，理解题意与理解函数图象上点的坐标含义是解题的关键.3、（1）0；（2）见详解；（3）1.7【解析】【分析】（1）由题意认真按题目要求测量BD、CE,进行填表即可；（2）根据题意按照表格描点作图即可；（3）由题意线段BD是线段CE长的2倍的条件可以转化为一次函数图象，通过数形结合解决问题．【详解】解：（1）根据题意测量约0，故答案为：0；（2）根据题意画图：（3）当线段BD是线段CE长的2倍时，得到y=x图象，该图象与（2）中图象的交点即为所求情况，测量得BD长约1.7cm.故答案为：1.7.【点睛】本题考查函数作图和学生函数图象实际意义的理解，同时考查学生由数量关系得到函数关系的转化思想．4、（1）12:30～13:30，；（2）10:30，，；（3）；（4），；（5）；（6），14:30【解析】【分析】（1）直接观察图象，即可求解；（2）直接观察图象，即可求解；（3）用12：30时对应的距离减去11:00对应的距离，即可求解；（4）根据平均速度等于该时间段的路程除以时间，即可求解；（5）根据平均速度等于该时间段的路程除以时间，即可求解；（6）可先求出14：00到15：00的1小时内的平均速度，可得他距家时，从14:00所骑的路程，即可求解．【详解】解：（1）由图可知，这个人12：30-13：30时，离家最远，这时他离家45km；（2）由图可知，10：30时他开始第一次休息，从10：30到11:00，共休息了0.5h，这时他离家30km；（3）11：00~12：30他骑了45-30=15km；（4）他在9：00-10：30的1.5小时内的平均速度为：30÷1.5=20km/h，10：30~12：30的2小时内的平均速度为：（45-30）÷2=7.5km/h；（5）由图象可得：他返家时间为从13：30到15：00，共1.5h，45÷1.5=30km/h，即他返家时的平均速度是30km/h；（6）由图可知，14：00时他离家18km14：00到15：00的1小时内的平均速度为：18÷1=18km/h，（18-9）÷18=0.5h，即回家路上，14：30时他离家9km．【点睛】本题主要考查了函数图象的意义，能准确从函数图象获取信息是解题的关键．5、（1），；（2）图像见解析；（3）函数图像与x轴没有交点，且函数值都大于0（答案不唯一）；（4）【解析】【分析】（1）将x=0，3分别代入解析式即可得y的值，即可求出a、b的值；（2）描点、连线即可；（3）观察函数图象即可求得；（4）观察函数图像，先确定的范围内的交点，再由上下位置比较大小即可．【详解】（1）把代入解析式得；把代入解析式得故答案为：，；（2）函数图像如图：（3）由函数图像可知：函数图像与x轴没有交点，且函数值都大于0（答案不唯一）（4）由图象可知：在的范围内的解集为．【点睛】本题主要考查函数的图象和性质，会用描点法画出函数图象，利用数形结合的思想得到函数的性质是解题的关键．