八年级下册第二十二章 四边形综合与测试课后作业题

八年级数学下册第二十二章四边形综合测评

 考试时间：90分钟；命题人：数学教研组

考生注意：

1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟

2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上

3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题  30分）

一、单选题（10小题，每小题3分，共计30分）

1、如图，平面直角坐标系xOy中，点A是直线上一动点，将点A向右平移1个单位得到点B，点C（1，0），则OB＋CB的最小值为（       ）

A． B． C． D．

2、下列说法不正确的是（       ）

A．三角形的外角大于每一个与之不相邻的内角

B．四边形的内角和与外角和相等

C．等边三角形是轴对称图形，对称轴只有一条

D．全等三角形的周长相等，面积也相等

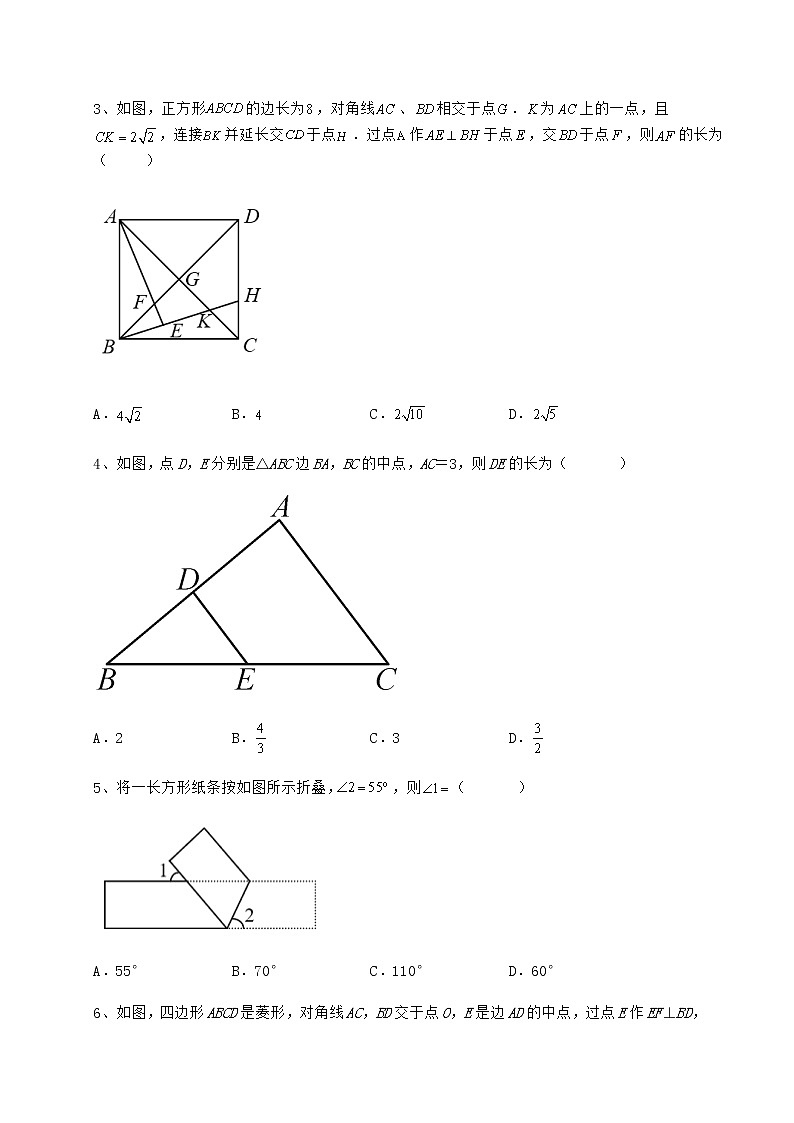
3、如图，正方形的边长为，对角线、相交于点．为上的一点，且，连接并延长交于点．过点作于点，交于点，则的长为（     ）

A． B． C． D．

4、如图，点D，E分别是△ABC边BA，BC的中点，AC＝3，则DE的长为（       ）

A．2 B． C．3 D．

5、将一长方形纸条按如图所示折叠，，则（       ）

A．55° B．70° C．110° D．60°

6、如图，四边形ABCD是菱形，对角线AC，BD交于点O，E是边AD的中点，过点E作EF⊥BD，EG⊥AC，点F，G为垂足，若AC=10，BD=24，则FG的长为（       ）

A． B．8 C． D．

7、一个多边形的内角和等于它的外角和的2倍，则这个多边形的边数是（       ）

A．5 B．4 C．7 D．6

8、平面上六个点A，B，C，D，E，F，构成如图所示的图形，则∠A＋∠B＋∠C＋∠D＋∠E＋∠F度数是（       ）

A．135度 B．180度 C．200度 D．360度

9、下列说法正确的是（　　）

A．只有正多边形的外角和为360°

B．任意两边对应相等的两个直角三角形全等

C．等腰三角形有两条对称轴

D．如果两个三角形一模一样，那么它们形成了轴对称图形

10、在平行四边形ABCD中，∠A ∶∠ B ∶∠ C ∶∠ D的值可以是（       ）

A．1∶2∶3∶4 B．1∶2∶2∶1 C．2∶2∶1∶1 D．1∶2∶1∶2

第Ⅱ卷（非选择题  70分）

二、填空题（5小题，每小题4分，共计20分）

1、如图，已知AD为的高，，以AB为底边作等腰，，交AC于F，连ED，EC，有以下结论：①；②；③；④；其中正确的是___．

2、矩形的性质定理1：矩形的四个角都是________．

符号语言：

∵四边形ABCD是矩形，

∴∠A＝∠B＝∠C＝∠D＝90°．

矩形的性质定理2：矩形的对角线________．

符号语言：

∵四边形ABCD是矩形，

∴AC ＝ BD．

3、如图，AC是正五边形ABCDE的对角线，则为______度．

4、如图，∠EAD和∠DCF是四边形ABCD的外角，∠EAD的平分线AG和∠DCF的平分线CG相交于点G．若∠B＝m°，∠D＝n°，则∠G＝______°．（用含m、n的代数式表示）

5、如图所示，是长方形地面，长，宽，中间竖有一堵砖墙高．一只蚂蚱从点爬到点，它必须翻过中间那堵墙，则它至少要走______的路程．

三、解答题（5小题，每小题10分，共计50分）

1、如图，在中，点D、E分别是边的中点，过点A作交的延长线于F点，连接，过点D作于点G．

(1)求证：四边形是平行四边形：

(2)若．

①当___________时，四边形是矩形；

②若四边形是菱形，则________．

2、如图，正方形ABCD和正方形CEFG，点G在CD上，AB＝5，CE＝2，T为AF的中点，求CT的长．

3、已知正多边形的内角和比外角和大720°，求该正多边形所有对角线的条数．

4、（1）【探究一】如图1，我们可以用不同的算法来计算图形的面积．

①方法1：如果把图1看成一个大正方形，那么它的面积为      ；

②方法2：如果把图1看成是由2个大小不同的正方形和2个大小相同的小长方形组成的图形，那么它的面积为      ；（写成关于a、b的两次三项式）用两种不同的算法计算同一个图形的面积，可以得到等式      ．

（2）【探究二】如图2，从一个顶点处引n条射线，请你数一数共有多少个锐角呢?

①方法1：一路往下数，不回头数．

以OA1为边的锐角有∠A1OA2、∠A1OA3、∠A1OA4、…、∠A1OAn，共有（n－1）个；

以OA2为边的锐角有∠A2OA3、∠A2OA4、…、∠A2OAn，共有（n－2）个；

以OA3为边的锐角有∠A3OA4、…、∠A3OAn，共有（n－3）个；

以OAn－1为边的锐角有∠An－1OAn，共有1个；

则图中锐角的总个数是      ；

②方法2：每一条边都能和除它以外的（n－1）条边形成锐角，共有n条边，可形成n（n－1）个锐角，但所有锐角都数了两遍，所以锐角的总个数是      ；

用两种不同的方法数锐角个数，可以得到等式      ．

（3）【应用】分别利用【探究一】中得到的等式和【探究二】中运用的思想解决问题．

①计算：19782＋20222；

②多边形中连接任意两个不相邻顶点的线段叫做对角线，如五边形共有5条对角线，则十七边形共有      条对角线，n边形共有      条对角线．

5、如图，矩形ABCD的对角线AC、BD相交于点O，AB＝5cm，∠BOC＝120°，求矩形对角线的长．

-参考答案-

一、单选题

1、A

【解析】

【分析】

设D（﹣1，0），作D点关于直线的对称点E，连接OE，交直线于A，连接AD，，作ES⊥x轴于S，根据题意OE就是OB＋CB的最小值，由直线的解析式求得F的坐标，进而求得ED的长，从而求得OS和ES，然后根据勾股定理即可求得OE．

【详解】

解：设D（﹣1，0），作D点关于直线的对称点E，连接OE，交直线于A，连接AD，，交于点，作ES⊥x轴于S，

∵AB∥DC，且AB＝OD＝OC＝1，

∴四边形ABOD和四边形ABCO是平行四边形，

∴AD＝OB，OA＝BC，

∴AD＋OA＝OB＋BC，

∵AE＝AD，

∴AE＋OA＝OB＋BC，

即OE＝OB＋BC，

∴OB＋CB的最小值为OE，

由，

当时，，

解得：，

，

，

当时，，

，

，

，

取的中点，过作轴的垂线交于，

，

当时，，

，

，

，

为的中点，

，

为等边三角形，

，

，

，

，

∴FD＝3，∠FDG＝60°，

∴DG＝DF＝，

∴DE＝2DG＝3，

∴ES＝DE＝，DS＝DE＝，

∴OS＝，

∴OE＝＝，

∴OB＋CB的最小值为，

故选：A．

【点睛】

本题考查了一次函数的性质，轴对称﹣最短路线问题以及平行四边形的性质、勾股定理的应用，解题的关键是证得OE是OB+CB的最小值．

2、C

【解析】

【分析】

根据三角形外角的性质，四边形内角和定理和外角和定理，等边三角形的对称性，全等三角形的性质判断即可．

【详解】

∵三角形的外角大于每一个与之不相邻的内角，正确，

∴A不符合题意；

∵四边形的内角和与外角和都是360°，

∴四边形的内角和与外角和相等，正确，

∴B不符合题意；

∵等边三角形是轴对称图形，对称轴有三条，

∴等边三角形是轴对称图形，对称轴只有一条，错误，

∴C符合题意；

∵全等三角形的周长相等，面积也相等，正确，

∴D不符合题意；

故选C．

【点睛】

本题考查了三角形外角的性质，四边形的内角和，外角和定理，等边三角形的对称性，全等三角形的性质，准确相关知识是解题的关键．

3、C

【解析】

【分析】

根据正方形的性质以及已知条件求得的长，进而证明，即可求得，勾股定理即可求得的长

【详解】

解：如图，设的交点为，

四边形是正方形

，,

，，

，,

在与中

在中，

故选C

【点睛】

本题考查了正方形的性质，勾股定理，全等三角形的性质与判定，掌握正方形的性质是解题的关键．

4、D

【解析】

略

5、B

【解析】

【分析】

从折叠图形的性质入手，结合平行线的性质求解．

【详解】

解：由折叠图形的性质结合平行线同位角相等可知，，

，

．

故选：B．

【点睛】

本题考查折叠的性质及平行线的性质，解题的关键是结合图形灵活解决问题．

6、A

【解析】

【分析】

由菱形的性质得出OA=OC=5，OB=OD=12，AC⊥BD，根据勾股定理求出AD=13，由直角三角形斜边上的中线等于斜边的一半求出OE=6.5，证出四边形EFOG是矩形，得到EO=GF即可得出答案．

【详解】

解：连接OE，

∵四边形ABCD是菱形，

∴OA=OC=5，OB=OD=12，AC⊥BD，

在Rt△AOD中，AD==13，

又∵E是边AD的中点，

∴OE=AD=×13=6.5，

∵EF⊥BD，EG⊥AC，AC⊥BD，

∴∠EFO=90°，∠EGO=90°，∠GOF=90°，

∴四边形EFOG为矩形，

∴FG=OE=6.5．

故选：A．

【点睛】

本题考查了菱形的性质、矩形的判定与性质、直角三角形斜边上中线定理等知识；熟练掌握菱形的性质和矩形的性质是解题的关键．

7、D

【解析】

【分析】

利用多边形内角和公式和外角和定理，列出方程即可解决问题．

【详解】

解：根据题意，得：（n-2）×180=360×2，

解得n=6．

故选：D．

【点睛】

本题考查了多边形内角与外角，解答本题的关键是根据多边形内角和公式和外角和定理，利用方程法求边数．

8、D

【解析】

【分析】

根据三角形外角性质及四边形内角和求解即可．

【详解】

解：如下图所示：

根据三角形的外角性质得，∠1=∠C+∠E，∠2=∠B+∠D，

∵∠1+∠2+∠A+∠F=360°，

∴∠A+∠B+∠C+∠D+∠E+∠F=360°，

故选：D．

【点睛】

此题考查了三角形的外角性质，熟记三角形外角性质及四边形内角和为360°是解题的关键．

9、B

【解析】

【分析】

选项A根据多边形的外角和定义判断即可；选项B根据三角形全等的判定方法判断即可；选项C根据轴对称图形的定义判断即可；选项D根据轴对称的性质判断即可．

【详解】

解：A．所有多边形的外角和为，故本选项不合题意；

B．任意两边对应相等的两个直角三角形全等，说法正确，故本项符合题意；

C．等腰三角形有1条对称轴，故本选项不合题意；

D．如果两个三角形一模一样，那么它们不一定形成轴对称图形，故本选项不合题意；

故选：B．

【点睛】

此题主要考查了多边形的外角和，轴对称的性质，等腰三角形的性质，全等三角形的判定，解题的关键是掌握轴对称图形的概念．

10、D

【解析】

略

二、填空题

1、①③

【解析】

【分析】

只要证明，，是的中位线即可一一判断；

【详解】

解：如图延长交于，交于．设交于．

，，

，

，，

，故①正确，

，，

，

，

，

不垂直，故②错误，

，

，

，，

，

，

是等腰直角三角形，平分，

，

，

，

，

，故③正确，

，

，

，

，

，故④正确．

故答案是：①③．

【点睛】

本题考查等腰直角三角形的性质和判定、全等三角形的判定和性质、三角形中位线定理等知识，解题的关键是正确寻找全等三角形解决问题，属于中考选择题中的压轴题．

2、     直角     相等

【解析】

略

3、72

【解析】

【分析】

先根据正五边形的内角和求出它的每个内角的度数，再根据等腰三角形的性质可得的度数，然后根据角的和差即可得．

【详解】

解：五边形是正五边形，

，

，

，

故答案为：72．

【点睛】

本题考查了正多边形的性质、等腰三角形的性质等知识点，熟练掌握正多边形的性质是解题关键．

4、

【解析】

【分析】

根据四边形的内角和定理可得 ，从而得到，再由∠EAD的平分线AG和∠DCF的平分线CG相交于点G．可得，进而得到，再根据 ，即可求解．

【详解】

解：∵∠B＝m°，∠D＝n°，

∴ ，

∵∠EAD和∠DCF是四边形ABCD的外角，

∴ ，

∵∠EAD的平分线AG和∠DCF的平分线CG相交于点G．

∴ ，

∴ ，

∵ ，

∴ ．

故答案为：

【点睛】

本题主要考查了多边形的内角和定理，角平分线的应用，补角的应用，熟练掌握多边形的内角和定理是解题的关键．

5、

【解析】

【分析】

根据题意，将长方形底面和中间墙展开为平面图，并连接BD，根据两点之间直线段最短和勾股定理的性质计算，即可得到答案．

【详解】

将长方形底面和中间墙展开后的平面图如下，并连接BD

根据题意，展开平面图中的

∴一只蚂蚱从点爬到点，最短路径长度为展开平面图中BD长度

∵是长方形地面

∴

∴

故答案为：．

【点睛】

本题考查了立体图形展开图、矩形、两点之间直线段最短、勾股定理的知识；解题的关键是熟练掌握立体图形展开图、勾股定理的知识，从而完成求解．

三、解答题

1、 (1)见解析；

(2)①3；②

【解析】

【分析】

（1）根据三角形中位线的性质得到DEAB，BD=CD，即可证得四边形ABDF是平行四边形，得到AF=BD=CD，由此得到结论；

（2）①由点D、E分别是边BC、AC的中点，得到DE=AB，由四边形是平行四边形，得到DF=2DE=AB=3，再根据矩形的性质得到AC=DF=3；

②根据菱形的性质得到DF⊥AC，推出AB⊥AC，利用勾股定理求出AC，得到CE，利用面积法求出答案．

(1)

证明：∵点D、E分别是边BC、AC的中点，

∴DEAB，BD=CD，

∵，

∴四边形ABDF是平行四边形，

∴AF=BD=CD，

∴四边形是平行四边形；

(2)

解：①∵点D、E分别是边BC、AC的中点，

∴DE=AB，

∵四边形是平行四边形，

∴DF=2DE=AB=3，

∵四边形是矩形,

∴AC=DF=3，

故答案为：3；

②∵四边形是菱形，

∴DF⊥AC，

∵DEAB，

∴AB⊥AC，

∴AD=BC=2.5，

∴AE=EC=2，

∵

∴

∴，

故答案为：．

【点睛】

此题考查了平行四边形的判定及性质，矩形的性质，菱形的性质，三角形中位线的判定及性质，勾股定理，是一道较为综合的几何题，熟练掌握各知识点并应用是解题的关键．

2、

【解析】

【分析】

连接AC，CF，如图，根据正方形的性质得到AC=，AB=5，CF=CE=2，∠ACD=45°，∠GCF=45°，则利用勾股定理得到AF=，然后根据直角三角形斜边上的中线性质得到CT的长．

【详解】

解：连接AC、CF，如图，

∵四边形ABCD和四边形CEFG都是正方形，

∴AC=AB=5，CF=CE=2，∠ACD=45°，∠GCF=45°，

∴∠ACF=45°+45°=90°，

在Rt△ACF中，

∵T为AF的中点，

∴，

∴CT的长为．

【点睛】

本题考查了正方形的性质：正方形的四条边都相等，四个角都是直角；正方形的两条对角线相等，互相垂直平分，并且每条对角线平分一组对角；正方形具有四边形、平行四边形、矩形、菱形的一切性质，也考查了直角三角形斜边上的中线性质．

3、20条

【解析】

【分析】

多边形的内角和可以表示成（n-2）•180°，外角和是固定的360°，根据正多边形内角和与外角和的差等于720°，列方程求出正多边形的边数．然后根据n边形共有条对角线，得出此正多边形的所有对角线的条数．

【详解】

解：设此正多边形为正n边形．

由题意得：，

解得n＝8，

∴此正多边形所有的对角线条数为：＝20．

答：这个正多边形的所有对角线有20条．

【点睛】

此题考查多边形的边数与对角线条数,一元一次方程，解题关键在于掌握多边形内角和公式和外角和，以及对角线条数计算公式.．

4、（1）①；②；=；（2）①（n－1）＋（n－2）＋（n－3）＋……＋1；②；（n－1）＋（n－2）＋（n－3）＋……＋1=；（3）①8000968；②119，n(n-3)

【解析】

【分析】

（1）①根据边长为(a+b)的正方形面积公式求解即可；

②利用矩形和正方形的面积公式求解即可；

（2）①根据题中的数据求和即可；

②根据题意求解即可；

（3）①利用（1）的规律求解即可；

②根据n边形从一个顶点出发可引出（n-3）条对角线．从n个顶点出发引出（n-3）条，而每条重复一次，所以n边形对角线的总条数为n(n-3)（n≥3，且n为整数）可得答案．

【详解】

解：（1）①大正方形的面积为；

②由2个大小不同的正方形和2个大小相同的小长方形组成的图形的面积为；

可以得到等式：=；

故答案为：①；②；=；

（2）①图中锐角的总个数是：（n－1）＋（n－2）＋（n－3）＋……＋1；

②锐角的总个数是n（n－1）；

可以得到等式为（n－1）＋（n－2）＋（n－3）＋……＋1=n（n－1）；

故答案为：①（n－1）＋（n－2）＋（n－3）＋……＋1；②n（n－1）；（n－1）＋（n－2）＋（n－3）＋……＋1=n（n－1）；

（3）①19782＋20222＝[2000＋（－22）]2＋（2000＋22）2

＝20002＋（－22）2＋2×2000×（－22）＋20002＋222＋2×2000×22

＝2×（20002＋222）

＝2×[4000000＋（20＋2）2]

＝2×[4000000＋（202＋22＋2×20×2）]＝8000968；

②一个四边形共有2条对角线，即×4×(4-3)=2；

一个五边形共有5条对角线，即×5×(5-3)=5；

一个六边形共有9条对角线，即×6×(6-3)=9；

……，

一个十七边形共有×17×(17-3)=119条对角线；

一个n边形共有n(n-3)（n≥3，且n为整数）条对角线．

故答案为：119，n(n-3)．

【点睛】

本题考查了图形的变化规律，完全平方公式，多边形的对角线，对于这种图形的变化规律的问题，读懂题目信息，找到变化规律是解题的关键．

5、10cm

【解析】

【分析】

根据矩形性质得出∠ABC＝90°，AC＝BD，OA＝OC＝AC，OB＝OD＝BD，推出OA＝OB，求出等边三角形AOB，求出OA＝OB＝AB＝5，即可得出答案．

【详解】

解：∵∠BOC＝120°，

∴∠AOB＝180°﹣120°＝60°，

∵四边形ABCD是矩形，

∴∠ABC＝90°，AC＝BD，OA＝OC＝AC，OB＝OD＝BD，

∴OA＝OB，

∵∠AOB＝60°，

∴△AOB是等边三角形，

∵AB＝5cm，

∴OA＝OB＝AB＝5cm，

∴AC＝2AO＝10cm，BD＝AC＝10cm．

【点睛】

本题考查了矩形的性质和等边三角形的性质和判定的应用，解此题的关键是求出OA、OB的长，题目比较典型，是一道比较好的题目．