2022届高三二轮专题卷 数学（十一）直线、平面垂直的判定与性质 教师版

这是一份2022届高三二轮专题卷 数学（十一）直线、平面垂直的判定与性质 教师版，共22页。试卷主要包含了如图，在四棱锥中，，，等内容，欢迎下载使用。
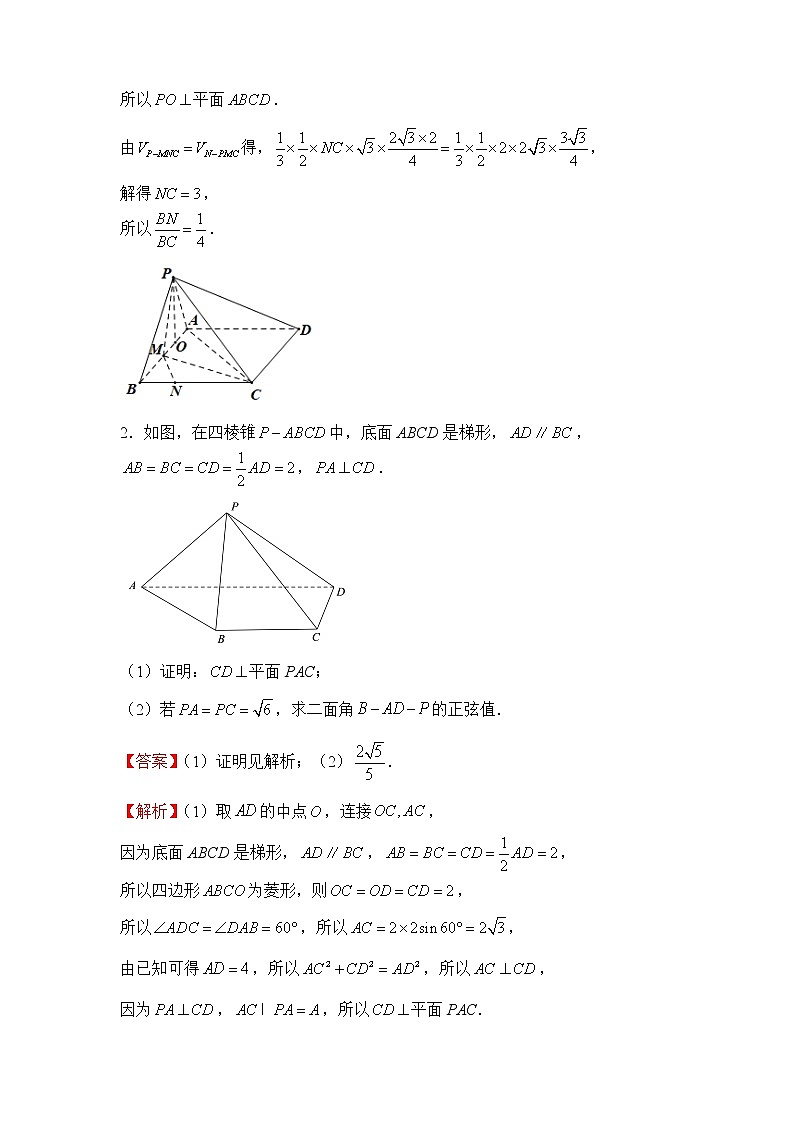
   1．直线与平面垂直的判定定理和性质定理1．如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，，，，，点M是AB的中点，点N是线段BC上的动点．（1）证明：平面PAB；（2）若点N到平面PCM的距离为，求的值．【答案】（1）证明见解析；（2）．【解析】（1）证明：连接AC，在中，因为，，，所以，因为，，所以是等边三角形．因为点是的中点，所以，在中，，，，满足，所以，而，所以平面．（2）过点作，垂足为，由（1）可知平面，因为平面，所以平面平面，平面平面，所以平面．由得，，解得，所以．2．如图，在四棱锥中，底面ABCD是梯形，，，．（1）证明：平面PAC；（2）若，求二面角的正弦值．【答案】（1）证明见解析；（2）．【解析】（1）取的中点，连接，因为底面ABCD是梯形，，，所以四边形为菱形，则，所以，所以，由已知可得，所以，所以，因为，，所以平面PAC．（2）因为，，所以，所以为等腰直角三角形，由（1）知，平面，平面，所以平面平面，取的中点，连接，则，因为平面平面，平面，所以平面，连接，以为坐标原点，分别以所在的直线为轴建立空间直角坐标系，则，所以，设平面的一个法向量为，则，令，则，平面的一个法向量为，所以，所以二面角的正弦值为．3．如图，在四棱锥中，，，．（1）证明：平面；（2）在下面三个条件中选择两个条件：________，求点到平面的距离．①；②二面角为；③直线与平面成角为．【答案】（1）证明见解析；（2）答案见解析．【解析】（1）取的中点为，连接，可知四边形是平行四边形，所以，所以点在以为直径的圆上，所以，又，且平面，所以平面．（2）选①②因为平面，所以，又因为，所以二面角的平面角为，所以，又因为，所以为等边三角形，因为平面，平面，所以平面平面，连接交于点，则为的中点，连接，则，因为平面平面，平面平面，所以平面，所以，由题意可知，，所以，故以点为坐标原点建立如下图所示的空间直角坐标系，，则，设平面的法向量为，由，得，令，则，点到平面的距离为．选①③因为平面，平面，所以平面平面，易知为在平面内的射影，即为与平面所成的角，即，又因为，所以为等边三角形．连接交于点，则为的中点，连接，则，因为平面平面，平面平面，所以平面，所以，由题意可知，，所以，故以点为坐标原点建立如下图所示的空间直角坐标系，，则，设平面的法向量为，由，得，令，则，点到平面的距离为．选②③因为平面，平面，所以平面平面，易知为在平面内的射影，即为与平面所成的角，即，因为平面，所以，又因为，所以二面角的平面角为，所以，所以为等边三角形．连接交于点，则为的中点，连接，则，因为平面平面，平面平面，所以平面，所以，由题意可知，，所以，故以点为坐标原点建立如下图所示的空间直角坐标系，，则，设平面的法向量为，由，得，令，则，点到平面的距离为．4．如图，在三棱锥中，平面平面，是以为斜边的等腰直角三角形，，，O为AC的中点，M为内部或边界上的动点，且平面．（1）证明：；（2）设直线PM与平面ABC所成角为，求的最小值．【答案】（1）证明见解析；（2）．【解析】（1）证明：在三棱锥中，连接OB，OP，因为是以AC为斜边的等腰直角三角形，，O为AC中点，所以，，又，所以平面POB，因为平面POB，所以．（2）由（1）知，平面平面ABC，平面平面，平面PAC，所以平面ABC．又，分别以OB，OC，OP所在直线为x轴，y轴、z轴建立空间直角坐标系，则，，，，设，则，，，，．设平面的法向量为，则，即，令，则，同理可求得平面PBC的法向量．因为平面PAB，平面PBC，所以，即，即，所以．又，所以．所以，又平面，所以是平面ABC的一个法向量，所以，令，，所以，当，即时，取得最大值为，此时取得最小值为．注：也可以分别取PC，BC的中点E，F，先证明M在线段EF上．5．如图，在长方体中，，点在线段AB上．（1）证明：；（2）当点是AB中点时，求与平面所成角的大小．【答案】（1）证明见解析；（2）．【解析】（1）连接，因为在长方体中，所以有平面，平面，所以，又因为，所以四边形是正方形，所以，又，所以平面，又平面，所以．（2）以点为原点，所在直线为轴，所在直线为轴，所在直线为轴建立空间直角坐标系，则各点坐标为，，，，当点是AB中点时，可得，所以，，设为平面的一个法向量，则，即，令，可得，所以，又，所以，设与平面所成角为，，则，即，所以与平面所成的角为．6．如图，在四棱锥中，底面ABCD，底面ABCD是等腰梯形，，．（1）证明：；（2）求点C到平面PBD的距离．【答案】（1）证明见解析；（2）．【解析】（1）证明：如图，过点A作，垂足为E，连接AC，设AC与BD交于点O．因为底面ABCD是等腰梯形，，所以，．又，所以，．因为，所以，则，同理．因为，所以，即．因为底面ABCD，底面ABCD，所以．又，平面PAC，所以平面PAC．又平面PAC，所以．（2）解：由（1）可知，，，，所以．又平面ABCD，所以．因为，，所以，．在中，，所以，故．设点C到平面PBD的距离为d，因为，所以，解得，即点C到平面PBD的距离为． 2．平面与平面垂直的判定定理和性质定理1．在三棱锥中，平面平面，和都是边长为的等边三角形，若为三棱锥外接球上的动点，则点到平面距离的最大值为（    ）A． B． C． D．【答案】D【解析】设中点为，的外心为，的外心为，过点作平面的垂线，过点作平面的垂线，两条垂线的交点，则点即为三棱锥外接球的球心，因为和都是边长为的正三角形，可得，因为平面平面，，平面，平面平面，所以平面，又平面，所以，又，所以四边形是边长为1的正方形，所以外接球半径，所以到平面的距离，即点到平面距离的最大值为，故选D．2．如图，在直三棱柱中，，，F为棱上一点，，连接AF，．（1）证明：平面平面；（2）求平面与平面所成锐二面角的余弦值．【答案】（1）证明见解析；（2）．【解析】（1）如图，延长和CB的延长线相交于点E，连接AE，则AE为平面与底面ABC的交线，由已知得，，，所以，由AB、BC的长都为3，AC的长为，得，所以，在三角形ABE中，由余弦定理，得，所以，所以，即，又是直三棱柱，故平面ABC，又平面ABC，所以，因为，所以平面，又平面，所以平面平面．（2）以E为坐标原点，EC，EA所在直线分别为x轴、y轴，平行于的直线为z轴建立空间直角坐标系，则，，，，．设平面的法向量为，则，即，不妨设，由（1）得，，，，设平面的法向量为，则，即，不妨设，设平面与平面所成锐二面角为，则，所以平面与平面所成锐二面角的余弦值为．3．如图，在四棱锥中，四边形ABCD是边长为2的菱形，，，且．（1）证明：平面平面ABCD；（2）若，且线段SD上一点E满足平面AEC，求AE与平面SAB所成角的正弦值．【答案】（1）证明见解析；（2）．【解析】（1）证明：如图，取AD的中点O，连接SO，CO，AC．因为四边形ABCD是边长为2的菱形，，所以，且．则为正三角形，故，．因为，所以为直角三角形，所以．又因为，所以，所以．又因为，平面，所以平面．又因为平面ABCD，所以平面平面ABCD．（2）解：如图，连接BD，设AC，BD的交点为F．因为平面AEC，平面平面，所以，所以E为线段SD中点．因为，且O为AD中点，所以．又因为，且，AD，平面ABCD，所以平面ABCD．所以两两垂直，所以以为原点，以所在的直线分别为轴，建立空间直角坐标系，则，，，，，则，，．设平面SAB的法向量为，则，取，得，设AE与平面SAB所成角为，则．4．如图，在三棱柱中，侧面底面，为的中点，且．（1）求证：平面；（2）求点到平面的距离．【答案】（1）证明见解析；（2）．【解析】（1）证明：，且为的中点，，又侧面底面，平面平面，且平面，平面．（2）解：连接，则，且，因为平面，则，而，，，因为平面，平面，，所以，，因为，，，平面，且，故四边形为平行四边形，所以，，平面，平面，故，，设点到平面的距离为，由，得，，故点到平面的距离是．5．如图，在四棱锥中，平面平面，且是边长为2的等边三角形，四边形是矩形，，为的中点．（1）证明：；（2）求直线与平面所成的正弦值．【答案】（1）证明见解析；（2）．【解析】（1）取的中点，连接，，∵四边形是矩形，，，且，分别是，的中点，∴，，，，∴，，，∴，∴，∵是等边三角形，是的中点，∴，又平面平面，平面平面，平面，∴平面，又平面，∴，又，，，平面，∴平面，又平面，∴．（2）设直线与平面所成角为．连接，则，∵，，，∴，设到平面的距离为，则，∵，∴，故到平面的距离为．6．在四棱锥中，平面平面，，底面是梯形，，，，是边的中点．（1）证明：；（2）若平面与平面所成二面角为60°，求四棱锥的体积．【答案】（1）证明见解析；（2）．【解析】（1）在梯形中，，，∴，∴，∵平面平面，平面平面，平面，，∴平面，∴，即．（2）如图，建立空间直角坐标系，取的中点，因为，所以，因为平面平面，平面平面，所以平面，设，∴，，，，，，设平面的一个法向量，∴，令，可得，平面的一个法向量，∴，∴．