2020-2021学年第二十二章 四边形综合与测试优秀课堂检测

八年级数学下册第二十二章四边形专项攻克

 考试时间：90分钟；命题人：数学教研组

考生注意：

1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟

2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上

3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题  30分）

一、单选题（10小题，每小题3分，共计30分）

1、如图，在边长为的正方形ABCD中，点E是对角线AC上一点，且于点F，连接DE，当时，（　　　）

A．1 B． C． D．

2、下列命题错误的是（       ）

A．两组对边分别平行的四边形是平行四边形

B．两组对边分别相等的四边形是平行四边形

C．一组对边平行，另一组对边相等的四边形是平行四边形

D．对角线互相平分的四边形是平行四边形

3、如图，平行四边形ABCD的对角线AC，BD相交于点O，下列结论错误的是（　　）

A．AO＝CO B．AD∥BC C．AD＝BC D．∠DAC＝∠ACD

4、一个多边形从一个顶点引出的对角线条数是4条，这个多边形的边数是（       ）

A．5 B．6 C．7 D．8

5、如图，矩形中，，如果将该矩形沿对角线折叠，那么图中阴影部分的面积是22.5，则（       ）

A．8 B．10 C．12 D．14

6、下面性质中，平行四边形不一定具备的是（　　）

A．对角互补 B．邻角互补

C．对角相等 D．对角线互相平分

7、如图，在正方形ABCD中，AB＝3，点E，F分别在边AB，CD上，∠EFD＝60°．若将四边形EBCF沿EF折叠，点B′恰好落在AD边上，则BE的长度为（       ）

A．1 B． C． D．2

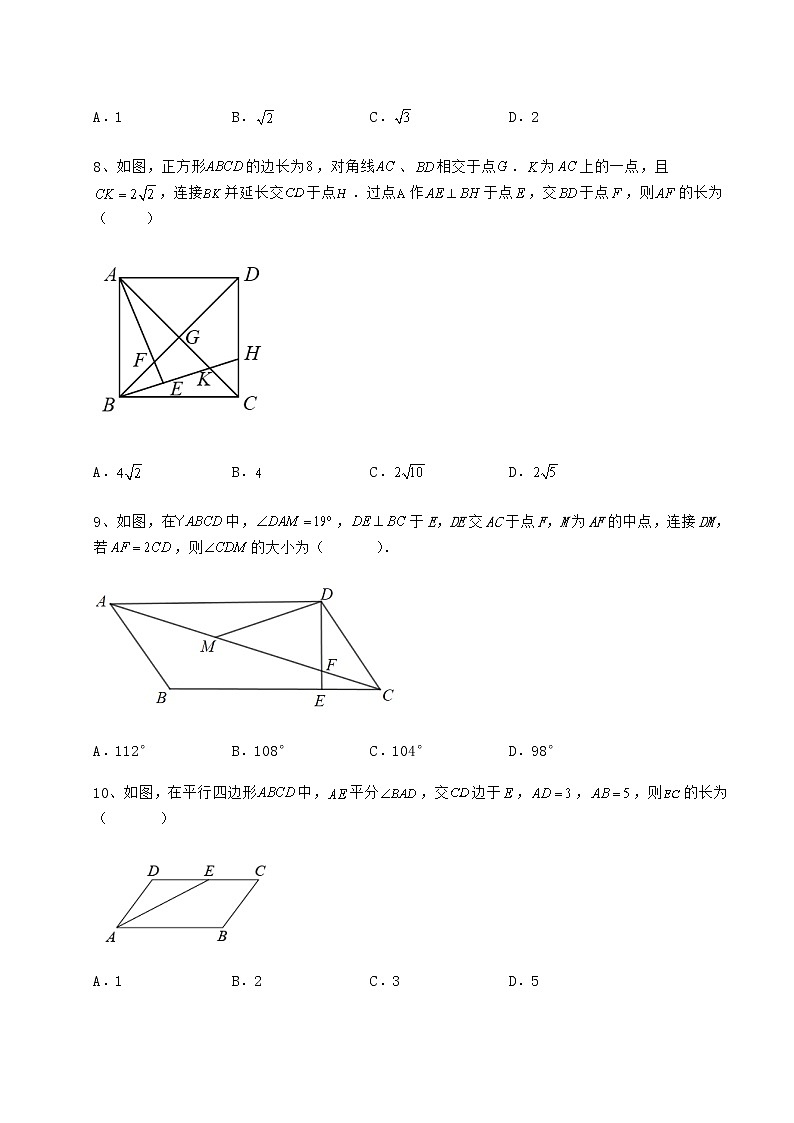
8、如图，正方形的边长为，对角线、相交于点．为上的一点，且，连接并延长交于点．过点作于点，交于点，则的长为（     ）

A． B． C． D．

9、如图，在中，，于E，DE交AC于点F，M为AF的中点，连接DM，若，则的大小为（       ）．

A．112° B．108° C．104° D．98°

10、如图，在平行四边形中，平分，交边于，，，则的长为（       ）

A．1 B．2 C．3 D．5

第Ⅱ卷（非选择题  70分）

二、填空题（5小题，每小题4分，共计20分）

1、如图，，D为外一点，且交的延长线于E点，若，则_______．

2、矩形的两边长分别为3 cm和4 cm，则矩形的对角线长为_____．

3、两组对边分别________的四边形叫做平行四边形．

4、平行四边形的性质：平行四边形的两组对边分别________；平行四边形的两组对角分别________；平行四边形的对角线________．

5、如图，正方形ABCD的边长为，作正方形A1B1C1D1，使A，B，C，D是正方形A1B1C1D1，各边的中点；做正方形A2B2C2D2，使A1，B1，C1，D1是正方形A2B2C2D2各边的中点…以此类推，则正方形A2021B2021C2021D2021的边长为 _____．

三、解答题（5小题，每小题10分，共计50分）

1、已知正方形与正方形，，．

(1)如图1，若点和点重合，点在线段上，点在线段的延长线上，连接、、，将阴影部分三角形的面积记作，则         （用含有、的代数式表示）．

(2)如图2，若点与点重合，点在线段上，点在线段的延长线上，连接、、，将阴影部分三角形的面积记作，则         （用含有、的代数式表示）．

(3)如图3，若将正方形沿正方形的边所在直线平移，使得点、在线段上（点不与点重合、点不与点重合），连接、、，设，将阴影部分三角形的面积记作，则         （用含有、、的代数式表示）．

(4)如图4，若将正方形沿正方形的边所在直线平移，使得点、在的延长线上，连接、、，设，将阴影部分三角形的面积记作，则         （用含有、、的代数式表示）．

2、（1）【发现证明】

如图1，在正方形中，点，分别是，边上的动点，且，求证：．小明发现，当把绕点顺时针旋转90°至，使与重合时能够证明，请你给出证明过程．

（2）【类比引申】

①如图2，在正方形中，如果点，分别是，延长线上的动点，且，则（1）中的结论还成立吗？若不成立，请写出，，之间的数量关系______（不要求证明）

②如图3，如果点，分别是，延长线上的动点，且，则，，之间的数量关系是______（不要求证明）

（3）【联想拓展】如图1，若正方形的边长为6，，求的长．

3、如图，正方形ABCD和正方形CEFG，点G在CD上，AB＝5，CE＝2，T为AF的中点，求CT的长．

4、如图，已知矩形ABCD（AB＜AD）．E是BC上的点，AE=AD．

(1)在线段CD上作一点F，连接EF，使得∠EFC＝∠BEA(请用直尺和圆规作图，保留作图痕迹)；

(2)在（1）作出的图形中，若AB＝4，AD＝5，求DF的值．

5、已知∠MON＝90°，点A是射线ON上的一个定点，点B是射线OM上的一个动点，点C在线段OA的延长线上，且AC＝OB．

(1)如图1，CDOB，CD＝OA，连接AD，BD．

①           ；

②若OA＝2，OB＝3，则BD＝           ；

(2)如图2，在射线OM上截取线段BE，使BE＝OA，连接CE，当点B在射线OM上运动时，求∠ABO和∠OCE的数量关系；

(3)如图3，当E为OB中点时，平面内一动点F满足FA=OA，作等腰直角三角形FQC，且FQ=FC，当线段AQ取得最大值时，直接写出的值．

-参考答案-

一、单选题

1、C

【解析】

【分析】

证明，则，计算的长，得，证明是等腰直角三角形，可得的长．

【详解】

解：四边形是正方形，

，，，

，

，

，

，

，

，

，

，

，

是等腰直角三角形，

，

故选：C．

【点睛】

本题考查正方形的性质，勾股定理，等腰直角三角形，三角形的外角的性质等知识，解题的关键是在正方形中学会利用等腰直角三角形的性质解决问题，属于中考常考题型．

2、C

【解析】

【分析】

根据平行四边形的判定逐项分析即可得．

【详解】

解：A、两组对边分别平行的四边形是平行四边形，正确，则此项不符合题意；

B、两组对边分别相等的四边形是平行四边形，正确，则此项不符合题意；

C、一组对边平行，另一组对边相等的四边形可能是平行四边形，也可能是等腰梯形，故原命题错误，此项符合题意；

D、对角线互相平分的四边形是平行四边形，正确，则此项不符合题意，

故选：C．

【点睛】

本题考查了平行四边形的判定，熟记平行四边形的判定是解题关键．

3、D

【解析】

【分析】

根据平行四边形的性质解答．

【详解】

解：∵四边形ABCD是平行四边形，

∴AO＝OC，故A正确；

∴，故B正确；

∴AD＝BC，故C正确；

故选：D．

【点睛】

此题考查了平行四边形的性质，熟记平行四边形的性质是解题的关键．

4、C

【解析】

【分析】

根据从n边形的一个顶点引出对角线的条数为(n-3)条，可得答案．

【详解】

解：∵一个n多边形从某个顶点可引出的对角线条数为(n-3)条，

而题目中从一个顶点引出4条对角线，

∴n-3=4，得到n=7，

∴这个多边形的边数是7．

故选：C．

【点睛】

本题考查了多边形的对角线，从一个顶点引对角线，注意相邻的两个顶点不能引对角线．

5、C

【解析】

【分析】

根据折叠和矩形的性质，可得∠DBE =∠CBD，AD∥BC，AD=BC，AB⊥AD，从而得到∠BDE=∠DBE，进而得到BE=DE，再由的面积是22.5，可得，然后根据勾股定理，即可求解．

【详解】

解：根据题意得： ∠DBE =∠CBD，AD∥BC，AD=BC，AB⊥AD，

∴∠BDE=∠CBD，

∴∠BDE=∠DBE，

∴BE=DE，

∵的面积是22.5，，

∴ ，解得： ，

∴，

在 中，由勾股定理得：

   ，

∴ ．

故选：C

【点睛】

本题主要考查了折叠和矩形的性质，勾股定理，熟练掌握折叠和矩形的性质，勾股定理是解题的关键．

6、A

【解析】

【分析】

直接利用平行四边形的性质：对角相等、对角线互相平分、对边平行且相等，进而分析得出即可．

【详解】

解：A、平行四边形对角不一定互补，故符合题意；

B、平行四边形邻角互补正确，故不符合题意；

C、平行四边形对角相等正确，故不符合题意．

D、平行四边形的对角线互相平分正确，故不符合题意；

故选A．

【点睛】

此题主要考查了平行四边形的性质，熟练掌握相关性质是解题关键．

7、D

【解析】

【分析】

由正方形的性质得出∠EFD=∠BEF=60°，由折叠的性质得出∠BEF=∠FEB'=60°，BE=B'E，设BE=x，则B'E=x，AE=3-x，由直角三角形的性质可得：2（3-x）=x，解方程求出x即可得出答案．

【详解】

解：∵四边形ABCD是正方形，

∴AB∥CD，∠A=90°，

∴∠EFD=∠BEF=60°，

∵将四边形EBCF沿EF折叠，点B'恰好落在AD边上，

∴∠BEF=∠FEB'=60°，BE=B'E，

∴∠AEB'=180°-∠BEF-∠FEB'=60°，

∴B'E=2AE，

设BE=x，则B'E=x，AE=3-x，

∴2（3-x）=x，

解得x=2．

故选：D．

【点睛】

本题考查了正方形的性质，折叠的性质，含30°角的直角三角形的性质等知识点，能综合性运用性质进行推理是解此题的关键．

8、C

【解析】

【分析】

根据正方形的性质以及已知条件求得的长，进而证明，即可求得，勾股定理即可求得的长

【详解】

解：如图，设的交点为，

四边形是正方形

，,

，，

，,

在与中

在中，

故选C

【点睛】

本题考查了正方形的性质，勾股定理，全等三角形的性质与判定，掌握正方形的性质是解题的关键．

9、C

【解析】

【分析】

根据平行四边形及垂直的性质可得为直角三角形，再由直角三角形中斜边上的中线等于斜边的一半可得，由等边对等角及三角形外角的性质得出，根据三角形内角和定理即可得出．

【详解】

解：∵四边形ABCD为平行四边形，

∴，

∵，

∴，

∴为直角三角形，

∵M为AF的中点，

∴，

∴，，

∵，

∴，

∴，

∴，

故选：C．

【点睛】

题目主要考查平行四边形的性质，直角三角形中斜边上的中线等于斜边的一半，等边对等角及三角形外角的性质和三角形内角和定理，理解题意，综合运用这些知识点是解题关键．

10、B

【解析】

【分析】

先由平行四边形的性质得，，再证，即可求解．

【详解】

解：四边形是平行四边形，

，，

，

平分，

，

，

，

，

故选：B．

【点睛】

本题考查了平行四边形的性质，等腰三角形的判定等知识，解题的关键是灵活应用这些知识解决问题．

二、填空题

1、2

【解析】

【分析】

过点D作DM⊥CB于M，证出∠DAE=∠DBM，判定△ADE≌△BDM，得到DM=DE=3，证明四边形CEDM是矩形，得到CE=DM=3，由AE=1，求出BC=AC=2．

【详解】

解：∵DE⊥AC，

∴∠E=∠C=90°，

∴，

过点D作DM⊥CB于M，则∠M=90°=∠E，

∵AD=BD，

∴∠BAD=∠ABD，

∵AC=BC，

∴∠CAB=∠CBA，

∴∠DAE=∠DBM，

∴△ADE≌△BDM，

∴DM=DE=3，

∵∠E=∠C=∠M =90°，

∴四边形CEDM是矩形，

∴CE=DM=3，

∵AE=1，

∴BC=AC=2，

故答案为：2．

【点睛】

此题考查了全等三角形的判定及性质，矩形的判定及性质，等边对等角证明角度相等，正确引出辅助线证明△ADE≌△BDM是解题的关键．

2、5cm

【解析】

略

3、平行

【解析】

略

4、     相等     相等     互相平分

【解析】

略

5、

【解析】

【分析】

根据勾股定理求得正方形对角线的长度，然后结合三角形中位线定理求得正方形的边长，从而探索数字变化的规律，进而求解．

【详解】

由题意得，正方形ABCD中

CD=AD=

在Rt△ACD中，

AC==2

∵A，B，C，D是正方形各边的中点，

∴正方形的边长为2=

在Rt△中

==2

∵是正方形各边中点

∴正方形的边长为2=      

以此类推

则正方形的边长为

故答案为：

【点睛】

本题考查勾股定理，正方形性质，探索数字变化的规律是解题关键．

三、解答题

1、 (1)

(2)

(3)

(4)

2、（1）见解析；（2）①不成立，结论：；②，见解析；（3）

【解析】

【分析】

（1）证明，可得出，则结论得证；

（2）①将绕点顺时针旋转至根据可证明，可得，则结论得证；②将绕点逆时针旋转至，证明，可得出，则结论得证；

（3）求出，设，则，，在中，得出关于的方程，解出则可得解．

【详解】

（1）证明：把绕点顺时针旋转至，如图1，

，，，

，

，，三点共线，

，

，

，

，

，

，

，

；

（2）①不成立，结论：；

证明：如图2，将绕点顺时针旋转至，

，，，，

，

，

，

；

②如图3，将绕点逆时针旋转至，

，，

，

，

，

，

，

，

．

即．

故答案为：．

（3）解：由（1）可知，

正方形的边长为6，

，

．

，

，

设，则，，

在中，

，

，

解得：．

，

．

【点睛】

本题属于四边形综合题，主要考查了正方形的性质、旋转的性质、全等三角形的判定与性质以及勾股定理的综合应用，解题的关键是作辅助线构造全等三角形，根据全等三角形的对应边相等进行推导．

3、

【解析】

【分析】

连接AC，CF，如图，根据正方形的性质得到AC=，AB=5，CF=CE=2，∠ACD=45°，∠GCF=45°，则利用勾股定理得到AF=，然后根据直角三角形斜边上的中线性质得到CT的长．

【详解】

解：连接AC、CF，如图，

∵四边形ABCD和四边形CEFG都是正方形，

∴AC=AB=5，CF=CE=2，∠ACD=45°，∠GCF=45°，

∴∠ACF=45°+45°=90°，

在Rt△ACF中，

∵T为AF的中点，

∴，

∴CT的长为．

【点睛】

本题考查了正方形的性质：正方形的四条边都相等，四个角都是直角；正方形的两条对角线相等，互相垂直平分，并且每条对角线平分一组对角；正方形具有四边形、平行四边形、矩形、菱形的一切性质，也考查了直角三角形斜边上的中线性质．

4、 (1)见解析

(2)

【解析】

【分析】

（1）作∠DAE的角平分线，与DC的交点即为所求，理由：可先证明△AEF≌△ADF，可得∠AEF=∠D=90°，从而得到∠DAE+∠DFE=180°，进而得到∠EFC=∠DAE，再由AD∥BC，即可求解；

（2）根据矩形的性质可得∠B＝∠C＝∠D＝90°，AD＝BC＝5，AB＝CD＝4，从而得到BE＝3，进而得到EC＝2，然后在 中，由勾股定理，即可求解．

(1)

解：如图，作∠DAE的角平分线，与DC的交点即为所求．

∵AE=AD，∠EAF=∠DAF，AF=AF，

∴△AEF≌△ADF，

∴∠AEF=∠D=90°，

∴∠DAE+∠DFE=180°，

∵∠EFC+∠DFE=180°，

∴∠EFC=∠DAE，

∵在矩形ABCD中，AD∥BC，

∴∠BEA=∠DAE，

∴∠EFC＝∠BEA；

(2)

解：∵四边形ABCD是矩形，

∴∠B＝∠C＝∠D＝90°，AD＝BC＝5，AB＝CD＝4，

∵AE＝AD＝5，

∴BE＝＝＝3，

∴EC＝BC﹣BE＝5﹣3＝2，

由（1）得：△AEF≌△ADF，

∴ ，

在 中， ，

∴ ，

∴ ．

【点睛】

本题主要考查了矩形的性质，全等三角形的判定和性质，勾股定理等知识，熟练掌握矩形的性质，全等三角形的判定和性质，勾股定理是解题的关键．

5、 (1)△DCA；

(2)∠ABO+∠OCE=45°，理由见解析

(3)

【解析】

【分析】

（1）①由平行线的性质可得∠ACD=∠BOA=90°，再由OB=CA，OA=CD，即可利用SAS证明△AOB≌△DCA；②过点D作DR⊥BO交BO延长线于R，由①可知△AOB≌△DCA，得到CD=OA=2，AC=OB=3，再由OC⊥OB，DR⊥OB，CD∥OB，得到DR=OC=OA+AC=5（平行线间距离相等），同理可得OR=CD=3，即可利用勾股定理得到；

（2）如图所示，过点C作CW⊥AC，使得CW=OA，连接AW，BW，先证明△AOB≌△WCA得到AB=AW，∠ABO=∠WAC，然后推出∠ABW=∠AWB=45°，证明四边形BECW是平行四边形，得到BW∥CE，则∠WJC=∠BWA=45°，由三角形外角的性质得到∠WJC=∠WAC+∠JCA，则∠ABO+∠OCE=45°；

（3）如图3-1所示，连接AF，则，如图3-2所示，当A、F、Q三点共线时，AQ有最大值，由此求解即可．

(1)

解：①∵CD∥OB，

∴∠ACD=∠BOA=90°，

又∵OB=CA，OA=CD，

∴△AOB≌△DCA（SAS）；

故答案为：△DCA；

②如图所示，过点D作DR⊥BO交BO延长线于R，

由①可知△AOB≌△DCA，

∴CD=OA=2，AC=OB=3，

∵OC⊥OB，DR⊥OB，CD∥OB，

∴DR=OC=OA+AC=5（平行线间距离相等），

同理可得OR=CD=3，

∴BR=OB+OR=5，

∴；

故答案为：；

(2)

解：∠ABO+∠OCE=45°，理由如下：

如图所示，过点C作CW⊥AC，使得CW=OA，连接AW，BW，

在△AOB和△WCA中，

，

∴△AOB≌△WCA（SAS），

∴AB=AW，∠ABO=∠WAC，

∵∠AOB=90°，

∴∠ABO+∠BAO=90°，

∴∠BAO+∠WAC=90°，

∴∠BAW=90°，

又∵AB=AW，

∴∠ABW=∠AWB=45°，

∵BE⊥OC，CW⊥OC，

∴BE∥CW，

又∵BE=OA=CW，

∴四边形BECW是平行四边形，

∴BW∥CE，

∴∠WJC=∠BWA=45°，

∵∠WJC=∠WAC+∠JCA，

∴∠ABO+∠OCE=45°；

(3)

解：如图3-1所示，连接AF，

∴，

∴如图3-2所示，当A、F、Q三点共线时，AQ有最大值，

∵E是OB的中点，BE=OA，

∴BE=OE=OA，

∴OB=AC=2OA，

∵△CFQ是等腰直角三角形，CF=QF，

∴∠CFQ=∠CFA=90°，

∴，

∴，

∴．

【点睛】

本题主要考查了全等三角形的性质与判定，勾股定理，平行四边形的性质与判定，平行线的性质与判定等等，熟知相关知识是解题的关键．