
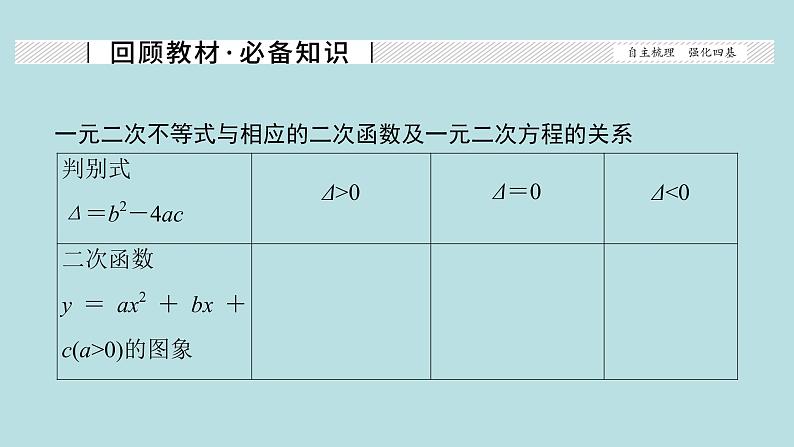





2022届高考数学理一轮复习新人教版课件:第六章不等式推理与证明第二节一元二次不等式及其解法
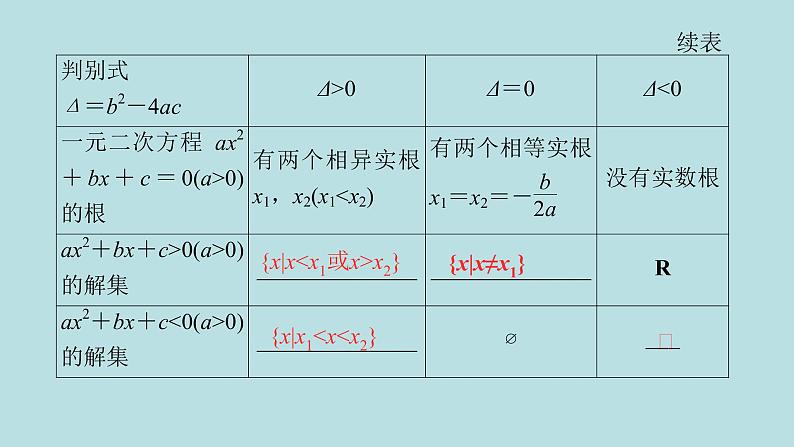
展开{x|x
{x|x1
3.(基本能力:求参数取值范围)已知不等式x2-2x+k2-1>0对一切实数x恒成立,则实数k的取值范围为_______________________.
[典例剖析]类型 1 解简单的一元二次不等式[例1] (1)(2020·高考全国卷Ⅰ)已知集合A={x|x2-3x-4<0},B={-4,1,3,5},则A∩B=( )A.{-4,1} B.{1,5}C.{3,5} D.{1,3}
题型一 一元二次不等式的解法
解析:∵A={x|x2-3x-4<0}={x|(x+1)(x-4)<0}={x|-1<x<4},B={-4,1,3,5},∴A∩B={1,3}.
(2)不等式-x2-3x+4>0的解集为_______________________.(用区间表示)解析:-x2-3x+4>0⇒(x+4)(x-1)<0.如图所示,作出函数y=(x+4)(x-1)的图象,∴当-4
(2)(2020·广东梅州模拟)关于x的不等式x2-(m+2)x+2m<0的解集中恰有3个正整数,则实数m的取值范围为( )A.(5,6] B.(5,6)C.(2,3] D.(2,3)解析:关于x的不等式x2-(m+2)x+2m<0可化为(x-m)(x-2)<0,∵该不等式的解集中恰有3个正整数,∴不等式的解集为{x|2<x<m},且5<m≤6,即实数m的取值范围是(5,6].
方法总结1.一元二次不等式的解集可依据一元二次方程的根及一元二次函数图象求得,当ax2+bx+c=0有两根x1、x2时,ax2+bx+c>0(a>0)的解集是“两根之外”型,ax2+bx+c<0(a>0)的解集是“两根之内”型.
2.对含参数的一元二次不等式,也要按此原理讨论:
[题组突破]1.(母题变式)将例1(2)的不等式改为“-x2-3x+4≤0”,其解集为________________________________________________.解析:由-x2-3x+4≤0得x2+3x-4≥0,即(x+4)(x-1)≥0,∴x≥1或x≤-4.
答案:(-∞,-4]∪[1,+∞)
2.(母题变式)将例1(2)的不等式变为“x2-3x+4>0”,其解集为________________________.解析:令y=x2-3x+4,∵Δ=(-3)2-4×4<0,y>0恒成立,∴x∈R.
4.解关于x的不等式ax2-(a+1)x+1<0(a>0).
类型 1 在R上恒成立问题[例1] 若不等式(a-2)x2+2(a-2)x-4<0对一切x∈R恒成立,则实数a的取值范围是( )A.(-∞,2] B.[-2,2]C.(-2,2] D.(-∞,-2)
题型二 不等式恒成立问题
类型 3 给定参数范围恒成立问题[例3] (1)对于任意a∈[-1,1],f(x)=x2+(a-4)x+4-2a的值恒大于0,那么x的取值范围是________.解析:令g(a)=x2+(a-4)x+4-2a=(x-2)a+x2-4x+4,由题意知g(-1)>0且g(1)>0,解得x<1或x>3.
答案:(-∞,1)∪(3,+∞)
(2)若mx2-mx-1<0对于m∈[1,2]恒成立,求实数x的取值范围.
2.给出参数范围解不等式,采用反解“主元法”,将参数视作“主元”,即将参数看作“自变量”的构造函数,建立不等式.
[题组突破]1.不等式a2+8b2≥λb(a+b)对于任意的a,b∈R恒成立,则实数λ的取值范围为________.解析:因为a2+8b2≥λb(a+b)对于任意的a,b∈R恒成立,所以a2+8b2-λb(a+b)≥0恒成立,即a2-λba+(8-λ)b2≥0恒成立,由二次不等式的性质可得Δ=λ2b2+4(λ-8)b2=b2(λ2+4λ-32)≤0,所以(λ+8)(λ-4)≤0,解得-8≤λ≤4.答案:[-8,4]
2.已知f(x)=mx2-mx-1,若对于x∈[1,3],f(x)<-m+5恒成立,则实数m的取值范围是________________________.
高考数学(文数)一轮复习课件 第六章 不等式、推理与证明 第一节 不等关系与不等式(含详解): 这是一份高考数学(文数)一轮复习课件 第六章 不等式、推理与证明 第一节 不等关系与不等式(含详解),共22页。
高考数学(文数)一轮复习课件 第六章 不等式、推理与证明 第二节 一元二次不等式及其解法(含详解): 这是一份高考数学(文数)一轮复习课件 第六章 不等式、推理与证明 第二节 一元二次不等式及其解法(含详解),共26页。
2022届高考数学理一轮复习新人教版课件:第六章不等式推理与证明第五节推理与证明: 这是一份2022届高考数学理一轮复习新人教版课件:第六章不等式推理与证明第五节推理与证明,共60页。PPT课件主要包含了类似特征,一般原理,特殊情况,假设Q不成立,第一个值n0,n=k+1,答案A,答案B,答案D,答案C等内容,欢迎下载使用。












