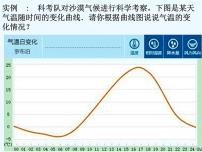




高中数学优质课《函数的单调性与最值》课件与教学设计2
展开问题1:观察函数的图象,解决下列问题:(1)图象有什么样的“升”、“降”规律?
f (x)=-2x+2
(2)图象的这种“升”、降”规律反映了随着自变量的 变化,函数值是如何变化的?
问题3:以二次函数 f(x)=x2 为例,如何用符号语言描述“f(x)在 上是增函数,即在 上,随着x的增大,相应的 f(x) 也随着增大?
一般地,设函数f(x)的定义域为I:
如果对于定义域I内某个区间D上的 两个自变量的值 ,当 时,都有 ,那么就说函数f(x)在区间D上是减函数.
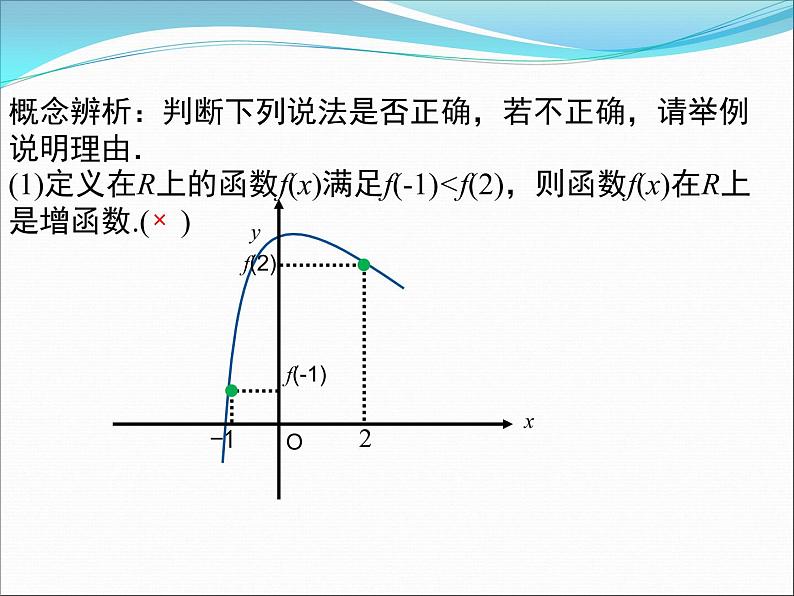
概念辨析:判断下列说法是否正确,若不正确,请举例说明理由.
(1)定义在R上的函数f(x)满足f(-1)
(3)反比例函数 在 上是减函数.( )
(4) 函数y=f(x)在 上是增函数,任取 如果 ,那么 ( )
例1 下图是定义在闭区间[-5, 5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一单调区间上, y=f(x)是增函数还是减函数.
解:函数y=f(x)的单调区间有
其中y=f(x)在[-5,-2),[1, 3)上是减函数,
在区间[-2, 1),[3, 5]
例2 试用单调性的定义证明函数 在 (0, +∞)上为增函数.
1. 任取:任取x1,x2 区间D,且x1
2. 判断:判断相应的f(x1)与f(x2)的大小;
3. 根据定义下结论:指出函数y=f(x)在给定区间D上的单调性.
x1,x2 的三个特征:任意性、同区间、有大小
练习 证明函数 在 上是减函数.
通过本节课的学习,我们来体会一下都有哪些收获?
统考版高中数学(文)复习2-2函数的单调性与最值课件: 这是一份统考版高中数学(文)复习2-2函数的单调性与最值课件,共55页。PPT课件主要包含了必备知识基础落实,增函数,减函数,上升的,下降的,单调区间,f′x0,fx≤M,fx0=M,fx≥M等内容,欢迎下载使用。
高中数学高考第2章 §2 2 函数的单调性与最值课件PPT: 这是一份高中数学高考第2章 §2 2 函数的单调性与最值课件PPT,共60页。PPT课件主要包含了落实主干知识,单调递增,单调递减,函数的最值,fx≤M,fx≥M,fx0=M,-∞0,探究核心题型,确定函数的单调性等内容,欢迎下载使用。
高中数学优质课《函数的单调性与最值》课件与教学设计1: 这是一份高中数学优质课《函数的单调性与最值》课件与教学设计1,文件包含《函数的单调性与最值》教学课件pptx、《函数的单调性与最值》教学设计docx、《函数的单调性与最值》教学点评doc等3份课件配套教学资源,其中PPT共17页, 欢迎下载使用。