

初中数学沪科版九年级下册第26章 概率初步综合与测试测试题
展开沪科版九年级数学下册第26章概率初步章节训练
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、下列事件是必然事件的是( )
A.明天一定是晴天 B.购买一张彩票中奖
C.小明长大会成为科学家 D.13人中至少有2人的出生月份相同
2、在不透明口袋内装有除颜色外完全相同的5个小球,其中红球2个,白球3个.搅拌均匀后,随机抽取一个小球,是红球的概率为( )
A. B. C. D.
3、下列事件中,属于不可能事件的是( )
A.射击运动员射击一次,命中靶心
B.从一个只装有白球和红球的袋中摸球,摸出黄球
C.班里的两名同学,他们的生日是同一天
D.经过红绿灯路口,遇到绿灯
4、不透明的布袋内装有形状、大小、质地完全相同的1个白球,2个红球,3个黑球,若随机摸出一个球恰是黑球的概率为( )
A. B. C. D.
5、布袋内装有1个黑球和2个白球,这些球除颜色外其余都相同,随机摸出一个球后不放回,再随机摸出一个球,则两次摸出的球都是白球的概率是( )
A. B. C. D.
6、养鱼池养了同一品种的鱼,要大概了解养鱼池中的鱼的数量,池塘的主人想出了如下的办法:“他打捞出80尾鱼,做了标记后又放回了池塘,过了三天,他又捞了一网,发现捞起的90尾鱼中,带标记的有6尾.”你认为池塘主的做法( )
A.有道理,池中大概有1200尾鱼 B.无道理
C.有道理,池中大概有7200尾鱼 D.有道理,池中大概有1280尾鱼
7、下列说法正确的是( )
A.“明天降雨的概率是80%”表示明天有80%的时间都在降雨
B.“抛一枚硬币正面朝上的概率为”表示每抛两次就有一次正面朝上
C.“彩票中奖的概率是1%”表示买100张彩票肯定会中奖
D.“抛一枚均匀的正方体骰子,朝上的点数是2的概率为”表示随着抛掷次数的增加,“拋出朝上的点数是2”这一事件发生的概率稳定在附近
8、成语“守株待兔”描述的这个事件是( )
A.必然事件 B.确定事件 C.不可能事件 D.随机事件
9、下列事件中是必然事件的是( )
A.小菊上学一定乘坐公共汽车
B.某种彩票中奖率为1%,买10000张该种票一定会中奖
C.一年中,大、小月份数刚好一样多
D.将豆油滴入水中,豆油会浮在水面上
10、不透明袋中装有3个红球和5个绿球,这些球除颜色外无其他差别.从袋中随机摸出1个球是红球的概率为( )
A. B. C. D.
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、第24届冬季奥林匹克运动会将于2022年2月4日在北京开幕,小健通过统计数据了解到:从2002年到2018年的五届冬奥会上,中国队每届比赛均有金牌入账,共斩获了13枚金牌,于是,小健对同学们说:“2022年北京冬奥会中国队获得2枚以上金牌的可能性大小是100%”.你认为小健的说法______(填“合理”或“不合理”)理由是______.
2、一个袋中有形状材料均相同的白球2个、红球3个,任意摸一个球是红球的概率_____.
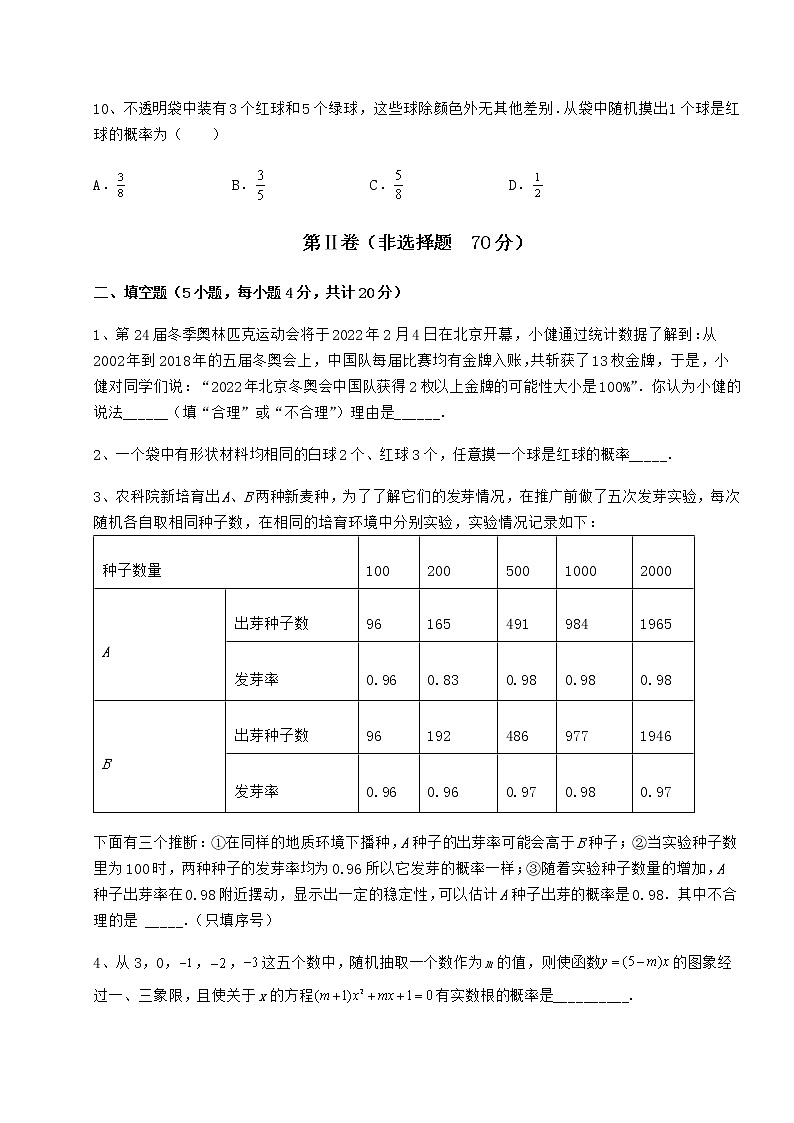
3、农科院新培育出A、B两种新麦种,为了了解它们的发芽情况,在推广前做了五次发芽实验,每次随机各自取相同种子数,在相同的培育环境中分别实验,实验情况记录如下:
种子数量 | 100 | 200 | 500 | 1000 | 2000 | |
A | 出芽种子数 | 96 | 165 | 491 | 984 | 1965 |
发芽率 | 0.96 | 0.83 | 0.98 | 0.98 | 0.98 | |
B | 出芽种子数 | 96 | 192 | 486 | 977 | 1946 |
发芽率 | 0.96 | 0.96 | 0.97 | 0.98 | 0.97 | |
下面有三个推断:①在同样的地质环境下播种,A种子的出芽率可能会高于B种子;②当实验种子数里为100时,两种种子的发芽率均为0.96所以它发芽的概率一样;③随着实验种子数量的增加,A种子出芽率在0.98附近摆动,显示出一定的稳定性,可以估计A种子出芽的概率是0.98.其中不合理的是 _____.(只填序号)
4、从3,0,,,这五个数中,随机抽取一个数作为m的值,则使函数的图象经过一、三象限,且使关于x的方程有实数根的概率是__________.
5、如图,在3×3正方形网格中,A、B在格点上,在网格的其它格点上任取一点C,能使△ABC为等腰三角形的概率是_____.
三、解答题(5小题,每小题10分,共计50分)
1、太原是国家历史文化名城,有很多旅游的好去处,周末哥哥计划带弟弟出去玩,放假前他收集了太原动物园、晋祠公园、森林公园、汾河湿地公园四个景点的旅游宣传卡片,这些卡片的大小、形状及背面完全相同,分别用D,J,S,F表示,如图所示,请用列表或画树状图的方法,求下列事件发生的概率.
(1)把这四张卡片背面朝上洗匀后,弟弟从中随机抽取一张,作好记录后,将卡片放回洗匀,哥哥再抽取一张,求两人抽到同一景点的概率;
(2)把这四张卡片背面朝上洗匀后,弟弟和哥哥从中各随机抽取一张(不放回),求两人抽到动物园和森林公园的概率.
2、某商家销售一批盲盒,每一个看上去无差别的盲盒内含有A,B,C,D四种玩具中的一种,抽到玩具B的有关统计量如表所示:
抽盲盒总数 | 500 | 1000 | 1500 | 2000 | 2500 | 3000 |
频数 | 130 | 273 | 414 | 566 | 695 | 843 |
频率 | 0.260 | 0.273 | 0.276 | 0.283 | 0.278 | 0.281 |
(1)估计从这批盲盒中任意抽取一个是玩具B的概率是 ;(结果保留小数点后两位)
(2)小明从分别装有A,B,C,D四种玩具的四个盲盒中随机抽取两个,请利用画树状图或列表的方法,求抽到的两个玩具恰为玩具A和玩具C的概率.
3、防疫期间,全市所有学校都严格落实测体温进校园的防控要求.某校开设了甲、乙、丙三个测温通道,某天早晨,该校小明和小丽两位同学将随机通过测温通道进入校园.
(1)小明从乙测温通道通过的概率是________;
(2)利用画树状图或列表的方法,求小明和小丽从同一个测温通道通过的概率.
4、甲、乙、丙、丁4人聚会,每人带了一件礼物,4件礼物外盒包装完全相同,将4件礼物放在一起.甲先从中随机抽取一件,不放回,乙再从中随机抽取一件,求甲、乙两人抽到的都不是自己带来的礼物的概率.
5、一个不透明的口袋中装有2个红球和1个白球,小球除颜色外其余均相同.
(1)从口袋中随机摸出一个小球,小球的颜色是白色的概率是 ;
(2)从口袋中随机摸出一个小球,记下颜色后放回,再随机摸出一个小球.请用画树状图(或列表)的方法,求两次摸出的小球颜色相同的概率.
-参考答案-
一、单选题
1、D
【分析】
必然事件是在一定条件下,一定会发生的事件;根据定义对选项进行判断,得出结果.
【详解】
解:A、B、C选项中的事件都是随机事件,不符合要求;
D选项中13人中至少有2人的出生月份相同是必然事件,符合要求;
故选D.
【点睛】
本题考查了必然事件.解题的关键在于正确理解必然事件与随机事件的定义.
2、A
【分析】
用红球的个数除以所有球的个数即可求得抽到红球的概率.
【详解】
解:∵共有5个球,其中红球有2个,
∴P(摸到红球)=,
故选:A.
【点睛】
此题主要考查概率的意义及求法.用到的知识点为:概率=所求情况数与总情况数之比.
3、B
【分析】
根据不可能事件的意义,结合具体的问题情境进行判断即可.
【详解】
解:A、射击运动员射击一次,命中靶心,是随机事件;故A不符合题意;
B、从一个只装有白球和红球的袋中摸球,摸出黄球,是不可能事件,故B符合题意;
C、班里的两名同学,他们的生日是同一天,是随机事件;故C不符合题意;
D、经过红绿灯路口,遇到绿灯,是随机事件,故D不符合题意;
故选:B.
【点睛】
本题考查随机事件,不可能事件,必然事件,理解随机事件,不可能事件,必然事件的意义是正确判断的前提.
4、B
【分析】
由在不透明的布袋中装有1个白球,2个红球,3个黑球,利用概率公式直接求解即可求得答案.
【详解】
解:∵在不透明的布袋中装有1个白球,2个红球,3个黑球,
∴从袋中任意摸出一个球,摸出的球是红球的概率是:.
故选:B.
【点睛】
此题考查了概率公式的应用.注意概率=所求情况数与总情况数之比.
5、B
【分析】
先画出树状图,再根据概率公式即可完成.
【详解】
所画树状图如下:
事件所有可能的结果数有6种,两次摸出的球都是白球的可能结果数有2种,则两次摸出的球都是白球的概率是:
故选:B
【点睛】
本题考查了利用树状图或列表法求概率,会用树状图或列表法找出所有事件的可能结果及某事件发生的可能结果是关键.
6、A
【分析】
设池中大概有鱼x尾,然后根据题意可列方程,进而问题可求解.
【详解】
解:设池中大概有鱼x尾,由题意得:,
解得:,
经检验:是原方程的解;
∴池塘主的做法有道理,池中大概有1200尾鱼;
故选A.
【点睛】
本题主要考查分式方程的应用及概率,熟练掌握分式方程的应用及概率是解题的关键.
7、D
【分析】
根据概率的意义去判断即可.
【详解】
∵“明天降雨的概率是80%”表示明天有降雨的可能性是80%,
∴A说法错误;
∵抛一枚硬币正面朝上的概率为”表示正面向上的可能性是,
∴B说法错误;
∵“彩票中奖的概率是1%”表示中奖的可能性是1%,
∴C说法错误;
∵“抛一枚均匀的正方体骰子,朝上的点数是2的概率为”表示随着抛掷次数的增加,“拋出朝上的点数是2”这一事件发生的概率稳定在附近,
∴D说法正确;
故选D.
【点睛】
本题考查了概率的意义,正确理解概率的意义是解题的关键.
8、D
【分析】
根据必然事件、不可能事件、随机事件的概念进行解答即可.
【详解】
解:“守株待兔”是随机事件.
故选D.
【点睛】
本题考查了必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.
9、D
【分析】
必然事件就是一定发生的事件,根据定义即可解答.
【详解】
解:A、小菊上学乘坐公共汽车是随机事件,不符合题意;
B、买10000张一定会中奖也是随机事件,尽管中奖率是1%,不符合题意;
C、一年中大月份有7个,小月份有5个,不相等,是不可能事件,不符合题意;
D、常温下油的密度<水的密度,所以油一定浮在水面上,是必然事件,符合题意.
故选:D.
【点睛】
用到的知识点为:必然事件指在一定条件下一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件.不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.
10、A
【分析】
根据概率公式计算即可.
【详解】
解:袋中装有3个红球和5个绿球共8个球,
从袋中随机摸出1个球是红球的概率为,
故选:A.
【点睛】
此题考查了概率的计算公式,正确掌握计算公式是解题的关键.
二、填空题
1、不合理 获得金牌是随机事件
【分析】
随机事件是指可能发生也可能不发生的事件,根据随机事件的定义进行解答即可.
【详解】
解:小健的说法不合理,因为获得金牌是随机事件,
故答案为:不合理,获得金牌是随机事件.
【点睛】
本题考查了随机事件的应用,能理解随机事件的定义是解此题的关键.
2、
【分析】
袋中有五个小球,3个红球,2个白球,利用概率公式直接求解即可求得答案.
【详解】
解:袋中有五个小球,3个红球,2个白球,形状材料均相同,
从中任意摸一个球,摸出红球的概率为,
故答案是:.
【点睛】
本题考查概率的求法,解题的关键是掌握如果一个事件有种可能,而且这些事件的可能性相同,其中事件出现种结果,那么事件的概率(A).
3、②
【分析】
根据随机事件发生的“频率”与“概率”的关系进行分析解答即可.
【详解】
①由表中数据可知,随着实验次数的增加,A种种子发芽的频率逐渐稳定在98%左右,而B种种子发芽的频率稳定在97%左右,故可以估计在相同条件下,A种种子发芽率大于B种种子发芽率,所以①中的说法是合理的.
②由表中的数据可知,当实验种子数量为100时,两种种子的发芽率虽然都是96%,但结合后续实验数据可知,此时的发芽率并不稳定,故不能确定两种种子发芽的概率就是96%,所以②中的说法不合理;
③由表中数据可知,随着实验次数的增加,A种种子发芽的频率逐渐稳定在98%左右,故可以估计A种种子发芽的概率是98%,所以③中的说法是合理的;
故答案为:②
【点睛】
本题考查了根据频率估计概率,理解“随机事件发生的频率与概率之间的关系”是正确解答本题的关键.
4、
【分析】
由正比例函数的图象及其性质可判断3,0,,,五个数均符合,由一元二次方程根的判别式可判断出只有,,三个数符合题意,故概率为.
【详解】
∵的图象经过一、三象限
∴
即
3,0,,,这五个数均符合
关于x的方程其中
则
令
解得时关于x的方程有实数根
故,,三个数符合题意
则P=.
故答案为:.
【点睛】
本题考查了正比例函数图象及其性质和一元二次方程根的判别式.当时正比例函数图象过第一、三象限,时正比例函数图象过第二、四象限;使用一元二次方程根的判别式,应先将方程整理成一般形式,再确定a,b,c的值.注意利用判别式可以判断方程的根的情况,反之,当方程有两个不相等的实数根时,;有两个相等的实数根时,;没有实数根时,.当时,方程有两个相等的实数根,不能说方程只有一个根.
5、
【分析】
分三种情况:①点A为顶点;②点B为顶点;③点C为顶点;得到能使△ABC为等腰三角形的点C的个数,再根据概率公式计算即可求解.
【详解】
如图,∵AB=,
∴①若AB=AC,符合要求的有3个点;
②若AB=BC,符合要求的有2个点;
③若AC=BC,不存在这样格点.
∴这样的C点有5个.
∴能使△ABC为等腰三角形的概率是.
故答案为:.
【点睛】
此题考查等腰三角形的判定和概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=.
三、解答题
1、(1);(2).
【分析】
(1)根据题意列表可得共有16种等可能的结果,其中两人抽到同一景点的结果有4种,进而由概率公式求解即可;
(2)根据题意列表可得共有12种等可能的结果,其中两人抽到动物园和森林公园的结果有2种,进而由概率公式求解即可.
【详解】
解:(1)列表如下:
| D | J | S | F |
D | (D,D) | (J,D) | (S,D) | (F,D) |
J | (D,J) | (J,J) | (S,J) | (F,J) |
S | (D,S) | (J,S) | (S,S) | (F,S) |
F | (D,F) | (J,F) | (S,F) | (F,F) |
所有等可能的情况数为16种,两人抽到同一景点的结果有4种,
所以两人抽到同一景点的概率为.
(2)列表如下:
| D | J | S | F |
D |
| (J,D) | (S,D) | (F,D) |
J | (D,J) |
| (S,J) | (F,J) |
S | (D,S) | (J,S) |
| (F,S) |
F | (D,F) | (J,F) | (S,F) |
|
所有等可能的情况数为12种,其中两人抽到动物园和森林公园的结果有2种,
所以两人抽到动物园和森林公园的概率为.
【点睛】
本题考查列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.
2、
(1)0.28;
(2)
【分析】
(1)由表中数据可判断频率在0.28左右摆动,利用频率估计概率可判断任意抽取一个毛绒玩具是优等品的概率为0.28;
(2)先列表得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解可得.
(1)
解:从这批盲盒中任意抽取一个是玩具B的概率是0.28,
故答案为0.28.
(2)
列表为:
| A | B | C | D |
A | -- | BA | CA | DA |
B | AB | -- | CB | DB |
C | AC | BC | -- | DC |
D | AD | BD | CD | -- |
由上表可知,从四种玩具的四个盲盒中随机抽取两个共有12种等可能结果,其中恰为玩具A和玩具C的结果有2种,所以恰为玩具A和玩具C的概率P=.
【点睛】
本题考查了利用频率估计概率及用列表法或树状图法求概率,大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.列表法或树状图法求概率,用到的知识点为:概率=所求情况数与总情况数之比.
3、(1);(2)
【分析】
(1)根据题意直接利用概率公式求解即可得出答案;
(2)由题意先列表得出所有等可能结果,从中找到符合条件的结果数,再利用概率公式进行计算可得.
【详解】
解:(1)小明从乙测温通道通过的概率是,
故答案为:;
(2)列表格如下:
| 甲 | 乙 | 丙 |
甲 | 甲,甲 | 乙,甲 | 丙,甲 |
乙 | 甲,乙 | 乙,乙 | 丙,乙 |
C | 甲,丙 | 乙,丙 | 丙,C |
由表可知,共有9种等可能的结果,其中小明和小丽从同一个测温通道通过的有3种可能,
所以小明和小丽从同一个测温通道通过的概率为=.
【点睛】
本题考查的是用列表法或画树状图法求概率.注意列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,用到的知识点为:概率=所求情况数与总情况数之比.
4、
【分析】
画出树状图,然后根据概率公式列式进行计算即可得解.
【详解】
解:设甲、乙、丙、丁4人的礼物分别记为a、b、c、d,
根据题意画出树状图如图:
一共有12种等可能的结果,甲、乙2人抽到的都不是自己带来的礼物的结果有7个,
∴甲、乙两人抽到的都不是自己带来的礼物的概率为.
【点睛】
本题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.
5、(1);(2)
【分析】
(1)根据概率公式计算即可;
(2)画出树状图即可得解;
【详解】
(1)根据题意可得,小球的颜色是白色的概率是;
故答案是:;
(2)根据题意画出树状图如下:
则两次摸出的小球颜色相同的概率为.
【点睛】
本题主要考查了概率公式的应用和画树状图求概率,准确画图计算是解题的关键.
初中数学第24章 圆综合与测试同步训练题: 这是一份初中数学第24章 圆综合与测试同步训练题,共26页。
初中沪科版第26章 概率初步综合与测试课后测评: 这是一份初中沪科版第26章 概率初步综合与测试课后测评,共19页。试卷主要包含了下列说法正确的是,有两个事件,事件,下列事件是必然发生的事件是等内容,欢迎下载使用。
沪科版九年级下册第26章 概率初步综合与测试一课一练: 这是一份沪科版九年级下册第26章 概率初步综合与测试一课一练,共20页。试卷主要包含了下列四幅图的质地大小,在一个不透明的布袋中,红色,一个不透明的口袋里有红,下列说法中正确的是等内容,欢迎下载使用。













