
2021-2022学年海南省海口市八年级(上)期末数学试卷 解析版
展开2021-2022学年海南省海口市八年级(上)期末数学试卷
一、选择题(每小题3分,共36分)在下列各题的四个备选答案中,只有一个是正确的,请把你认为正确的答案的字母代号填写在下表相应题号的方格内.
1.(3分)(﹣6)2的平方根是( )
A.﹣6 B.36 C.±6 D.±
2.(3分)下列说法中,正确的是( )
A.=±4 B.﹣32的算术平方根是3
C.1的立方根是±1 D.﹣是7的一个平方根
3.(3分)满足<x<的整数x的值是( )
A.3 B.4 C.2和3 D.3和4
4.(3分)下列计算正确的是( )
A.a2•a3=a6 B.3a2﹣a2=2
C.a8÷a2=a6 D.(﹣2a)3=﹣2a3
5.(3分)若(x+3)(x﹣5)=x2﹣mx﹣15,则m的值为( )
A.2 B.﹣2 C.5 D.﹣5
6.(3分)若x2﹣kx+16恰好是另一个整式的平方,则常数k的值为( )
A.±4 B.+4 C.±8 D.﹣8
7.(3分)若等腰三角形中有一个角等于40°,则这个等腰三角形顶角的度数为( )
A.40° B.100° C.40°或100° D.40°或70°
8.(3分)如图,在△ABC中,DE垂直平分AB,若AD=4,BC=3DC,则BC等于( )
A.4 B.4.5 C.5 D.6
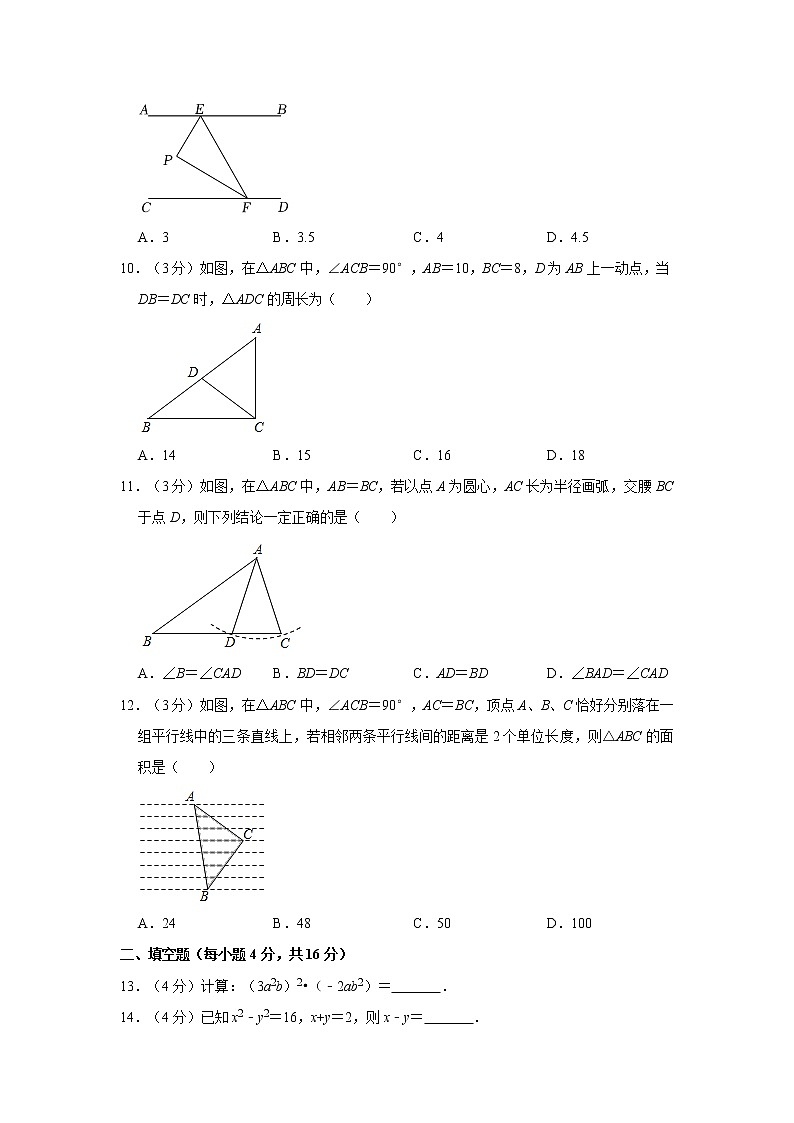
9.(3分)如图,直线AB∥CD,且这条两直线距离为8,∠AEF与∠EFC的角平分线交于点P,则点P到EF的距离为( )
A.3 B.3.5 C.4 D.4.5
10.(3分)如图,在△ABC中,∠ACB=90°,AB=10,BC=8,D为AB上一动点,当DB=DC时,△ADC的周长为( )
A.14 B.15 C.16 D.18
11.(3分)如图,在△ABC中,AB=BC,若以点A为圆心,AC长为半径画弧,交腰BC于点D,则下列结论一定正确的是( )
A.∠B=∠CAD B.BD=DC C.AD=BD D.∠BAD=∠CAD
12.(3分)如图,在△ABC中,∠ACB=90°,AC=BC,顶点A、B、C恰好分别落在一组平行线中的三条直线上,若相邻两条平行线间的距离是2个单位长度,则△ABC的面积是( )
A.24 B.48 C.50 D.100
二、填空题(每小题4分,共16分)
13.(4分)计算:(3a2b)2•(﹣2ab2)= .
14.(4分)已知x2﹣y2=16,x+y=2,则x﹣y= .
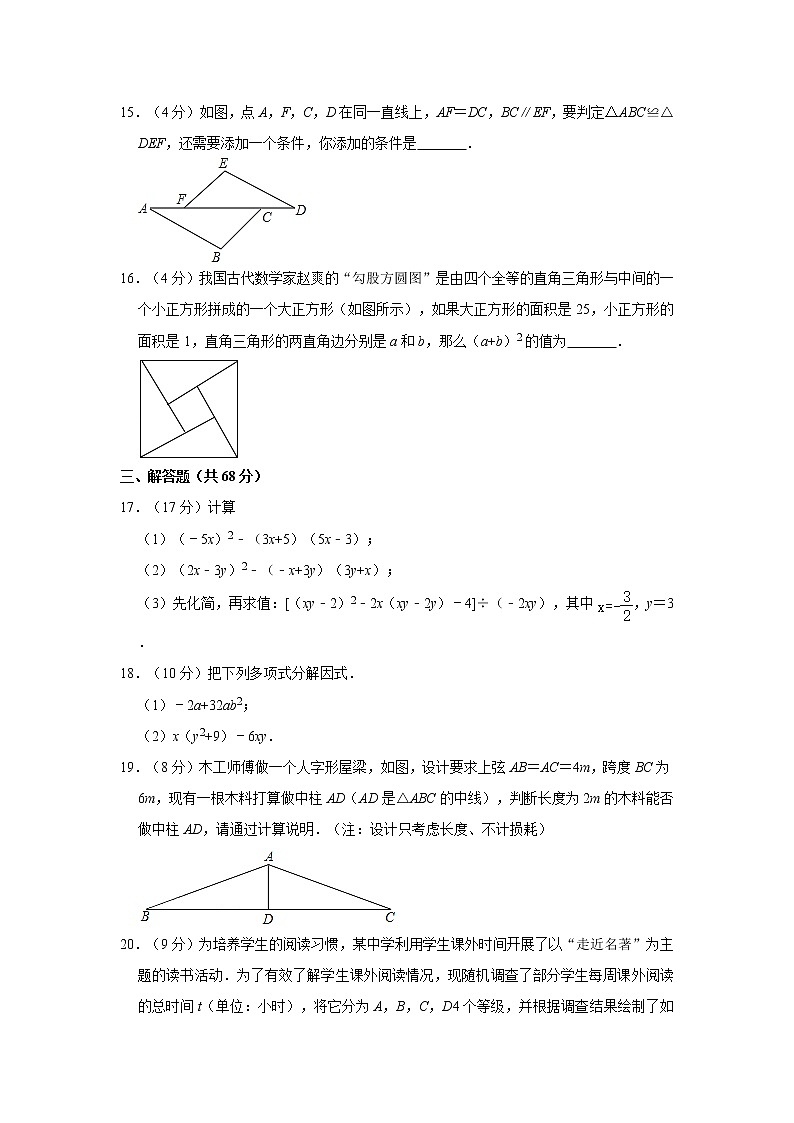
15.(4分)如图,点A,F,C,D在同一直线上,AF=DC,BC∥EF,要判定△ABC≌△DEF,还需要添加一个条件,你添加的条件是 .
16.(4分)我国古代数学家赵爽的“勾股方圆图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示),如果大正方形的面积是25,小正方形的面积是1,直角三角形的两直角边分别是a和b,那么(a+b)2的值为 .
三、解答题(共68分)
17.(17分)计算
(1)(﹣5x)2﹣(3x+5)(5x﹣3);
(2)(2x﹣3y)2﹣(﹣x+3y)(3y+x);
(3)先化简,再求值:[(xy﹣2)2﹣2x(xy﹣2y)﹣4]÷(﹣2xy),其中,y=3.
18.(10分)把下列多项式分解因式.
(1)﹣2a+32ab2;
(2)x(y2+9)﹣6xy.
19.(8分)木工师傅做一个人字形屋梁,如图,设计要求上弦AB=AC=4m,跨度BC为6m,现有一根木料打算做中柱AD(AD是△ABC的中线),判断长度为2m的木料能否做中柱AD,请通过计算说明.(注:设计只考虑长度、不计损耗)
20.(9分)为培养学生的阅读习惯,某中学利用学生课外时间开展了以“走近名著”为主题的读书活动.为了有效了解学生课外阅读情况,现随机调查了部分学生每周课外阅读的总时间t(单位:小时),将它分为A,B,C,D4个等级,并根据调查结果绘制了如图两幅不完整的统计图(图1,图2).
学生课外阅读总时间统计表
等级
时间/小时
A
0≤t<2
B
2≤t<4
C
4≤t<6
D
t≥6
请你根据以上统计图表提供的信息,解决下列问题:
(1)本次共调查了 名学生,请补全条形统计图;
(2)在扇形统计图中,等级D所对应的扇形的圆心角为 °;
(3)若该校有2000名学生,则每周课外阅读总时间不少于4小时的学生大约有 名.
21.(10分)如图,已知△ABC.
(1)利用直尺和圆规,根据下列要求作图(保留作图痕迹,不要求写作法).
①作∠ABC的平分线BD交AC于点D;
②作线段BD的垂直平分线交AB于点E,交BC于点F.
(2)在所作的图中,连接DE、DF.写出图中所有的等腰三角形: .
22.(14分)如图,在△ABC中,∠BAC=90°,AB=AC=3,D为BC边的中点,点E、F分别在AB、AC边上运动,且始终保持BE=AF,连接DE、DF、EF.
(1)求证:△ADE≌△CDF;
(2)判断△DEF的形状,并说明理由;
(3)求四边形AEDF的面积;
(4)若BE=2,求EF的长.
2021-2022学年海南省海口市八年级(上)期末数学试卷
参考答案与试题解析
一、选择题(每小题3分,共36分)在下列各题的四个备选答案中,只有一个是正确的,请把你认为正确的答案的字母代号填写在下表相应题号的方格内.
1.(3分)(﹣6)2的平方根是( )
A.﹣6 B.36 C.±6 D.±
【分析】首先根据平方的定义求出(﹣6)2的结果,然后利用平方根的定义即可解决问题.
【解答】解:∵(﹣6)2=36,
∴±=±6,
∴(﹣6)2的平方根是±6.
故选:C.
2.(3分)下列说法中,正确的是( )
A.=±4 B.﹣32的算术平方根是3
C.1的立方根是±1 D.﹣是7的一个平方根
【分析】根据立方根、平方根及算术平方根的定义逐项作出判断即可.
【解答】解:A、=4,故本选项错误;
B、﹣32=﹣9,根据负数没有平方根,故本选项错误;
C、1的立方根是1,故本选项错误;
D、﹣是7的一个立方根,故本选项正确.
故选:D.
3.(3分)满足<x<的整数x的值是( )
A.3 B.4 C.2和3 D.3和4
【分析】根据无理数的估计解答即可.
【解答】解:∵,
∴<x<的整数x的值是3和4,
故选:D.
4.(3分)下列计算正确的是( )
A.a2•a3=a6 B.3a2﹣a2=2
C.a8÷a2=a6 D.(﹣2a)3=﹣2a3
【分析】根据同底数幂的乘法,可判断A;根据合并同类项,可判断B;根据同底数幂的除法,可判断C;根据积的乘方,可判断D.
【解答】解:A、同底数幂的乘法底数不变指数相加,故A错误;
B、合并同类项系数相加字母部分不变,故B错误;
C、同底数幂的除法底数不变指数相减,故C正确;
D、积的乘方等于乘方的积,故D错误;
故选:C.
5.(3分)若(x+3)(x﹣5)=x2﹣mx﹣15,则m的值为( )
A.2 B.﹣2 C.5 D.﹣5
【分析】先把等式的左边化为x2﹣2x﹣15的形式,再求出m的值即可.
【解答】解:∵(x+3)(x﹣5)=x2﹣2x﹣15,
∴﹣m=﹣2,则m=2.
故选:A.
6.(3分)若x2﹣kx+16恰好是另一个整式的平方,则常数k的值为( )
A.±4 B.+4 C.±8 D.﹣8
【分析】利用完全平方公式的结构特征判断即可确定出k的值.
【解答】解:∵x2﹣kx+16恰好是另一个整式的平方,
∴k=±8,
故选:C.
7.(3分)若等腰三角形中有一个角等于40°,则这个等腰三角形顶角的度数为( )
A.40° B.100° C.40°或100° D.40°或70°
【分析】由等腰三角形中有一个角等于40°,可分别从①若40°为顶角与②若40°为底角去分析求解即可求得答案.
【解答】解:∵等腰三角形中有一个角等于40°,
∴①若40°为顶角,则这个等腰三角形的顶角的度数为40°;
②若40°为底角,则这个等腰三角形的顶角的度数为:180°﹣40°×2=100°.
∴这个等腰三角形的顶角的度数为:40°或100°.
故选:C.
8.(3分)如图,在△ABC中,DE垂直平分AB,若AD=4,BC=3DC,则BC等于( )
A.4 B.4.5 C.5 D.6
【分析】根据线段垂直平分线的性质即可得到结论.
【解答】解:∵DE垂直平分AB,若AD=4,
∴BD=AD=4,
∵BC=3DC,
∴BD=2CD,
∴CD=2,
∴BC=6,
故选:D.
9.(3分)如图,直线AB∥CD,且这条两直线距离为8,∠AEF与∠EFC的角平分线交于点P,则点P到EF的距离为( )
A.3 B.3.5 C.4 D.4.5
【分析】过P作PG⊥CD于G,交AB于H,作PM⊥EF于M,依据角平分线的性质,即可得到PH=PM=PG,再根据这条两直线距离为8,即可得到点P到EF的距离.
【解答】解:如图所示,过P作PG⊥CD于G,交AB于H,作PM⊥EF于M,
∵AB∥CD,
∴∠PHE=90°,
又∵∠AEF与∠EFC的角平分线交于点P,
∴PH=PM=PG,
∵这条两直线距离为8,
∴PH=PG=4,
∴PM=4,即点P到EF的距离为4,
故选:C.
10.(3分)如图,在△ABC中,∠ACB=90°,AB=10,BC=8,D为AB上一动点,当DB=DC时,△ADC的周长为( )
A.14 B.15 C.16 D.18
【分析】先根据勾股定理求出AC=6,再根据DB=DC时,△ADC的周长=AD+DC+AC=AB+AC求值即可.
【解答】解:∵∠ACB=90°,AB=10,BC=8,
∴AC===6,
当DB=DC时,
△ADC的周长=AD+DC+AC=AD+DB+AC=AB+AC=10+6=16.
故选:C.
11.(3分)如图,在△ABC中,AB=BC,若以点A为圆心,AC长为半径画弧,交腰BC于点D,则下列结论一定正确的是( )
A.∠B=∠CAD B.BD=DC C.AD=BD D.∠BAD=∠CAD
【分析】利用等腰三角形的性质分别判断后即可确定正确的选项.
【解答】解:∵AB=BC,
∴∠BAC=∠ACB,
∵以点A为圆心,AC长为半径画弧,交腰BC于点D,
∴AD=AC,
∴∠ACB=∠ADC,
∴∠ADC=∠BAC=∠ACB,
∴∠B=∠CAD,
故选:A.
12.(3分)如图,在△ABC中,∠ACB=90°,AC=BC,顶点A、B、C恰好分别落在一组平行线中的三条直线上,若相邻两条平行线间的距离是2个单位长度,则△ABC的面积是( )
A.24 B.48 C.50 D.100
【分析】过C作EF⊥该组平行线,交A所在直线于点E,交B所在直线于点F,易证∠CAE=∠BCF,即可证明△ACE≌△CBF,可得AE=CF,即可求得AC2的值,即可解题.
【解答】解:过C作EF⊥该组平行线,交A所在水平直线于点E,交B所在水平直线于点F,
∵∠ACE+∠BCF=90°,∠ACE+∠CAE=90°,
∴∠CAE=∠BCF,
在△ACE和△CBF中,
,
∴△ACE≌△CBF(AAS),
∴AE=CF=8,
∴AC2=AE2+CE2=100,
∴S△ABC=AC2=50,
故选:C.
二、填空题(每小题4分,共16分)
13.(4分)计算:(3a2b)2•(﹣2ab2)= ﹣18a5b4 .
【分析】直接利用积的乘方运算法则化简,再利用单项式乘单项式运算法则计算得出答案.
【解答】解:(3a2b)2•(﹣2ab2)
=9a4b2•(﹣2ab2)
=﹣18a5b4.
14.(4分)已知x2﹣y2=16,x+y=2,则x﹣y= 8 .
【分析】已知第一个等式左边利用平方差公式化简,将x+y=2代入计算即可求出x﹣y的值.
【解答】解:∵x2﹣y2=(x+y)(x﹣y)=16,x+y=2,
∴x﹣y=8,
故答案为:8
15.(4分)如图,点A,F,C,D在同一直线上,AF=DC,BC∥EF,要判定△ABC≌△DEF,还需要添加一个条件,你添加的条件是 EF=BC .
【分析】添加的条件:EF=BC,再根据AF=DC可得AC=FD,然后根据BC∥EF可得∠EFD=∠BCA,再根据SAS判定△ABC≌△DEF.
【解答】解:添加的条件:EF=BC,
∵BC∥EF,
∴∠EFD=∠BCA,
∵AF=DC,
∴AF+FC=CD+FC,
即AC=FD,
在△EFD和△BCA中,
∴△EFD≌△BCA(SAS).
故选:EF=BC.
16.(4分)我国古代数学家赵爽的“勾股方圆图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示),如果大正方形的面积是25,小正方形的面积是1,直角三角形的两直角边分别是a和b,那么(a+b)2的值为 49 .
【分析】根据正方形的面积公式以及勾股定理,结合图形进行分析发现:大正方形的面积即直角三角形斜边的平方25,也就是两条直角边的平方和是25,四个直角三角形的面积和是大正方形的面积减去小正方形的面积即2ab=24.根据完全平方公式即可求解.
【解答】解:由于大正方形的面积25,小正方形的面积是1,
则四个直角三角形的面积和是25﹣1=24,即4×ab=24,
即2ab=24,a2+b2=25,
则(a+b)2=a2+b2+2ab=25+24=49.
故答案为:49.
三、解答题(共68分)
17.(17分)计算
(1)(﹣5x)2﹣(3x+5)(5x﹣3);
(2)(2x﹣3y)2﹣(﹣x+3y)(3y+x);
(3)先化简,再求值:[(xy﹣2)2﹣2x(xy﹣2y)﹣4]÷(﹣2xy),其中,y=3.
【分析】(1)先算乘方和乘法,再去括号合并同类项即可得到答案;
(2)先用完全平方公式和平方差公式,再去括号合并同类项即可;
(3)先计算中括号内的完全平方及单项式乘多项式,再合并同类项,最后计算除法,化简后再将,y=3代入求值即可.
【解答】解:(1)原式=25x2﹣(15x2﹣9x+25x﹣15)
=25x2﹣15x2+9x﹣25x+15
=10x2﹣16x+15;
(2)原式=4x2﹣12xy+9y2﹣(9y2﹣x2)
=4x2﹣12xy+9y2﹣9y2+x2
=5x2﹣12xy;
(3)[(xy﹣2)2﹣2x(xy﹣2y)﹣4]÷(﹣2xy)
=(x2y2﹣4xy+4﹣2x2y+4xy﹣4)÷(﹣2xy)
=(x2y2﹣2x2y)÷(﹣2xy)
=﹣xy+x,
把,y=3代入得:
﹣xy+x
=﹣×(﹣)×3+(﹣)
=﹣
=.
18.(10分)把下列多项式分解因式.
(1)﹣2a+32ab2;
(2)x(y2+9)﹣6xy.
【分析】(1)直接提取公因式2a,再利用平方差公式分解因式,进而得出答案;
(2)直接提取公因式x,再利用完全平方公式分解因式得出答案.
【解答】解:(1)原式=2a(16b2﹣1)
=2a(4b+1)(4b﹣1);
(2)原式=x(y2﹣6y+9)
=x(y﹣3)2.
19.(8分)木工师傅做一个人字形屋梁,如图,设计要求上弦AB=AC=4m,跨度BC为6m,现有一根木料打算做中柱AD(AD是△ABC的中线),判断长度为2m的木料能否做中柱AD,请通过计算说明.(注:设计只考虑长度、不计损耗)
【分析】先根据等腰三角形的性质得出BD的长,在Rt△ABD中根据勾股定理求出AD的长即可.
【解答】解:∵AB=CD=4,AD是△ABC的中线,BC=6,
∴AD⊥BC,BD=BC=3.
由勾股定理,得AD===m.
∵2<,
∴长度为2m的木料不能做中柱AD.
20.(9分)为培养学生的阅读习惯,某中学利用学生课外时间开展了以“走近名著”为主题的读书活动.为了有效了解学生课外阅读情况,现随机调查了部分学生每周课外阅读的总时间t(单位:小时),将它分为A,B,C,D4个等级,并根据调查结果绘制了如图两幅不完整的统计图(图1,图2).
学生课外阅读总时间统计表
等级
时间/小时
A
0≤t<2
B
2≤t<4
C
4≤t<6
D
t≥6
请你根据以上统计图表提供的信息,解决下列问题:
(1)本次共调查了 50 名学生,请补全条形统计图;
(2)在扇形统计图中,等级D所对应的扇形的圆心角为 108 °;
(3)若该校有2000名学生,则每周课外阅读总时间不少于4小时的学生大约有 1320 名.
【分析】(1)由B等级人数及其所占百分比可得被调查的总人数;
(2)用360°乘以D等级人数所占的百分比得出等级D所对应的扇形的圆心角度数;用总人数减去其他等级的人数,求出C等级的人数,从而补全统计图;
(3)用总人数乘以不少于4小时的学生比例即可.
【解答】解:(1)本次共调查学生13÷26%=50(名);
故答案为:50;
(2)扇形统计图中,等级D所对应的扇形的圆心角为360°×=108°,
故答案为:108,
C等级人数为50﹣(4+13+15)=18(名),
补全图形如下:
(3)每周课外阅读总时间不少于4小时的学生大约有:2000×(1﹣26%﹣)=1320(人),
故答案为:1320.
21.(10分)如图,已知△ABC.
(1)利用直尺和圆规,根据下列要求作图(保留作图痕迹,不要求写作法).
①作∠ABC的平分线BD交AC于点D;
②作线段BD的垂直平分线交AB于点E,交BC于点F.
(2)在所作的图中,连接DE、DF.写出图中所有的等腰三角形: △BEF,△DEF,△EBD,△FBD .
【分析】(1)①利用尺规作出∠ABC的角平分线即可;
②利用尺规作出线段BD的垂直平分线即可;
(2)根据等腰三角形的定义判断即可.
【解答】解:(1)①如图2,射线BD就是所要求作的∠ABC的平分线;
②如图2,直线EF就是所要求作的线段BD的垂直平分线;
(2)∵EF垂直平分线段BD,
∴EB=ED,FB=FD,
∴△BED,△BFD是等腰三角形,
∵∠EBD=∠FBD,∠EBD+∠BEF=90°,∠FBD+∠BFE=90°,
∴∠BEF=∠BFE,
∴BE=BF=DE=DF,
∴△BEF,△DEF是等腰三角形.
故答案为:△BEF,△DEF,△EBD,△FBD.
22.(14分)如图,在△ABC中,∠BAC=90°,AB=AC=3,D为BC边的中点,点E、F分别在AB、AC边上运动,且始终保持BE=AF,连接DE、DF、EF.
(1)求证:△ADE≌△CDF;
(2)判断△DEF的形状,并说明理由;
(3)求四边形AEDF的面积;
(4)若BE=2,求EF的长.
【分析】(1)易证AD=DC,∠ADE=∠CDF,即可证明△ADE≌△CDF,即可解题;
(2)由(1)知,△ADE≌△CDF,得出DE=DF,∠ADE=∠CDF,即可得出结论;
(3)根据(1)中结论可得四边形AEDF的面积=S△ADC=S△ABC,即可解题;
(4)根据BE的长即可求得AE,AF的长,即可求得EF的长,即可解题.
【解答】(1)证明:∵∠BAC=90°,AB=AC,D为BC中点,
∴∠B=∠C=∠BAD=∠CAD=45°,∠ADC=90°,
∴AD=DC=BD,
∵∠ADE+∠ADF=90°,∠ADF+∠CDF=90°,
∴∠ADE=∠CDF,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(ASA);
(2)解:△DEF是等腰直角三角形,理由如下:
由(1)知,△ADE≌△CDF,
∴DE=DF,
∴∠ADE=∠CDF,
∴∠EDF=∠ADE+∠ADF=∠CDF+∠ADF=∠ADC=90°,
∴△DEF是等腰直角三角形;
(3)解:由(1)知,△ADE≌△CDF,
∴S△ADE=S△CDF,
∴四边形AEDF的面积=S△ADE+S△ADF=S△CDF+S△ADF=S△ADC=S△ABC,
∵S△ABC=AB•AC=,
∴四边形AEDF的面积=;
(4)解:∵AB=AC=3,BE=2,
∴AE=1,AF=BE=2,
∴EF==.
2021-2022学年海南省海口市八年级(上)期末数学试卷(B卷)(解析版): 这是一份2021-2022学年海南省海口市八年级(上)期末数学试卷(B卷)(解析版),共13页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2021-2022学年海南省海口市部分校八年级(下)期末数学试卷(Word解析版): 这是一份2021-2022学年海南省海口市部分校八年级(下)期末数学试卷(Word解析版),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2021-2022学年海南省海口市八年级(下)期末数学试卷(B卷)(Word解析版): 这是一份2021-2022学年海南省海口市八年级(下)期末数学试卷(B卷)(Word解析版),共15页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












