专题12.2 二次根式（提高篇）专项练习-【挑战满分】2021-2022学年八年级数学下册阶段性复习精选精练（苏科版）

这是一份专题12.2 二次根式（提高篇）专项练习-【挑战满分】2021-2022学年八年级数学下册阶段性复习精选精练（苏科版），共24页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
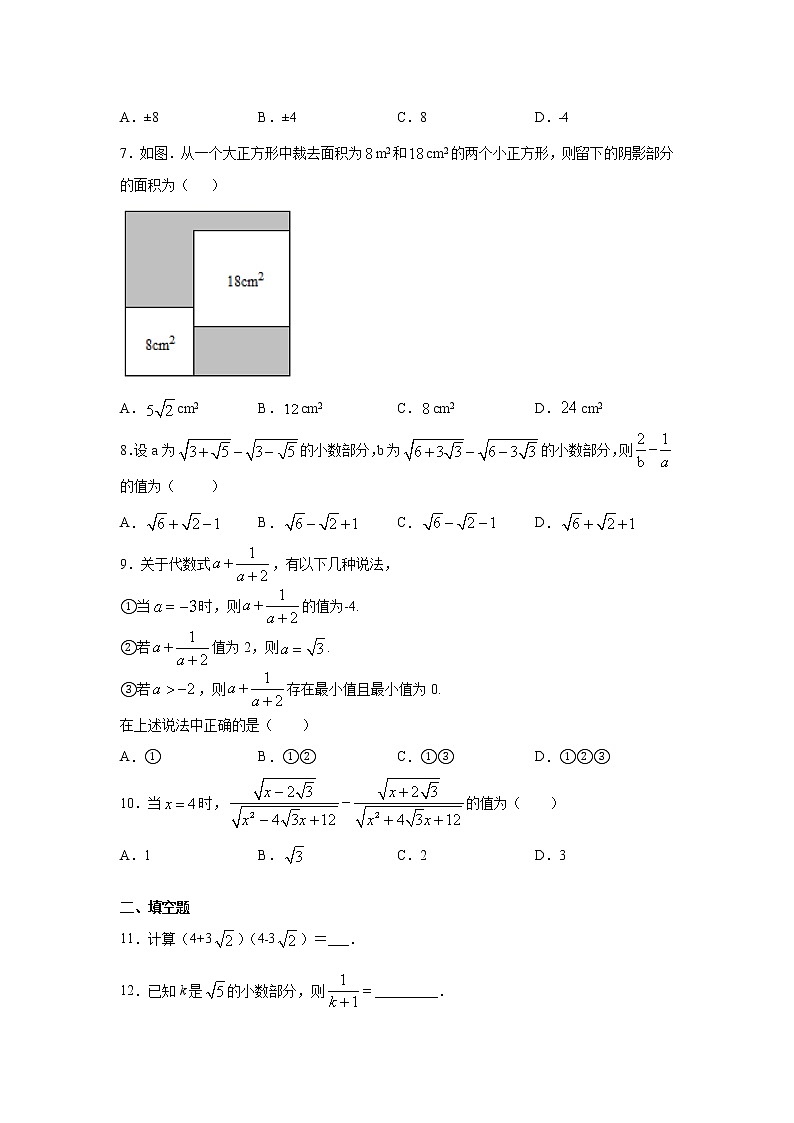
专题12.2   二次根式（提高篇）专项练习一、单选题1．下列二次根式中，是最简二次根式的是（    ）A． B． C． D．2．如果m是任意实数，那么下列代数式中一定有意义的是（　　）A． B． C． D．3．若a2+b2＝4ab，a>b>0，则＝（　　）A． B．3 C．﹣ D．﹣34．下列运算正确的是（    ）A．（﹣2a2b﹣1）2＝ B．（a＋b）2＝a2＋b2C．﹣3＝﹣2 D．＋＝5．《九章算术》中的“方田章”论述了三角形面积的求法：“圭田术曰，半广以乘正广”，就是说：“三角形的面积＝底×高÷2”，我国著名的数学家秦九韶在《数书九章》中也提出了“三斜求积术”，即可以利用三角形的三条边长来求取三角形面积，用现代式子可表示为：S＝（其中a、b、c为三角形的三条边长，S为三角形的面积）．如图，在平行四边形ABCD中，已知AB＝，AD＝，对角线BD＝，则平行四边形ABCD的面积为（    ）A． B． C． D．6．若二次根式有意义，且+（a﹣2）x+9是一个完全平方式，则满足条件的a值为（　　）A．±8 B．±4 C．8 D．﹣47．如图．从一个大正方形中裁去面积为m2和cm2的两个小正方形，则留下的阴影部分的面积为（   ）A．cm2 B．cm2 C．cm2 D．cm28．设a为的小数部分，b为的小数部分，则的值为（     ）A． B． C． D．9．关于代数式，有以下几种说法，①当时，则的值为-4.②若值为2，则.③若，则存在最小值且最小值为0.在上述说法中正确的是（　　）A．① B．①② C．①③ D．①②③10．当时，的值为（    ）A．1 B． C．2 D．3 二、填空题11．计算（4+3）（4﹣3）＝___．12．已知k是的小数部分，则_________．13．已知，则________．14．已知，，则的值是______．15．若，则_______．16．已知，那么可化简为_______________17．若实数满足，则的值是_________18．已知，则的值是_____．19．如果式子有意义，则的取值范围是：____________．20．我们定义为不超过a的最大整数．例如：．若，则a的取值范围是______________________．21．化简＝__．22．若，，是实数，且，则________．23．，，，，，其中n为正整数，则的值是__________． 三、解答题24．计算：（1）；                    （2）；  （3）；            （4）．  25．先化简再求值：（）•，其中a＝2+，b＝2﹣．  26．（1）由8个同样大小的立方体组成的魔方，体积为64，则出这个魔方的棱长是_______．（2）图1正方形的边长等于魔方的棱长，求出阴影部分的面积及其边长．（3）把正方形放到数轴上，如图2，使得A与重合，那么D在数轴上表示的数为______．   27．若三个实数x，y，z满足xyz≠0，且x+y+z＝0，则有：＝|++|．例如：＝＝|++|＝请解决下列问题：（1）求的值．（2）设S＝++…+，求S的整数部分．（3）已知x+y+z＝0（xyz≠0，x＞0），且y+z＝3yz，当+|﹣﹣|取得最小值时，求x的取值范围．   28．（阅读材料）小慧同学数学写作片段乘法公式“大家族”学习《整式的乘法及因式分解》之后，我发现乘法公式不只是教材上“黑体字”明确的“平方差公式”“完全平方公式和”，其实在教材或平时的练习中还“隐含”一些“乘法公式”值得积累，比如，；；；．……（解题运用）（1）在实数范围内因式分解：___________；（2）设满足等式，求的值；（3）若正数满足等式，求代数式的值．
参考答案1．B【分析】最简二次根式的概念：被开方数不含分母，被开方数中不含能开得尽方的因数或因式，这样的二次根式，叫做最简二次根式．【详解】解：A. 被开方数含有开得尽的因数不是最简二次根式，不符合题意；B. 是最简二次根式，符合题意；C. 被开方数含有分母，不是最简二次根式，不符合题意；D. 被开方数含有开得尽的因数不是最简二次根式，不符合题意．故选：B．【点拨】本题考查最简二次根式的概念，解题的关键是能够看出被开方数中的能开得尽方的因数或因式．2．D【分析】根据二次根式有意义，二次根式中的被开方数是非负数，分式有意义，分母不为零,进行分析即可．【详解】解：A、当m＜0时，无意义，故此选项不符合题意；B、当m＜﹣1时，无意义，故此选项不符合题意；C、当m＝﹣1时，无意义，故此选项不符合题意；D、m是任意实数，都有意义，故此选项符合题意；故选：D．【点拨】本题考查了二次根式有意义的条件，分式有意义的条件，熟练掌握二式有意义的基本条件是解题的关键．3．C【分析】由a2+b2＝4ab可得，，再由a>b>0，可得b -a<0，a+b>0，根据二次根式的性质可得b –a= ，a+b=，整体代入后化简即可求解．【详解】∵a2+b2＝4ab，∴，，∵a＞b＞0，∴b -a<0，a+b>0，ab>0，∴b –a= ，a+b=，∴＝．故选C．【点拨】本题考查了完全平方公式的变形及二次根式的性质，正确求得b –a= 及a+b=是解决问题的关键．4．A【分析】直接利用积的乘方运算法则以及完全平方公式、二次根式的加减、分式的加减运算法则分别计算得出答案．【详解】解：A、（﹣2a2b﹣1）2＝，故此选项正确；B、（a+b）2＝a2+2ab+b2，故此选项错误；C、﹣3＝﹣2，故此选项错误；D、＝﹣＝，故此选项错误；故选：A．【点拨】此题主要考查了积的乘方运算以及完全平方公式、二次根式的加减、分式的加减运算，正确掌握相关运算法则是解题关键．5．B【分析】根据已知条件的公式计算即可；【详解】根据题意可知：a＝，b＝，c＝，∴S＝，＝，，，，∴，∴；故答案选B．【点拨】本题主要考查了二次根式的应用，准确分析计算是解题的关键．6．D【分析】根据二次根式有意义的条件列出不等式，解不等式求出a的范围，根据完全平方式求出a，根据题意判断，得到答案．【详解】解：∵二次根式有意义，∴6﹣2a≥0，解得，a≤3，∵+（a﹣2）x+9是一个完全平方式，∴a﹣2＝±6，解得，a＝8，或a＝﹣4，∵a≤3，∴a＝﹣4，故选：D．【点拨】本题考查了二次根式有意义的条件，完全平方公式，熟练掌握有意义的条件，准确理解完全平方式的意义是解题的关键．7．D【分析】直接利用正方形的性质得出两个小正方形的边长，进而得出大正方形的边长，即可得出答案．【详解】解：∵两个小正方形面积为8cm2和18cm2，∴大正方形边长为：，∴大正方形面积为（5）2=50，∴留下的阴影部分面积和为：50-8-18=24（cm2）故选：D．【点拨】此题主要考查了二次根式的应用，正确得出大正方形的边长是解题关键．8．B【分析】首先分别化简所给的两个二次根式，分别求出a、b对应的小数部分，然后化简、运算、求值，即可解决问题．【详解】∴a的小数部分为，∴b的小数部分为，∴，故选：B．【点拨】该题主要考查了二次根式的化简与求值问题；解题的关键是灵活运用二次根式的运算法则来分析、判断、解答．9．C【分析】①将代入计算验证即可；②根据题意=2，解得a的值即可作出判断；③若a＞-2，则a+2＞0，则对配方，利用偶次方的非负性可得答案．【详解】解：①当时，
．
故①正确；
②若值为2，
则，
∴a2+2a+1=2a+4，
∴a2=3，
∴．
故②错误；
③若a＞-2，则a+2＞0，
∴===≥0．
∴若a＞-2，则存在最小值且最小值为0．
故③正确．
综上，正确的有①③．
故选：C．【点拨】本题考查了分式的加减法、分式的值的计算及最值问题等知识点，熟练运用相关公式及运算法则是解题的关键．10．A【分析】根据分式的运算法则以及二次根式的性质即可求出答案．【详解】解：原式=将代入得，原式.故选：A.【点拨】本题考查分式的运算以及二次根式的性质，解题的关键是熟练运用分式的运算法则以及观察出分母可以开根号，本题属于较难题型．11．-2【分析】根据平方差公式进行计算即可得到答案．【详解】解：故答案为：-2．【点拨】本题考查了二次根式的混合运算和平方差公式，解题的关键是掌握二次根式的运算法则和平方差公式的运用．12．【分析】先估算出k的值，再代入化简即可．【详解】解：∵ ∴ ∴故答案为：【点拨】本题考查无理数的估算、二次根式的化简，掌握二次根式的运算法则是得出正确答案的前提．13．2【分析】根据二次根式有意义的条件得到关于x的不等式组，求出x，代入求出y，即可求解．【详解】解：由题意得： ，解得x＝ ∴＝－1∴故答案为2．【点拨】本题考查了二次根式有意义的条件，负整数指数幂等知识，根据二次根式有意义的条件求出x、y的值是解题关键．14．100【分析】先计算，即可得到的值．【详解】∵，∴∴=故答案为：100．【点拨】此题主要考查二次根式的运算，解题的关键是熟知其运算法则．15．．【分析】根据根据二次根式的被开方数是非负数知，易得，代入求值即可．【详解】解：∵，，∴，，∴，∴，∴故答案是：．【点拨】考查了二次根式的意义和性质，熟悉相关性质是解题的关键．16．【分析】由，可得＜，再化简即可得到答案．【详解】解： ，, ， 原式＝．故答案为：【点拨】本题考查的是二次根式的化简，掌握利用二次根式的性质化简二次根式是解题的关键．17．【分析】把已知条件化为两个完全平方式，可知两个非负数相加为0，则每个式子都为0，从而列方程求出x和y，代入即可解答．【详解】解：∵∴∴∴∴．故答案为：．【点拨】本题主要考查了非负数的性质以及二次根式的混合运算，两非负数之和等于0，则两数均为0，求得x、y值．本题中把变形得是解题的关键．18．31【分析】先对x，y分母有理化，再代入求值，即可．【详解】∵，∴====31，故答案是：31．【点拨】本题主要考查二次根式的混合运算，熟练掌握二次根式的分母有理化，是解题的关键．19．且【分析】根据分式有意义可得，根据二次根式有意义的条件可得，求解即可．【详解】解：由题意得：，且，解得：且，故答案为：且．【点拨】本题主要考查了分式有意义和二次根式有意义的条件，关键是掌握分式有意义的条件是分母不等于零，二次根式中的被开方数是非负数．20．【分析】结合定义内容及二次根式成立的条件确定a的取值范围．【详解】解：由题意可得，解得故答案为：．【点拨】本题考查二次根式的大小比较及二次根式成立的条件，准确理解题意，列出不等式组正确计算是解题关键．21．【分析】先利用完全平方公式得到4﹣2＝（﹣1）2，则原式可化为简为，再利用2+＝，则原式可化简为，然后就计算二次根式的除法运算．【详解】解：∵4﹣2＝（﹣1）2，∴＝，∵2+＝＝，∴原式＝＝＝．故答案为．【知识点】本题考查了分母有理化、二次根式的混合运算，适当的把有关式子变成完全平方的形式是解题关键．22．21【分析】结合态，根据完全平方公式的性质，将代数式变形，即可计算得，，的值，从而得到答案．【详解】∵∴∴∴∴∴∴∴．【点拨】本题考查了二次根式、完全平方公式的知识；解题的关键是熟练掌握二次根式、完全平方公式、一元一次方程的性质，从而完成求解．23．【分析】根据题目条件，先求出，，，的值，代入原式后求出各式的算术平方根，再利用裂项公式进行化简与计算，即可求解．【详解】解：，，，    ，，，，，，．故答案为．【点拨】本题考查了二次根式的化简求值，解题的关键是找出，，，的值的规律，再用裂项法求出结果．24．（1）；（2）；（3）；（4）【分析】（1）直接利用二次根式的乘法运算法则计算得出答案；（2）直接化简二次根式进而计算得出答案；（3）直接利用二次根式的混合运算法则计算得出答案；（4）直接利用二次根式的混合运算法则计算得出答案．【详解】解：（1）；（2）；（3）；（4）．【点拨】此题主要考查了二次根式的混合运算，正确掌握相关运算法则是解题关键．25．【分析】根据分式的减法和乘法可以化简题目中的式子，然后将a、b的值代入化简后的式子即可解答本题．【详解】解：（）•，＝[]•，＝（）•，＝，＝，当a＝2+，b＝2﹣时，原式＝＝＝＝．【点拨】本题考查了分式的化简求值和二次根式的运算，解题关键是熟练运用分式的运算法则和二次根式运算法则进行计算．26．（1）4；（2）阴影部分的面积是8，边长是；（3）-1-【分析】（1）根据正方体的体积公式可求这个魔方的棱长．（2）根据魔方的棱长为4，所以小立方体的棱长为2，阴影部分由4个直角三角形组成，算出一个直角三角形的面积乘以4即可得到阴影部分的面积，开平方即可求出边长．（3）根据两点间的距离公式可得D在数轴上表示的数．【详解】解：（1）=4，答：这个魔方的棱长为4．（2）∵魔方的棱长为4，∴小立方体的棱长为2，∴阴影部分面积为：×2×2×4=8，边长为：=；答：阴影部分的面积是8，边长是；（3）D在数轴上表示的数为-1-，故答案为：-1-．【点拨】本题考查的是立方根在实际生活中的运用，解答此题的关键是根据立方根求出魔方的棱长．27．（1）；（2）2019；（3）0＜x≤【分析】（1）根据范例中提供的计算方法进行计算即可；（2）将原式进行化简，再确定整数部分；（3）将原式化简为||+||，再根据||+||取最小值时，确定x的取值范围．【详解】解：（1）＝＝|++|＝；（2）S＝++…+，＝++…+，＝|1+1﹣|+|1+﹣|+…+|1+﹣|，＝1+1﹣+1+﹣+1+﹣+…+1+﹣，＝2019+，故整数部分为2019；（3）由题意得，+|﹣﹣|，＝|++|+|﹣﹣|，＝||+||，又y+z＝3yz，原式＝||+||，因为||+||取最小值，所以﹣3≤≤3，而x＞0，因此，0＜x≤，答：x的取值范围为0＜x≤．【点拨】本题考查了分式的加减法、实数的运算、二次根式的运算，解题关键是掌握数字间的变化规律，准确计算．28．（1）；（2）12；（3）．【分析】（1）根据公式即可完成多项式的因式分解；（2）利用公式法将多项式转化为，求得即可计算出结果；（3）利用公式可将分解为，并再根据完全平方公式将分解结果转化为，再由已知可推出，将其代入化简后的代数式即可得出计算结果．【详解】解：（1），故答案为：．（2），则，∴∴．（3）．∵，∴，∴，∴原式．【点拨】本题主要考查了因式分解的应用，掌握因式分解的基本方法，牢记因式分解的相关公式且准确灵活运用公式是解题的关键．