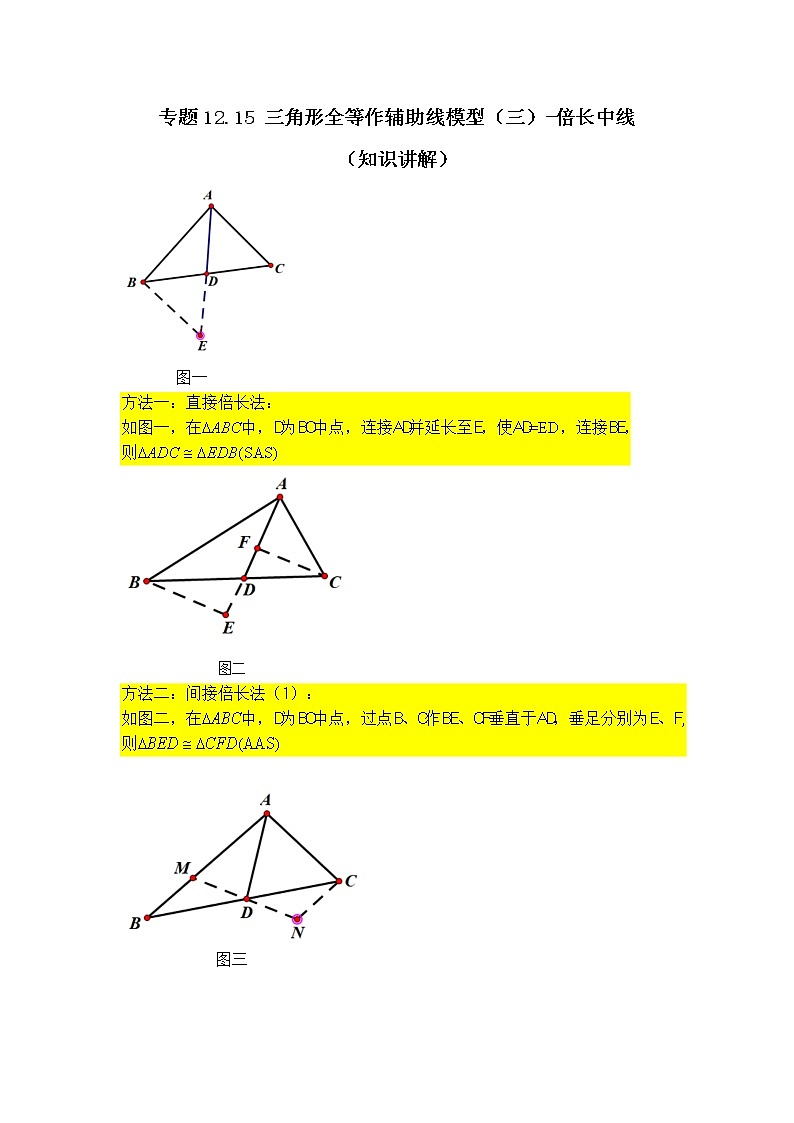
专题12.15 三角形全等作辅助线模型（三）-倍长中线（知识讲解）-2021-2022学年八年级数学上册基础知识专项讲练（人教版）

专题12.15 三角形全等作辅助线模型（三）-倍长中线

（知识讲解）

       图一

图二

图三

【典型例题】

1、（2020·江西南昌市·）如图所示，在中，为中线，，求的度数．

【答案】45°

【分析】

延长AD至E，使，连结，则，根据全等三角形的性质得EC=AB，，由AB=2AD可得EC=AE，可得△AEC是等腰直角三角形，即可得∠DAC的度数．

解：延长AD至E，使，连结，

∵BD=CD，∠ADB=∠EDC

∴，

∴EC=AB，，

∵AB=2AD，

∴AB=AE=EC

∴△AEC是等腰直角三角形，

∴∠DAC=45°.

故答案为45°.

【点拨】本题考查全等三角形的判定与性质, 等腰直角三角形的性质，解题的关键是作辅助线构建全等三角形和等腰直角三角形.

举一反三：

【变式】如图所示，为的角平分线，分别在上，，若．

求证：．

【答案】详见解析

【分析】延长FD至G，使，连结CG，可证，则EF=CG，利用全等三角形和角平分线以及平行线的性质可得 ，根据等角对等边得AC=CG，即可得出结论.

证明：延长FD至G，使，连结CG，

∵DC=DE，∠EDF=∠CDG，

∴，

，

，

，

又，

，

，

.

【点拨】本题考查全等三角形的判定和性质，关键是证△EDF 与△CDG 全等．

2、 阅读理解：

（1）如图1，在中，若，，求边上的中线的取值范围．解决此问题可以用如下方法：延长到点，使得，再连接，把，，集中在中，利用三角形三边关系即可判断中线的取值范围是______．

（2）解决问题：如图2，在中，是边上的中点，，交于点，交于点，连接，求证：．

（3）问题拓展：如图3，在中，是边上的中点，延长至，使得，求证：．

【答案】（1）；（2）见解析；（3）见解析．

【分析】

（1）如图1延长到点，使得，再连接，由AD为中线，推出BD=CD，可证△ACD≌△EBD（SAS）得AC=EB，在中，由三边关系即可，

（2）如图2延长FD到G，使DG=FD，连结BG，EG由D为BC中点，BD=CD可证△FCD≌△GBD（SAS）得FC=GB，由，DF=DG得EF=EG，在△BEG中 由三边关系，

（3）如图3，延长AD到G使DG=AD，连结BG，由是边上的中点，得BD=CD，可证△ACD≌△GBD（SAS）得AC=GB，∠DAC=∠G，利用BE=BG即可推得答案，

解答：（1）如图1延长到点，使得，再连接，

∵AD为中线，

∴BD=CD，

在△ADC和△ EDB中，

∵CD=BD，

∠ADC=∠EDB，

AD=ED，

∴△ACD≌△EBD（SAS），

∴AC=EB=6，

，

∵，

∴，

∴，

（2）如图2延长FD到G，使DG=FD，连结BG，EG，

由D为BC中点，BD=CD，

在△FDC和△GDB中，

∵CD=BD，

∠FDC=∠GDB，

FD=GD，

∴△FCD≌△GBD（SAS），

∴FC=GB，

∵，DF=DG，

∴EF=EG，

在△BEG中EG<EB+BG，即，

（3）如图3，延长AD到G使DG=AD，连结BG，

由是边上的中点，

∴BD=CD，

在△ADC和△GDB中，

∵CD=BD，

∠ADC=∠GDB，

AD=GD，

∴△ACD≌△GBD（SAS），

∴AC=GB，∠DAC=∠G，

∵BE=AC，

∴BE=BG，

∴∠BED=∠G=∠CAD．

【点拨】本题考查中线加倍，三角形全等，三边关系，垂直平分线，等腰三角形，掌握中线加倍构造三角形，用三角形全等转化等量关系，用三边关系求取值范围，用垂直平分线转化线段，用等腰三角形证角是解题关键，

举一反三：

【变式】  如图，在ABC中，AC=2AB，AD平分∠BAC，延长CB到点E，使BE=BD，连接AE．

（1）依题意补全图形；

（2）试判断AE与CD的数量关系，并进行证明．

【分析】

（1）直接延长CB到点E，使BE=BD即可；

（2）延长至点，使得，连接，可证得，则，再通过证明，可得到，从而得到即可．

解答：（1）如图所示：

（2）如图，

判断：

证明如下：

延长至点，使得，连接

在和中，

∵

∴

∴

∵

∴

∵

∴

∵AD平分∠BAC

∴

在和中，

∵

∴

∴

又∵

∴

【点拨】本题考查全等三角形的判定与性质，主要涉及倍长中线的模型，熟记基本模型是解题关键．

3、如图，已知，点是的中点，且，求证：．

 【分析】延长AE、BC交于点M，利用AAS证出△ADE≌△MCE，从而得出AD=MC，AE=ME，结合已知条件即可证出BM=AB，再利用SSS即可证出△BAE≌△BME，从而得出∠BEA=∠BEM，根据垂直定义即可证出结论．

证明：延长AE、BC交于点M，如下图所示

∵点是的中点，

∴DE=CE，

∵

∴∠1=∠M

在△ADE和△MCE中

∴△ADE≌△MCE

∴AD=MC，AE=ME

∵

∴MC＋BC=AB

∴BM=AB

在△BAE和△BME中

∴△BAE≌△BME

∴∠BEA=∠BEM

∵∠BEA＋∠BEM=180°

∴∠BEA=∠BEM=90°

∴

【点拨】此题考的是全等三角形的判定及性质、平行线的性质和垂直的定义，掌握全等三角形的判定及性质、平行线的性质和垂直的定义是解题关键．

举一反三：

【变式1】 （2020·河北邢台市·金华中学八年级期中）某数学兴趣小组在一次活动中进行了探究试验活动，请你来加入．

（探究与发现）

（1）如图1，AD是的中线，延长AD至点E，使，连接BE，证明：．

（理解与应用）

（2）如图2，EP是的中线，若，，设，则x的取值范围是________．

（3）如图3，AD是的中线，E、F分别在AB、AC上，且，求证：．

【答案】（1）见解析；（2）；（3）见解析

【分析】

（1）根据全等三角形的判定即可得到结论；

（2）延长至点，使，连接，根据全等三角形的性质得到，根据三角形的三边关系即可得到结论；

（3）延长FD至G，使得，连接BG，EG，结合前面的做题思路，利用三角形三边关系判断即可．

（1）证明：，，，

，

（2）；

如图，延长至点，使，连接，

在与中，

，

，

，

在中，，

即，

的取值范围是；

故答案为：；

（3）延长FD至G，使得，连接BG，EG，

在和中，，，，

，，

在和中，

，，，

，，

在中，两边之和大于第三边

，，

又，，

【点拨】本题考查了全等三角形的判定和性质，三角形的中线的定义，三角形的三边关系，正确的作出图形是解题的关键．

举一反三：

【变式2】 如图，AB=AE，AB⊥AE，AD=AC，DE=2AM，点M为BC的中点，连接AM．求证：AD⊥AC

 【分析】延长AM至N，使MN=AM，证△AMC≌△NMB，推出AC=BN=AD，ED=AN，证△EAD≌△ABN，得到∠EAD+∠BAC=180°，即可证明AD⊥AC．

证明：延长AM至N，使MN=AM，连接BN，

∵点M为BC的中点，
∴CM=BM，
在△AMC和△NMB中，

，

∴△AMC≌△NMB（SAS），
∴AC=BN，∠C=∠NBM，∠CAM=∠N，

∵DE=2AM，AD=AC，

∴DE= AN，AD= BN，

在△EAD和△ABN中，

，

∴△EAD≌△ABN（SSS），

∴∠EAD=∠ABN，

∴∠EAD+∠BAC=∠EAD+∠BAN+∠CAM=∠ABN+∠BAN+∠N=180，

∵AB⊥AE，

∴∠EAB=90°，

∴∠DAC=360°-∠EAB-(∠EAD+∠BAC)= 90°，

∴AD⊥AC．

【点拨】本题考查了三角形内角和定理的应用，全等三角形的性质和判定的应用，主要考查学生的推理能力，延长AM至N，使MN=AM，利用“中线倍长”构造全等三角形的是解题的关键．