2021年江西省重点中学盟校高考数学第一次联考试卷（文科）

这是一份2021年江西省重点中学盟校高考数学第一次联考试卷（文科），共8页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。


1. 已知集合U＝{1, 2, 3, 4, 5, 6}，M＝{2, 3, 4}，N＝{4, 5, 6}，则(∁UM)∩N＝（ ）
A.{6}B.{4, 6}C.⌀D.{5, 6}

2. 已知i是虚数单位，则复数的虚部是（ ）
A.−1B.1C.−iD.i

3. 已知||＝2，||＝1，且＝−1，则＝（ ）
A.6B.8C.3D.−3

4. 甲乙俩人投篮相互独立，且各投篮一次命中的概率分别是0.4和0.3，则甲乙俩人各投篮一次，至少有一人命中的概率为（ ）
A.0.7

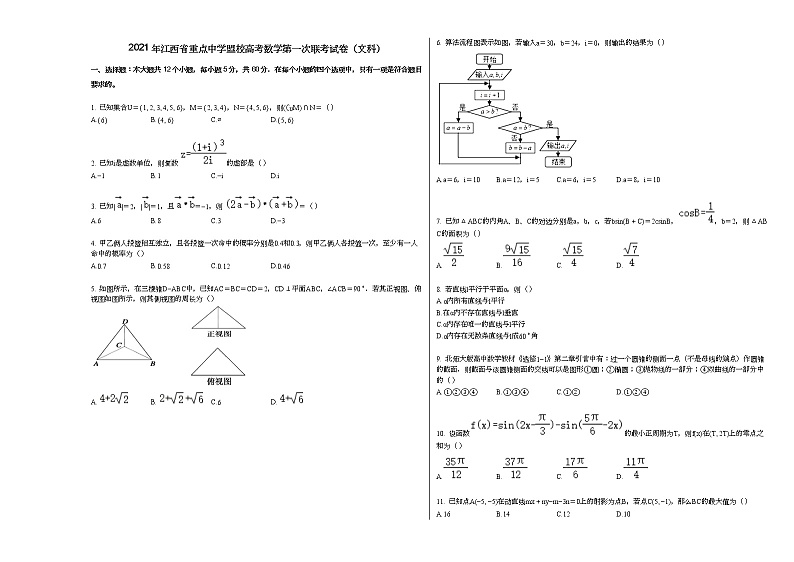
5. 如图所示，在三棱锥D−ABC中，已知AC＝BC＝CD＝2，CD⊥平面ABC，∠ACB＝90∘．若其正视图、俯视图如图所示，则其侧视图的周长为（ ）

A.B.C.6D.

6. 算法流程图表示如图，若输入a＝30，b＝24，i＝0，则输出的结果为（ ）

A.a＝6，i＝10B.a＝12，i＝5C.a＝6，i＝5D.a＝8，i＝10

7. 已知△ABC的内角A、B、C的对边分别是a，b，c，若bsin(B+C)＝2csinB，，b＝2，则△ABC的面积为（ ）
A.B.C.D.

8. 若直线l平行于平面α，则（ ）
A.α内所有直线与l平行
B.在α内不存在直线与l垂直
C.α内存在唯一的直线与l平行
D.α内存在无数条直线与l成60∘角

9. 北师大版高中数学教材《选修1−1》第二章引言中有：过一个圆锥的侧面一点（不是母线的端点）作圆锥的截面．则截面与该圆锥侧面的交线可以是图形①圆；②椭圆；③抛物线的一部分；④双曲线的一部分中的（ ）
A.①②③④B.①③④C.①②D.①②④

10. 设函数的最小正周期为T，则f(x)在(T, 2T)上的零点之和为（ ）
A.B.C.D.

11. 已知点A(−5, −5)在动直线mx+ny−m−3n＝0上的射影为点B，若点C(5, −1)，那么BC的最大值为（ ）
A.16B.14C.12D.10

12. 已知定义在R上的函数f(x)的导函数为f′(x)，且f′(x)−f(x)>1恒成立，e为自然常数．则下列选项中正确的是（ ）
A.f(1)−e2f(−1)C.ef(0)−f(1)<1−eD.f(2020)>f(2019)
二、填空题：本题共4小题，每小题5分，共20分。

若变量x，y满足，则2x+y的最小值为________．

定义在R上的函数f(x)满足f(x)+f(−x)＝0．当x≥0时，f(x)＝x2−x+a−1，则f(−3)＝________．

将连续正偶数有规律地排列如下：
则在此表中第15行第14列出现的数字是________．

已知抛物线C:x2＝8y，焦点为F，过F的直线l交C于A，B两点，分别作抛物线C在A，B处的切线，且两切线交于点P，则点P的轨迹方程为________．
三．解答题：共70分，解答应写出文字说明、证明过程或演算步骤，第17-21题为必考题，每个试题考生都必须作答；第22、23题为选考题，考生根据要求作答。（一）必考题：共60分。

已知数列{an}的前n项和为Sn，n∈N*且．
(Ⅰ)求数列{an}的通项公式；
(Ⅱ)若，求数列{bn}的前n项和Tn．

如图，在四棱锥P−ABCD中，四边形ABCD为直角梯形，AD // BC，∠ADC＝90∘，平面PAD⊥平面ABCD，Q、M分别为AD、PC的中点，PD＝AD＝4，PQ＝2CD＝2，BC＝2．

（1）求证：AD⊥PB；

（2）求三棱锥P−QMB的体积．

为了比较两种治疗新冠病毒的临床试验阶段药（分别称为甲药，乙药）的疗效，某医疗团队随机地选取了服用甲药的患者和服用乙药的患者进行研究，从服用甲药的治愈患者和服用乙药的治愈患者中，分别抽取了10名，记录他们的治疗时间（单位：天），统计并绘制了茎叶图：

（1）医院从这10名服用乙药的治疗时间为10天到30天之间的治愈患者中随机的抽取2名患者回访，求恰好抽到一名治愈患者治疗时间超过20天的概率；

（2）标准差s除了可以用来刻画一组数据的离散程度外，还可以刻画每个数据偏离平均水平的程度，如果出现了治疗时间在（+3s)之外的患者，就认为该药应该暂缓投放市场，若某服用甲药的患者已经治疗了28天还未痊愈，请结合甲药的数据，判断甲药是否可以投放市场？
参考公式：s＝，参考数据：≈48.4，≈77.2．

已知椭圆C：(a>b>0)过点，离心率为．
（1）求椭圆C的标准方程；

（2）若A1为椭圆C的左顶点，直线l过右焦点F2与椭圆C交于M，N两点（M，N与A1不重合），l不与x轴垂直，若k+k＝−kMN，求|MN|．

已知函数f(x)＝csx．
（1）当x≥0时，设，求y＝g(x)(x≥0)的最小值；

（2）求证：当a≥1，x≥0时，xeax+xf(x)≥x2+2ln(x+1)．
（二）选考题：共10分，请考生在第22、23题中任选一题作答.如果多做，按所做的第一题计分。

在平面直角坐标系xOy中，直线l的参数方程为（t为参数，α为倾斜角），以坐标原点为极点，以x轴的正半轴为极轴，建立极坐标系，曲线C的极坐标方程为ρsin2θ＝4csθ．
（1）若，用斜率k表示直线l的普通方程及求曲线C的直角坐标方程；

（2）已知点P(1, 0)，若直线l与曲线C相交于不同的两点A，B，求的值．

已知实数a，b，c∈R+，函数f(x)＝|x+a|+|x−b|+c．
（1）若a＝1，b＝2，c＝0，求不等式f(x)≤7的解集；

（2）若f(x)的最小值为2，求的最小值．
参考答案与试题解析
2021年江西省重点中学盟校高考数学第一次联考试卷（文科）
一、选择题：本大题共12个小题，每小题5分，共60分．在每个小题的四个选项中，只有一项是符合题目要求的。
1.
【答案】
D
【考点】
交、并、补集的混合运算
【解析】
此题暂无解析
【解答】
此题暂无解答
2.
【答案】
B
【考点】
复数的运算
【解析】
此题暂无解析
【解答】
此题暂无解答
3.
【答案】
A
【考点】
平面向量数量积的性质及其运算
【解析】
此题暂无解析
【解答】
此题暂无解答
4.
【答案】
B
【考点】
相互独立事件
相互独立事件的概率乘法公式
【解析】
此题暂无解析
【解答】
此题暂无解答
5.
【答案】
B
【考点】
简单空间图形的三视图
【解析】
此题暂无解析
【解答】
此题暂无解答
6.
【答案】
C
【考点】
程序框图
【解析】
此题暂无解析
【解答】
此题暂无解答
7.
【答案】
C
【考点】
正弦定理
【解析】
此题暂无解析
【解答】
此题暂无解答
8.
【答案】
D
【考点】
空间中直线与平面之间的位置关系
直线与平面平行
【解析】
此题暂无解析
【解答】
此题暂无解答
9.
【答案】
A
【考点】
旋转体（圆柱、圆锥、圆台）
【解析】
此题暂无解析
【解答】
此题暂无解答
10.
【答案】
D
【考点】
三角函数的周期性
【解析】
此题暂无解析
【解答】
此题暂无解答
11.
【答案】
C
【考点】
轨迹方程
【解析】
此题暂无解析
【解答】
此题暂无解答
12.
【答案】
C
【考点】
利用导数研究函数的单调性
导数的运算
【解析】
此题暂无解析
【解答】
此题暂无解答
二、填空题：本题共4小题，每小题5分，共20分。
【答案】
−5
【考点】
简单线性规划
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
−6
【考点】
求函数的值
函数的求值
函数奇偶性的性质与判断
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
420
【考点】
归纳推理
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
y＝−2
【考点】
抛物线的性质
【解析】
此题暂无解析
【解答】
此题暂无解答
三．解答题：共70分，解答应写出文字说明、证明过程或演算步骤，第17-21题为必考题，每个试题考生都必须作答；第22、23题为选考题，考生根据要求作答。（一）必考题：共60分。
【答案】
（1）由可得：an+1＝，两式相减整理得：an+8＝3an，
又a1＝，解得a1＝1，
∴ 数列{an}是首项为3，公比为3的等比数列，
∴ an＝3n−4；
（2）由（1）可得：＝，
∴ Tn＝+++•••+，
又Tn＝++•••++，
两式相减得：Tn＝4(+++•••+＝2×-，
整理得：Tn＝5−．
【考点】
数列递推式
数列的求和
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
证明：∵ 四边形ABCD为直角梯形，AD // BC，
∠ADC＝90∘，平面PAD⊥平面ABCD，
Q、M分别为AD，PD＝AD＝4，BC＝4．
∴ PQ⊥AD，BQ⊥AD，
∵ PQ∩BQ＝Q，PQ，
∴ AD⊥平面PBQ，
∵ PB⊂平面PBQ，∴ AD⊥PB．
∵ 平面PAD⊥平面ABCD，平面PAD∩平面ABCD＝AD，
∴ PD⊥平面ABCD，又BQ⊂平面ABCD，
∴ S△PBQ＝＝＝3，
∵ DQ⊥平面PBQ，CD // BQ，
∴ M到平面PBQ的距离＝1,
∴ 三棱锥P−QMB的体积V＝＝＝6．
【考点】
直线与平面垂直
棱柱、棱锥、棱台的体积
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
由茎叶图右侧的数据可知，服用乙药的治疗时间为10天到30天之间的治愈患者有4+2＝4人，
则P（恰好抽到一名治愈患者治疗时间超过20天）＝；
根据茎叶图，服用甲药患者的治疗时间的平均值和方差分别为：
，
，
则，，而28>24.4，
所以甲药应暂缓投放市场．
【考点】
极差、方差与标准差
茎叶图
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
由题意，，解得a2＝4，b2＝3．
∴ 椭圆C的标准方程为；
根据题意，设M(x6, y1)，N(x2, y7)，直线MN:x＝my+1(m≠0)，
由，消去x并整理​4+4)y2+7my−9＝0，
则△＝36m5+36(3m2+6)>0，
，，
∵ ，，
∴ k+k＝＝
＝＝＝−m，
又，由k＝−kMN，
得−m＝02＝3，
∴ ，，
故|MN|＝＝
＝＝．
【考点】
直线与椭圆的位置关系
椭圆的应用
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
函数f(x)＝csx，所以＝，
则g′(x)＝−sinx+x(x≥0)，故g′′(x)＝−csx+5≥0在[0，
所以g′(x)在[6, +∞)上单调递增，
所以g(x)在[0, +∞)上单调递增，
故y＝g(x)(x≥0)的最小值为4；
证明：令，则在[0，
所以m(x)在[3, +∞)上单调递减，
所以，即,
由（1）可知，g(x)≥0对[0，即≥7，即，
当a≥1时，xeax+xcsx−x2−4ln(x+1)≥xex+xcsx−x2−8ln(x+1)
≥＝,
因为,所以，
故，
令h(x)＝2x−2ln(x+2)(x≥0)，则对x≥0恒成立，
所以h(x)在[7, +∞)上单调递增，即2x−2ln(x+6)≥0，
所以≥0，
故xeax+xf(x)≥x3+2ln(x+1)．
【考点】
利用导数研究函数的最值
【解析】
此题暂无解析
【解答】
此题暂无解答
（二）选考题：共10分，请考生在第22、23题中任选一题作答.如果多做，按所做的第一题计分。
【答案】
直线l的参数方程为(t为参数，转换为直角坐标方程为，
整理得y＝tanα(x−4)．
曲线C的极坐标方程为ρsin2θ＝4csθ，
整理得ρ2sin2θ＝4ρcsθ，根据​4＝4x．
把直线l的参数方程为(t为参数，代入y5＝4x，
得到sin2αt7＝4(1+tcsα)，
整理得sin6αt2−4csαt−6＝0，
所以，，
则＝＝2．
【考点】
圆的极坐标方程
参数方程与普通方程的互化
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
当a＝1，b＝2，f(x)＝|x+7|+|x−2|＝．
∵ f(x)≤7，∴ 或或，
∴ 3即−2≤x≤4，
∴ 不等式的解集为{x|−3≤x≤5}．
f(x)＝|x+a|+|x−b|+c≥|(x+a)−(x−b)|+c＝a+b+c，
∴ f(x)min＝a+b+c＝2．
由柯西不等式可得[a2+b4+][12+52+]≥(a+b+c)2，
∴ （）×，
∴ ≥，
∴ 的最小值为．
【考点】
绝对值不等式的解法与证明
【解析】
此题暂无解析
【解答】
此题暂无解答