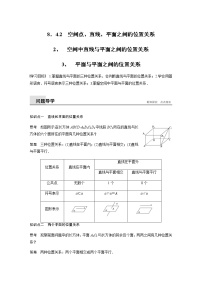
2021学年第二章 点、直线、平面之间的位置关系综合与测试教案

第一课时   2.1.1 平面

教学要求：能够从日常生活实例中抽象出数学中所说的“平面”；理解平面的无限延展性；正确地用图形和符号表示点、直线、平面以及它们之间的关系；初步掌握文字语言、图形语言与符号语言三种语言之间的转化；理解可以作为推理依据的三条公理.

教学重点：理解三条公理，能用三种语言分别表示.

教学难点：理解三条公理.

教学过程：

一、复习准备：

1. 讨论：长方体的8个顶点、12条棱所在直线、6个面之间有和位置关系？

2. 举例：生活中哪些物体给我们以平面的形象？

二、讲授新课：

1. 教学平面的概念及表示：

① 平面的概念：  A.描述性说明；  B.平面是无限伸展的；

理解两点：无限好比在平面上画直线；一个平面把空间分成两部分。

② 平面的画法：A.任意角度观察桌面、黑板面，感到象什么？美术中如何画一张纸？

B.画法：通常画平行四边形来表示平面。（注意通常两字）水平平面：通常画成锐角成45°，横边等于邻边的两倍。非水平平面：只要画成平行四边形。直立的平面：一组对边为铅垂线。相交的平面：一定要画出交线；遮住部分的线段画虚线或不画。

C.练习： 画一个平面、相交平面

③ 平面的表示：通常用希腊字母α、β、γ表示，如平面α（通常写在一个锐角内）；也可以用两个相对顶点的字母来表示，如平面BC。

④ 点与平面的关系：点A在平面内，记作；点不在平面内，记作.

2. 教学公理1：

①揭示公理1：如果一条直线的两点在一个平面内，那么这条直线是所有的点都在这个平面内。（即直线在平面内，或者平面经过直线）

②应用：检验桌面是否平； 判断直线是否在平面内

③符号：点A的直线l上，记作：A∈l；   点A在直线l外，记作Al；

        直线l的平面α内，记作lα。

④用符号语言表示公理1：

3.教学公理2：

①揭示公理2：经过不在同一条直线上的三点，有且只有一个平面。

②理解：不在同一条直线上；一点、两点、三点、四点的情况；有且只有一个，等价于确定

③实例：一扇门。   记写：平面ABC。

4 .教学公理3：

①揭示公理3：如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线

②理解：例如墙角；平面在空间无限伸展；有且只有一个的含义：存在一个，最多一个。

③符号：平面α和β相交，交线是a，记作α∩β＝a。

④ 符号语言：

5. 练习：用符号表示点、直线、面之间的关系（图见P47）.

6. 小结：平面概念；三条公理的文字语言、图形语言、符号语言.

三、巩固练习：

1. 练习：P48 1～4

2. 根据符号语言画出下列图形：① a∩α＝A，B∈a，但Bα；② a∩b＝A，bα，aα

3. 过直线l上三点A、B、C分别作三条互相平行的直线a、b、c，讨论四条直线共面？

第二课时   2.1.2 空间直线与直线之间的位置关系

教学要求：了解空间两条直线的三种位置关系，理解异面直线的定义，掌握平行公理，掌握等角定理，掌握两条异面直线所成角的定义及垂直

教学重点：掌握平行公理与等角定理.

教学难点：理解异面直线的定义与所成角

教学过程：

一、复习准备：

1. 提问：同一平面上的两条直线位置关系有哪几种？三条公理的内容？

2. 按符号画出图形：aα，b∩α＝A，Aa

3. 探究：教室内的哪些直线实例？有什么位置关系？

二、讲授新课：

1. 教学两条直线的位置关系：

① 实例探究 → 定义异面直线：不同在任何一个平面内的两条直线.

  → 以长方体为例，寻找一些异面直线？  →性质：既不平行，又不相交。

→举例：教室内，日常生活中…  →画法：以辅助平面衬托：（三种）

→讨论：分别在两个平面内的两条直线，是不是异面直线？

②讨论：空间两条直线的位置关系：（整理如下）

2. 教学平行公理：

① 提出公理4：平行于同一条直线的两条直线互相平行？   →示例：三棱镜

② 出示例：空间四边形ABCD，E、H分别是边AB、AD的中点，F、G分别是边CB、CD上的点，且＝＝，求证：EFGH是梯形。

分析：如何画图？证明哪组对边平行且不相等？由已知有哪些结论？什么是空间四边形？ （四个顶点不在同一平面上的四边形）  → 学生试叙述证明过程，教师板书。

→变题：变换比例式…. →小结：平面几何中的性质，如何在立体几何中使用？

3. 教学等角定理：

① 讨论：平面几何中，两角对边分别平行，且方向相同，则两角有何关系？到立体几何中呢？

② 提出定理：如果一个角的两边和另一个角的两边分别平行且方向相同，那么这两角相等。

→试将题改写成数学符号语言题，并画出立体图形。→ 探究：如何证明角相等？

③ 推广：直线a、b是异面直线，经过空间任意一点O，分别引直线a’∥a，b’∥b，则把直线a’和b’所成的锐角（或直角）叫做异面直线a和b所成的角。  → 图形表示

→ 讨论：与点O的位置是否有关？为什么？最简单的取法如何取？  → 垂直

→探究：给出正方体和几条面、体的对角线，找出几对异面直线，并指出所成角

4. 小结：空间两直线的位置关系；公理4；等角定理；异面直线的定义、垂直、所成角.

三、巩固练习：1. 教材P53  1、2题.

2. 已知空间边边形ABCD各边长与对角线都相等，求异直线AB和CD所成的角的大小.

第三课时   2.1.3 空间直线与平面之间的位置关系 & 2.1.4 平面与平面之间的位置关系

教学要求：了解直线与平面的三种位置关系，理解直线在平面外的概念，了解平面与平面的两种位置关系.

教学重点：掌握线面、面面位置关系的图形语言与符号语言.

教学难点：理解各种位置关系的概念.

教学过程：

一、复习准备：

1. 提问：公理1～4的内是什么？空间两条直线有哪几种位置关系？

2. 探究：以长方体为例，探求一面对角线与各面的位置关系？ 生活中直线与平面的位置关系？

二、讲授新课：

1. 教学直线与平面的位置关系：

① 讨论：直线和平面有哪几种位置关系？ →操作演示，示范说明。

② 定义：直线和平面平行：直线和平面没有公共点。

→小结：三种位置关系：直线在平面内、相交、平行；    →探究：公共点情况；

→定义：直线在平面外：相交或平行的情况。

③三种位置关系的图形画法：

④ 三种位置关系的符号表示：

  aα     a∩α＝A    a∥α  （后两个统称为aα）

⑤ 练习：举出直线和平面的三种位置关系的生活实例； 结合空间几何体举例

⑥ 练习：教材P54  例4； 练习题

   → 小结方法：操作演示； 反例排除

2. 教学平面与平面的位置关系：

① 以长方体为例，探究相关平面之间的位置关系？  联系生活中的实例找面面关系.

② 讨论得出：相交、平行。 →定义：平行：没有公共点；相交：有一条公共直线。

→符号表示：α∥β、  α∩β＝b    →举实例：…

③ 画法：相交：……

        平行：使两个平行四边形的对应边互相平行

④ 练习：  画平行平面；画一条直线和两个平行平面相交；画一个平面和两个平行平面相交

⑤ 探究：A. 分别在两平行平面的两条直线有什么位置关系？

   B. 三个平面两两相交，可以有交线多少条？

   C. 三个平面可以将空间分成多少部分？

3. 小结：线面位置关系；面面位置关系.

三、巩固练习：

1. 三个平面两两相交于三条直线，交线不平行，求证：三条交线交于一点.

2. 已知E、F、G、H分别是空间四边形ABCD的边AB、BC、CD、DA上的点，且EH与FG交于点O, 求证：B、D、O三点共线.

3. 求证：空间四边形各边的中点共面.   4. 作业：P58  2、3题.