






人教版新课标A选修1-21.2独立性检验的基本思想及其初步应用教学ppt课件
展开问题: 数学家庞加莱每天都从一家面包店买一块1000g 的面包,并记录下买回的面包的实际质量。一年后,这位数学家发现,所记录数据的均值为950g。于是庞加莱推断这家面包店的面包分量不足。
假设“面包分量足”,则一年购买面包的质量数据的平均值应该不少于1000g ;“这个平均值不大于950g”是一个与假设“面包分量足”矛盾的小概率事件;这个小概率事件的发生使庞加莱得出推断结果。
一:假设检验问题的原理
假设检验问题由两个互斥的假设构成,其中一个叫做原假设,用H0表示;另一个叫做备择假设,用H1表示。
例如,在前面的例子中, 原假设为: H0:面包分量足,备择假设为 H1:面包分量不足。这个假设检验问题可以表达为: H0:面包分量足 ←→ H1:面包分量不足
考虑假设检验问题: H0:面包分量足 ←→ H1:面包分量不足
在H0成立的条件下,构造与H0矛盾的小概率事件;如果样本使得这个小概率事件发生,就能以一定把握断言H1成立;否则,断言没有发现样本数据与H0相矛盾的证据。
这种变量的不同取“值”表示个体所属的不同类别,这类变量称为分类变量
对于性别变量,取值为:男、女
分类变量在现实生活中是大量存在的,如是否吸烟,是否患肺癌,宗教信仰,国别,年龄,出生月份等等。
利用随机变量K2来确定在多大程度上可以认为”两个分类变量有关系”的方法称为两个分类变量的独立性检验.(为假设检验的特例)
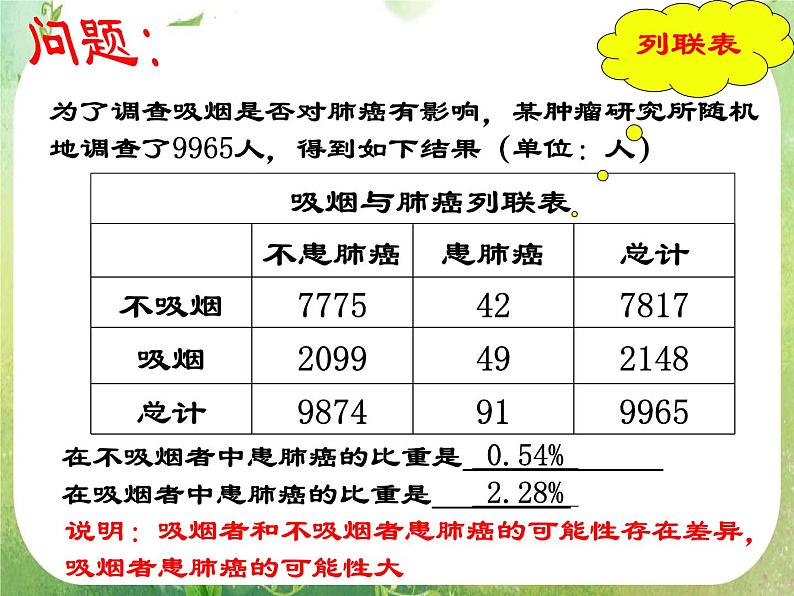
为了调查吸烟是否对肺癌有影响,某肿瘤研究所随机地调查了9965人,得到如下结果(单位:人)
说明:吸烟者和不吸烟者患肺癌的可能性存在差异,吸烟者患肺癌的可能性大
1)通过图形直观判断两个分类变量是否相关:
2) 通过图形直观判断两个分类变量是否相关:
3)通过图形直观判断两个分类变量是否相关:
H0: 吸烟和患肺癌之间没有关系 ←→ H1: 吸烟和患肺癌之间有关系
通过数据和图表分析,得到结论是:吸烟与患肺癌有关
结论的可靠程度如何?
用 A 表示“不吸烟”, B 表示“不患肺癌”
则 H0: 吸烟和患肺癌之间没有关系
“吸烟”与“患肺癌”独立,
作为检验在多大程度上可以认为“两个变量有关系”的标准 。
设有两个分类变量X和Y它们的值域分别为{x1,x2}和{y1,y2}其样本频数列表(称为2×2列联表) 为
现在的K2=56.632的观测值远大于6.635
例1.在某医院,因为患心脏病而住院的665名男性病人中,有214人秃顶,而另外772名不是因为患心脏病而住院的男性病人中有175人秃顶.分别利用图形和独立性检验方法判断是否有关?你所得的结论在什么范围内有效?
例2.为考察高中生性别与是否喜欢数学课程之间的关系,在某城市的某校高中生中随机抽取300名学生,得到如下列联表:
性别与喜欢数学课程列联表
人教版新课标A选修2-33.2独立性检验的基本思想及其初步备课课件ppt: 这是一份人教版新课标A选修2-33.2独立性检验的基本思想及其初步备课课件ppt
人教版新课标A选修2-3第三章 统计案例3.2独立性检验的基本思想及其初步教课内容ppt课件: 这是一份人教版新课标A选修2-3第三章 统计案例3.2独立性检验的基本思想及其初步教课内容ppt课件
2020-2021学年1.2独立性检验的基本思想及其初步应用图文ppt课件: 这是一份2020-2021学年1.2独立性检验的基本思想及其初步应用图文ppt课件,共49页。PPT课件主要包含了不同类别,频数表,x1x2,y1y2,互相影响,频率特征,k≥k0,犯错误的概率,没有发现足够证据,事件A与B是无关的等内容,欢迎下载使用。













