中考数学《一轮专题讲义》（41专题）第18讲 数据的收集与整理（原卷版）学案

这是一份中考数学《一轮专题讲义》（41专题）第18讲 数据的收集与整理（原卷版）学案，共10页。学案主要包含了调查方式，总体，平均数，众数，方差与标准差，频数与频率等内容，欢迎下载使用。
聚焦考点☆温习理解
一、调查方式
1.普查：为了某一特定目的，而对考察对象进行全面的调查，叫普查.
2.抽样调查：抽取一部分对象进行调查，然后根据调查数据推断全体对象的情况.
二、总体、个体、样本及样本容量
(1)总体：把所要考察对象的全体叫总体．
(2)个体：每一个考察对象叫做个体．
(3)样本：从总体中所抽取的一部分个体叫做总体的一个样本．
(4)样本容量：样本中个体的数目叫做样本容量．
三、平均数
(1)平均数：一般地，如果有n个数那么，叫做这n个数的平均数，读作“x拔”。
(2)加权平均数：如果n个数中，出现次，出现次，…，出现次(这里)，那么，根据平均数的定义，这n个数的平均数可以表示为，这样求得的平均数叫做加权平均数，其中叫做权。
四、众数、中位数
1、众数
在一组数据中，出现次数最多的数据叫做这组数据的众数。
2、中位数
将一组数据按大小依次排列，把处在最中间位置的一个数据(或最中间两个数据的平均数)叫做这组数据的中位数。
五、方差与标准差
在一组数据中，各数据与它们的平均数的差的平方的平均数，叫做这组数据的方差。通常用“”表示，即

方差的算数平方根叫做这组数据的标准差，用“s”表示，即
六、频数与频率
①极差：最大值与最小值的差
②频数：落在各个小组内的数据的个数
③频率：每一小组的频数与数据总数(样本容量n)的比值叫做这一小组的频率。
名师点睛☆典例分类
考点典例一、选择合适的调查方式
【例1】(2019·广西贺州·3分)调查我市一批药品的质量是否符合国家标准．采用 方式更合适．(填“全面调查”或“抽样调查”)
【举一反三】
(2017重庆A卷第4题)下列调查中，最适合采用全面调查(普查)方式的是( )
A．对重庆市初中学生每天阅读时间的调查
B．对端午节期间市场上粽子质量情况的调查
C．对某批次手机的防水功能的调查
D．对某校九年级3班学生肺活量情况的调查
考点典例二、总体、个体、样本、样本容量
【例2】(湖南省邵阳县黄亭市镇中学2017~2018学年九年级数学(上)期末检测模拟题)从全区5000份试卷中随机抽取500份试卷，其中300份成绩及格，估计全市成绩及格的人数约为_________人．
【举一反三】
(2018湖南常德一模)彭山的枇杷大又甜，在今年5月18日“彭山枇杷节”期间，从山上5棵枇杷树上采摘到了200千克枇杷，请估计彭山近600棵枇杷树今年一共收获了枇杷 千克．
考点典例三、平均数、众数、中位数的计算
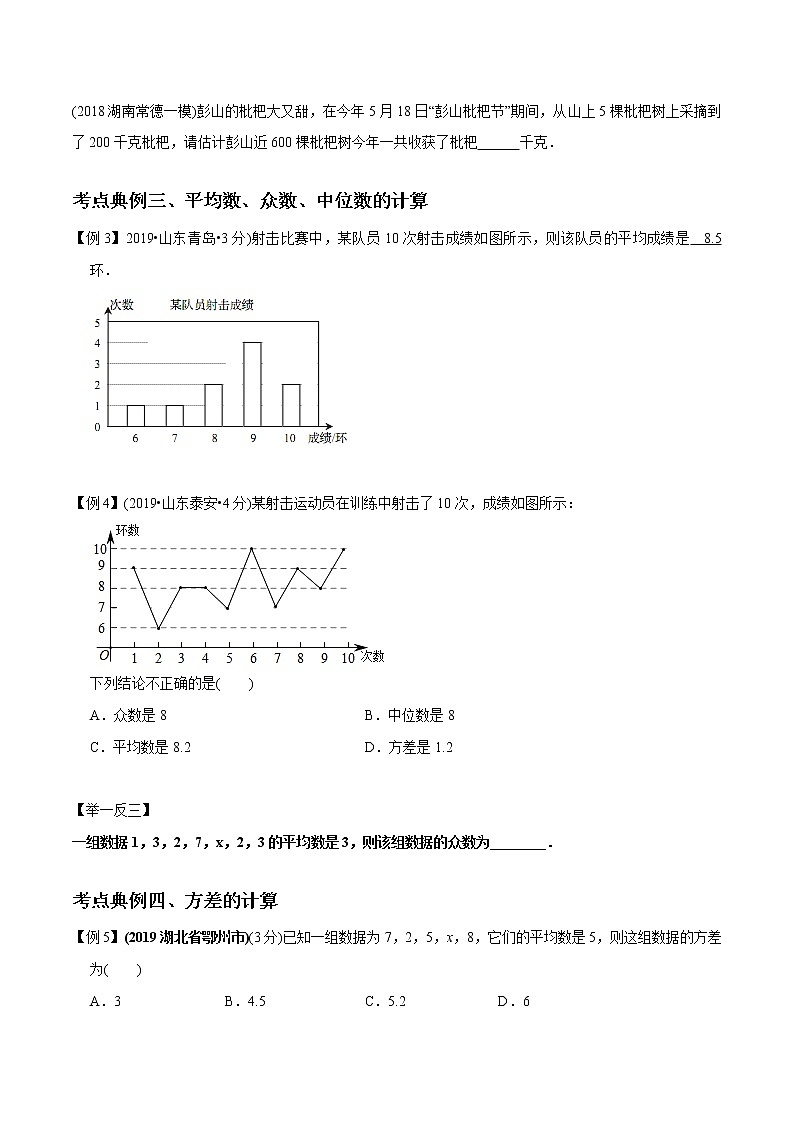
【例3】2019•山东青岛•3分)射击比赛中，某队员10次射击成绩如图所示，则该队员的平均成绩是 8.5 环．
【例4】(2019•山东泰安•4分)某射击运动员在训练中射击了10次，成绩如图所示：
下列结论不正确的是( )
A．众数是8B．中位数是8
C．平均数是8.2D．方差是1.2
【举一反三】
一组数据1，3，2，7，x，2，3的平均数是3，则该组数据的众数为________．
考点典例四、方差的计算
【例5】(2019湖北省鄂州市)(3分)已知一组数据为7，2，5，x，8，它们的平均数是5，则这组数据的方差为( )
A．3B．4.5C．5.2D．6
【举一反三】
1. (2018上海市中考模拟)已知组四人的成绩分别为90、60、90、60，组四人的成绩分别为70、80、80、70，用下列哪个统计知识分析区别两组成绩更恰当( )
A.平均数B.中位数C.众数D.方差
2. (2019•广西北部湾经济区•3分)甲，乙两人进行飞镖比赛，每人各投6次，甲的成绩(单位：环)为：9，8，9，6，10，6．甲，乙两人平均成绩相等，乙成绩的方差为4，那么成绩较为稳定的是______．(填“甲”或“乙”)
考点典例五、利用统计量，解决实际问题
【例6】．(2019•湖南常德•3分)某公司全体职工的月工资如下：
该公司月工资数据的众数为2000，中位数为2250，平均数为3115，极差为16800，公司的普通员工最关注的数据是( )
A．中位数和众数B．平均数和众数
C．平均数和中位数D．平均数和极差
【举一反三】
(2018湖南长沙中考模拟)为从甲乙两名射击运动员中选出一人参加竞标赛，特统计了他们最近10次射击训练的成绩，其中，他们射击的平均成绩为环，方差分别是，从稳定性的角度看， 的成绩更稳定(天“甲”或“乙”)
考点典例六、统计图表的分析
【例7】(2019•湖北省荆门市•10分)高尔基说：“书，是人类进步的阶梯．”阅读可以丰富知识、拓展视野、充实生活等诸多益处．为了解学生的课外阅读情况，某校随机抽查了部分学生阅读课外书册数的情况，并绘制出如下统计图，其中条形统计图因为破损丢失了阅读5册书数的数据．
(1)求条形图中丢失的数据，并写出阅读书册数的众数和中位数；
(2)根据随机抽查的这个结果，请估计该校1200名学生中课外阅读5册书的学生人数；
(3)若学校又补查了部分同学的课外阅读情况，得知这部分同学中课外阅读最少的是6册，将补查的情况与之前的数据合并后发现中位数并没有改变，试求最多补查了多少人？
【举一反三】
4月23日是世界读书日，习近平总书记说：“读书可以让人保持思想活力，让人得到智慧启发，让人滋养浩然之气。”某校响应号召，鼓励师生利用课余时间广泛阅读，该校文学社为了解学生课外阅读的情况，抽样调查了部分学生每周用于课外阅读的时间，过程如下：
收集数据 从学校随机抽取20名学生，进行了每周用于课外阅读时间的调查，数据如下(单位：min):
30 60 81 50 40 110 130 146 90 100
60 81 120 140 70 81 10 20 100 81
整理数据 按如下分段整理样本数据并补全表格：
分析数据 补全下列表格中的统计量：
得出结论
(1)用样本中的统计量估计该校学生每周用于课外阅读时间的情况等级为 ；
(2)如果该校现有学生400人，估计等级为“”的学生有多少名？
(3)假设平均阅读一本课外书的时间为160分钟，请你选择一种统计量估计该校学生每人一年 (按52周计算)平均阅读多少本课外书？
课时作业☆能力提升
1. (2018湖南常德中考模拟)株洲市展览馆某天四个时间段进出馆人数统计如下，则馆内人数变化最大时间段为( )
A．9：00﹣10：00B．10：00﹣11：00C．14：00﹣15：00D．15：00﹣16：00
2. (2109山东潍坊)小莹同学10个周综合素质评价成绩统计如下：
这10个周的综合素质评价成绩的中位数和方差分别是( )
A．97.5 2.8B．97.5 3
C．97 2.8D．97 3
3. 某班组织了针对全班同学关于“你最喜欢的一项体育活动”的问卷调查后，绘制出频数分布直方图，由图可知，下列结论正确的是
A. 最喜欢篮球的人数最多 B. 最喜欢羽毛球的人数是最喜欢乒乓球人数的两倍
C. 全班共有50名学生 D. 最喜欢田径的人数占总人数的10 %
4. (2018湖南长沙中考模拟)如图是根据我市某天七个整点时的气温绘制成的统计图，则这七个整点时气温的中位数和平均数分别是( )
A．30，28 B．26，26 C．31，30 D．26，22
来源:ZXXK]
5. 某中学九年级二班六级的8名同学在一次排球垫球测试中的成绩如下(单位：个)
35 38 42 44 40 47 45 45
则这组数据的中位数、平均数分别是( )
A. 42、42 B. 43、42 C. 43、43 D. 44、43
6. 为考察两名实习工人的工作情况，质检部将他们工作第一周每天生产合格产品的个数整理成甲，乙两组数据，如下表：
关于以上数据，说法正确的是( )
A. 甲、乙的众数相同 B. 甲、乙的中位数相同
C. 甲的平均数小于乙的平均数 D. 甲的方差小于乙的方差
7. (2018年湖北省黄冈市黄州区路口中学数学中考模拟试题(一))如图为某班35名学生投篮成绩的长条图，其中上面部分数据破损导致数据不完全．已知此班学生投篮成绩的中位数是5，则根据图，无法确定下列哪一选项中的数值( )
A. 3球以下(含3球)的人数 B. 4球以下(含4球)的人数
C. 5球以下(含5球)的人数 D. 6球以下(含6球)的人数
8. (2018年湖南省郴州市资兴市兴华实验学校中考数学模拟试卷)如图是地球表面的一部分，扇形A表示地球某几种水域占总面积的40%，则此扇形的圆心角为________．

10. (2018黑龙江绥化中考模拟)在一次射击训练中，某位选手五次射击的环数分别为5，8，7，6，9．则这位选手五次射击环数的方差为 ．
11. (2019湖南张家界)为了建设“书香校园”，某校七年级的同学积极捐书，下表统计了
七(1)班40名学生的捐书情况：
该班学生平均每人捐书 本．
12. 某校拟招聘一名优秀数学教师，现有甲、乙、丙三名教师入围，三名教师师笔试、面试成绩如右表所示，综合成绩按照笔试占60%、面试占40%进行计算，学校录取综合成绩得分最高者，则被录取教师的综合成绩为分_____．
13. 随机抽取某理发店一周的营业额如下表(单位：元)：
(1)求该店本周的日平均营业额.
(2)如果用该店本周星期一到星期五的日平均营业额估计当月的营业总额，你认为是否合理？如果合理，请说明理由；如果不合理，请设计一个方案，并估计该店当月(按30天计算)的营业总额.
14. (2018年湖北省黄梅濯港镇中心学校数学中考模拟试题)某县教育局为了丰富初中学生的大课间活动，要求各学校开展形式多样的阳光体育活动．某中学就“学生体育活动兴趣爱好”的问题，随机调查了本校某班的学生，并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图：
(1)在这次调查中，喜欢篮球项目的同学有 人，在扇形统计图中，“乒乓球”的百分比为 %，如果学校有800名学生，估计全校学生中有 人喜欢篮球项目．
(2)请将条形统计图补充完整．
(3)在被调查的学生中，喜欢篮球的有2名女同学，其余为男同学．现要从中随机抽取2名同学代表班级参加校篮球队，请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率．
15. (2018年湖北省宜昌市夷陵区东湖初级中学数学中考模拟试题(一))学生小明、小华为了解本校八年级学生每周上网的时间，各自进行了抽样调查．小明调查了八年级信息技术兴趣小组中40名学生每周上网的时间，算得这些学生平均每周上网时间为2.5h；小华从全体320名八年级学生名单中随机抽取了40名学生，调查了他们每周上网的时间，算得这些学生平均每周上网时间为1.2h．小明与小华整理各自样本数据，如表所示．
(每组可含最低值，不含最高值)
请根据上述信息，回答下列问题：
(1)你认为哪位学生抽取的样本具有代表性？_____．
估计该校全体八年级学生平均每周上网时间为_____h；
(2)在具有代表性的样本中，中位数所在的时间段是_____h/周；
(3)专家建议每周上网2h以上(含2h)的同学应适当减少上网的时间，根据具有代表性的样本估计，该校全体八年级学生中有多少名学生应适当减少上网的时间？
月工资(元)
18000
12000
8000
6000
4000
2500
2000
1500
1200
人数
1(总经理)
2(副总经理)
3
4
10
20
22
12
6
课外阅读时间x(min)
等级
D
C
B
A
人数
3
8
平均数
中位数
众数
80
9：00﹣10：00
10：00﹣11：00
14：00﹣15：00
15：00﹣16：00
进馆人数
50
24
55
32
出馆人数
30
65
28
45
成绩(分)
94
95
97
98
100
周数(个)
1
2
2
4
1
甲
2
6
7
7
8
乙
2
3
4
8
8
捐书(本)
3
4
5
7
10
人数
5
7
10
11
7
星期一
星期二
星期三
星期四
星期五
星期六
星期日
合计
540
680
760
640
960
2200
1780
7560
时间段(h/周)
小明抽样人数
小华抽样人数
0～1
6
22
1～2
10
10
2～3
16
6
3～4
8
2