高中数学人教版新课标B必修13.1.1实数指数幂及其运算授课课件ppt
展开3.1 指数与指数函数
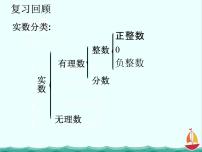
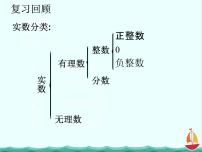
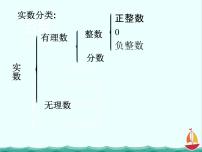
3.1.1 实数指数幂及其运算
(3)分数指数幂,规定正数的正分数指数幂的意义是________________.正数的负分数指数幂的意义与负整数指数幂的意义相同,规定:__________________,0的正分数指数幂等于0,0的负分数指数幂没有意义.(4)设a>0,b>0,对任意有理数α、β,有理数幂有如下三条运算法则:aα·aβ=________,(aα)β=________,(ab)α=________.
分析:先把负整数指数幂化为正整数指数幂,得到熟悉的繁分式再化简.
评析:同底数的幂做乘法、除法、乘方、开方时常化为有理数指数运算.不同底数的多个项做除法运算时,化为正数指数运算化简更简单.
变式训练 1 化简(a3+a-3)(a3-a-3)÷[(a4+a-4+1)(a-a-1)].
题型二 化简求值【例2】 已知:x-3+1=a,求:a2-2ax-3+x-6的值.分析:所求的式子比较复杂,但如果我们把已知条件x-3+1视为一个整体,则能迅速求解.解:a2-2ax-3+x-6=(a-x-3)2=12=1.评析:这类题目一般是先化简,再求值.在化简的过程中,联系已知条件,整体代入,问题获得迅速解决.
题型三 分数指数幂的运算【例3】 求值:分析:先化简,将各式子的结构统一到假分数和真分数的形式,然后寻找规律,利用分数指数幂的性质进行计算,要注意公式的正用、逆用和活用.
评析:计算题也遵循“先化简后求值”的原则,在计算中要写出必要的步骤,一步解决一个问题,这是避免出错的一种好方法.
题型四 分数指数幂的化简分析:第(1)小题可以将根式化为分数指数幂,然后化简;第(2)小题可以先用分数指数的运算性质进行计算;第(3)小题可以先将完全平方式展开,进行化简,从而发现规律,再化简.
变式训练 4 化简:分析:观察所给各式子的结构特征,联想立方和、差与平方差公式,即可找到解题思路.
评析:注意灵活应用分式化简的方法和技巧.(1)把分子、分母分解因式,可约分的先约分;(2)利用公式的基本性质化繁分式为最简分式,化异分母为同分母;③把适当的几个分式先化简,各个击破;④用换元法,使分式简化.
分析:判断命题的真假,主要考查命题成立的条件,因此,要对照有关的定义和性质,全面考虑定义和性质的特点,牢记使用范围,才能作出判断.
评析:(1)要说明一个命题是假命题,只要举出一个反例即可.(2)注意课本内容的理解,在“根式”部分,xn=a中的a,根据不同情况,可以取负值,但在“分数指数幂”部分, 中的a必须取正数,在这部分的概念和性质中,都有a>0.
解:先把根式化成分数指数幂的形式,再计算:
分析:(1)式应将根式化为分数指数幂进行运算.(2)、(3)式观察可知,要利用立方差公式a3-b3=(a-b)(a2+ab+b2).
评析:解决化简问题时常用公式有:①a2-b2=(a+b)(a-b);②a2+b2=(a+b)2-2ab;a2+b2=(a-b)2+2ab;③(a+b)2=a2+2ab+b2;将b换成-b,有(a-b)2=a2-2ab+b2;④a3+b3=(a+b)(a2-ab+b2);将b换成-b,有a3-b3=(a-b)(a2+ab+b2);⑤(a+b)3=a3+3a2b+3ab2+b3;将b换成-b,有(a-b)3=a3-3a2b+3ab2-b3.
评析:(1)解题思路的由来:观察所求结果,式子的结构是分式,而分子、分母没有公因式,因此必然是找出x与y的关系,使分子、分母约分,达到化简的目的.(2)已知条件中,x与y的关系复杂,必然可以找到规律,化复杂为简单.而这个规律就是将已知条件的一边分解成因式相乘,使另一边为0,达到化简条件的目的.
题型二 有理指数幂的应用【例2】 (数学与日常生活)有一位大学生毕业后到一家私营企业去工作,试用期过后,老板对这位大学生很赞赏,有意留下他,就让这位大学生提出待遇方面的要求,这位学生提出了两种方案让老板选择,其一:工作一年,月薪5000元;其二:工作一年,第一个月的工资为20元,以后每个月的工资是上月工资的2倍.此时老板不假思索就选了第二种方案,于是他们之间就定了一个劳动待遇合同,一年之后,这位老板才发现自己选择了错误的方案,这是为什么?分析:两种方案分别求出一年的工资总和.
解:第一种方案:S1=5000×12=60000(元).第二种方案:S2=20+20×2+20×22+…+20×211=81900(元).S2>S1因此选第一种方案更合算.评析:关于S2的求和,在后面的数列中我们将学习一种较为简单的求和公式.
分析:化根式为分数指数幂,运用分数指数幂的运算性质求解.
r=0、4、8时,上式成为关于a的整数指数幂.评析:(1)本题中确定整数指数幂时,可由r的范围从小到大依次验证,决定取舍.(2)利用分数指数幂进行根式计算时,结果可化为根式形式或保留分数指数幂的形式,但不能既有根式又有分数指数幂.
题型四 利用分数指数幂的运算法则证明恒等式
分析:第(1)题左边有两项,右边有一项,该题的证明应该遵循“化繁为简”、“化异为同”的原则,将左边提取公因式以减少项数,向右边推进.第(2)题的条件中有连等式,我们常用的方法是设出一个字母当基本量,其他的字母或关系式都用这个字母来表示,使各个式子都找到“共同语言”,然后代入所证的式子进行化简.
评析:(1)本题右边的式子就是我们的证明方向.左边的式子,首先在两项的内部,根据它们共同的结构,分别提出公因式,则整个左边的式子就立即显露出公因式,因此,要敢于尝试,勇于探索.(2)①通过引入字母t,使ax2,by2,cz2都与t产生联系,都化为与t有关的式子,从而使整个等式的左边产生公因式,这种解题技巧值得学习.
1.实数指数幂及其运算(1)课件PPT: 这是一份1.实数指数幂及其运算(1)课件PPT,共28页。
高中数学3.1.1实数指数幂及其运算课前预习课件ppt: 这是一份高中数学3.1.1实数指数幂及其运算课前预习课件ppt,共24页。PPT课件主要包含了1整数指数幂,a+b,2分数指数幂,1n次方根的定义,偶次方根有以下性质,奇次方根有以下性质,基础练习3,答案61-3a,7b-aa-b,基础练习4等内容,欢迎下载使用。
数学必修13.1.1实数指数幂及其运算图片课件ppt: 这是一份数学必修13.1.1实数指数幂及其运算图片课件ppt,共19页。PPT课件主要包含了实数指数幂及其运算,正整数指数幂,整数指数幂,分数指数,根式性质,练习1,分数指数幂,有理数指数幂,运算法则,练习2等内容,欢迎下载使用。