人教版新课标B必修52.1.1数列课后复习题

课题：数列的综合应用

教学目标：熟练掌握等差（比）数列的基本公式和一些重要性质，并能灵活运用性质解决有关的问题，培养对知识的转化和应用能力．

教学重点：等差（比）数列的性质的应用． 

（一） 主要知识： 

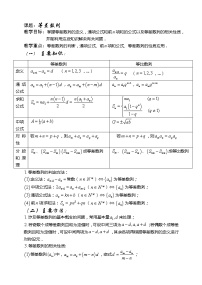
等差数列的概念、性质及基本公式。等比数列的概念、性质及基本公式。

（二）主要方法：

解决等差数列和等比数列的问题时，通常考虑两类方法：①基本量法：即运用条件转化为关于和的方程；②巧妙运用等差数列和等比数列的性质，一般地运用性质可以化繁为简，减少运算量．

深刻领会两类数列的性质，弄清通项和前项和公式的内在联系是解题的关键．

解题时，还要注重数学思想方法的应用，如“函数与方程”、“数形结合”、“分类讨论”、

“化归转化”.

（三）典例分析：

问题1． （湖北）若互不相等的实数、、成等差数列，、、成等比数列，且，则                 

(天津)设等差数列的公差不为，．若是与的等比中项，则                                  

（海南）已知，，成等差数列，成等比数列，则的最小值是                       

已知等差数列的公差，且成等比数列，则      

(全国Ⅰ)等比数列的前项和为，已知，，成等差数列，

则的公比为                  

问题2．(全国Ⅰ文)设是等差数列，是各项都为正数的等比数列，且，，

求，的通项公式；求数列的前项和．

问题3．（全国Ⅲ）在等差数列中，公差，是与的等比中项，已知数列成等比数列，求数列的通项

问题4．（届东北师大附中高三月考）数列的前项和记作，满足，．

   证明数列为等比数列；并求出数列的通项公式．

   记，数列的前项和为，求．

问题5.（上海） 已知数列（为正整数）是首项是，公比为的等比数列.

   求和：

   由的结果归纳概括出关于正整数的一个结论，并加以证明.

（四）巩固练习：

（上海）在等差数列中，若，则有不等式

成立，相应地：在等比数列，若，
则有不等式                                                      成立.

（北京）定义“等和数列”：在一个数列中，如果每一项与它的后一项的和都为同一个常数，那么这个数列叫做等和数列，这个常数叫做该数列的公和. 已知数列是等和数列，且，公和为，那么的值为____，这个数列的前项和的计算公式为_______

（新课程）设是公比为的等比数列，是它的前项和，若是等差数列，则          

有四个数，其中前三个数成等差数列，后三个数成等比数列，且第一个数与第四个数的和是，第二个数与第三个数的和是，求这四个数．　　　　　　　　　　　　　

（五）课后作业：

 (浙江文）若是公差不为的等差数列的前项和，且成等比数列.求数列的公比;若，求的通项公式.

（福建）已知是公比为的等比数列，且成等差数列.

求的值；设{}是以为首项，为公差的等差数列，其前项和为，当≥时，比较与的大小，并说明理由.

（六）走向高考：

（陕西）已知各项全不为零的数列的前项和为，且，其中．求数列的通项公式；对任意给定的正整数，数列满足（），，求．

（湖北文）设数列的前项和为，为等比数列，且，，求数列和的通项公式；

   设，求数列的前项和

（陕西文）已知实数列是等比数列，其中，且，，成等差数列．（Ⅰ）求数列的通项公式；

（Ⅱ）数列的前项和记为，证明：．

（湖南文）设是数列（）的前项和，，且，，．

（Ⅰ）证明：数列（）是常数数列；

（Ⅱ）试找出一个奇数，使以为首项，为公比的等比数列（）中的所有项都是数列中的项，并指出是数列中的第几项．

[

（北京）在数列中，若是正整数，且，

则称为“绝对差数列”.举出一个前五项不为零的“绝对差数列”（只要求写出前十项）； 若“绝对差数列”中，，数列满足，，分别判断当时，与的极限是否存在，如果存在，求出其极限值；证明：任何“绝对差数列”中总含有无穷多个为零的项.

（上海）如果有穷数列（为正整数）满足条件，，…，，即（），我们称其为“对称数列”．

例如，数列与数列都是“对称数列”．

设是项的“对称数列”，其中是等差数列，且，．依次写出的每一项；

设是项的“对称数列”，其中是首项为，公比为的等比数列，求各项的和；

设是项的“对称数列”，其中是首项为，公差为的等差数列．求前项的和．