高中数学2.1指数函数学案

指数与指数函数

●知识梳理

1.指数

（1）n次方根的定义

若xn=a，则称x为a的n次方根，“”是方根的记号.

在实数范围内，正数的奇次方根是一个正数，负数的奇次方根是一个负数，0的奇次方根是0；正数的偶次方根是两个绝对值相等符号相反的数，0的偶次方根是0，负数没有偶次方根.

（2）方根的性质

①当n为奇数时，=a.

②当n为偶数时，=|a|=

（3）分数指数幂的意义

①a=（a＞0，m、n都是正整数，n＞1）.

②a==（a＞0，m、n都是正整数，n＞1）.

2.指数函数

（1）指数函数的定义

一般地，函数y=ax（a＞0且a≠1）叫做指数函数.

（2）指数函数的图象

底数互为倒数的两个指数函数的图象关于y轴对称.

（3）指数函数的性质

①定义域：R.

②值域：（0，＋∞）.

③过点（0，1），即x=0时，y=1.

④当a＞1时，在R上是增函数；当0＜a＜1时，在R上是减函数.

●点击双基

1.·等于

A.－               B.－

C.          D.

解析：·=a·（－a）=－（－a）=－（－a）.

答案：A

2.（2003年郑州市质量检测题）函数y=2的图象与直线y=x的位置关系是

解析：y=2=（）x.

∵＞1，∴不可能选D.

又∵当x=1时，2＞x，而当x=3时，2＜x，∴不可能选A、B.

答案：C

3.（2004年湖北，文5）若函数y=ax+b－1（a＞0且a≠1）的图象经过二、三、四象限，则一定有

A.0＜a＜1且b＞0       B.a＞1且b＞0

C.0＜a＜1且b＜0       D.a＞1且b＜0

解析：作函数y=ax+b－1的图象.

答案：C

4.（2004年全国Ⅱ，理6）函数y=－ex的图象

A.与y=ex的图象关于y轴对称    B.与y=ex的图象关于坐标原点对称

C.与y=e－x的图象关于y轴对称    D.与y=e－x的图象关于坐标原点对称

解析：图象法.

答案：D

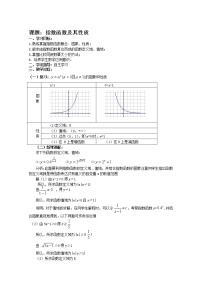
5.（2004年湖南，文16）若直线y=2a与函数y=|ax－1|（a＞0且a≠1）的图象有两个公共点，则a的取值范围是___________________.

解析：数形结合.由图象可知0＜2a＜1，0＜a＜.

答案：0＜a＜

6.函数y=（）的递增区间是___________.

解析：∵y=（）x在（－∞，+∞）上是减函数，而函数y=x2－2x+2=（x－1）2+1的递减区间是（－∞，1］，∴原函数的递增区间是（－∞，1］.

答案：（－∞，1］

●典例剖析

【例1】 下图是指数函数（1）y=ax，（2）y=bx，（3）y=cx，（4）y=dx的图象，则a、b、c、d与1的大小关系是

A.a＜b＜1＜c＜d       B.b＜a＜1＜d＜c

C.1＜a＜b＜c＜d       D.a＜b＜1＜d＜c

剖析：可先分两类，即（3）（4）的底数一定大于1，（1）（2）的底数小于1，然后再从（3）（4）中比较c、d的大小，从（1）（2）中比较a、b的大小.

解法一：当指数函数底数大于1时，图象上升，且当底数越大，图象向上越靠近于y轴；当底数大于0小于1时，图象下降，底数越小，图象向右越靠近于x轴.得b＜a＜1＜d＜c.

解法二：令x=1，由图知c1＞d1＞a1＞b1，

∴b＜a＜1＜d＜c.

答案：B

【例2】 已知2≤（）x－2，求函数y=2x－2－x的值域.

解：∵2≤2－2（x－2），∴x2+x≤4－2x，即x2+3x－4≤0，得－4≤x≤1.又∵y=2x－2－x是［－4，1］上的增函数，∴2－4－24≤y≤2－2－1.故所求函数y的值域是［－，］.

【例3】 要使函数y=1+2x+4xa在x∈（－∞，1］上y＞0恒成立，求a的取值范围.

解：由题意，得1+2x+4xa＞0在x∈（－∞，1］上恒成立，即a＞－在x∈（－∞，1］上恒成立.又∵－=－（）2x－（）x=－［（）x+］2+，当x∈（－∞，1］时值域为（－∞，－］，∴a＞－.

评述：将不等式恒成立问题转化为求函数值域问题是解决这类问题常用的方法.

●闯关训练

夯实基础

1.已知f（x）=ax，g（x）=－logbx，且lga+lgb=0，a≠1，b≠1，则y=f（x）与y=g（x）的图象

A.关于直线x+y=0对称      B.关于直线x－y=0对称

C.关于y轴对称       D.关于原点对称

解析：lga+lgb=0ab=1.

∴g（x）=－logbx=－loga－1x=logax.

∴f（x）与g（x）的图象关于y=x对称.

答案：B

2.下列函数中值域为正实数的是

A.y=－5x         B.y=（）1－x

C.y=       D.y=

解析：∵y=（）x的值域是正实数，而1－x∈R，∴y=（）1－x的值域是正实数.

答案：B

3.化简（a＞0，b＞0）的结果是___________________.

解析：原式====.

答案：

4.满足条件m＞（mm）2的正数m的取值范围是___________________.

解析：∵m＞0，∴当m＞1时，有m2＞2m，即m＞2；

当0＜m＜1时，有m2＜2m，即0＜m＜1.

综上所述，m＞2或0＜m＜1.

答案：m＞2或0＜m＜1

5.（2004年湖北，理7）函数f（x）=ax+loga（x+1）在［0，1］上的最大值与最小值的和为a，则a的值为

A.         B.         C.2         D.4

解析：f（x）在［0，1］上是单调函数，由已知f（0）+f（1）=a1+loga1+a+loga2=aloga2=－1a=.

答案：B

6.已知9x－10·3x+9≤0，求函数y=（）x－1－4（）x+2的最大值和最小值.

解：由9x－10·3x+9≤0得（3x－1）（3x－9）≤0，解得1≤3x≤9.∴0≤x≤2.令（）x=t，则≤t≤1，y=4t2－4t+2=4（t－）2+1.当t=即x=1时，ymin=1；当t=1即x=0时，ymax=2.

培养能力

7.若a2x+·ax－≤0（a＞0且a≠1），求y=2a2x－3·ax+4的值域.

解：由a2x+·ax－≤0（a＞0且a≠1）知0＜ax≤.

令ax=t，则0＜t≤，y=2t2－3t+4.借助二次函数图象知y∈［3，4）.

8.（2004年全国Ⅲ，18）解方程4x+|1－2x|=11.

解：当x≤0时，1－2x≥0.

原方程4x－2x－10=02x=±2x=－＜0（无解）或2x=+＞1知x＞0（无解）.

当x＞0时，1－2x＜0.

原方程4x+2x－12=02x=－±2x=－4（无解）或2x=3x=log23（为原方程的解）.

探究创新

9.若关于x的方程25－|x+1|－4·5－|x+1|－m=0有实根，求m的取值范围.

解法一：设y=5－|x+1|，则0＜y≤1，问题转化为方程y2－4y－m=0在（0，1］内有实根.设f（y）=y2－4y－m，其对称轴y=2，∴f（0）＞0且f（1）≤0，得－3≤m＜0.

解法二：∵m=y2－4y，其中y=5－|x+1|∈（0，1］，∴m=（y－2）2－4∈［－3，0）.

●思悟小结

1.利用分数指数幂的意义可以把根式的运算转化为幂的运算，从而简化计算过程.

2.指数函数y=ax（a＞0，a≠1）的图象和性质受a的影响，要分a＞1与0＜a＜1来研究.

3.指数函数的定义重在“形式”，像y=2·3x，y=2，y=3，y=3x+1等函数都不符合形式y=ax（a＞0，a≠1），因此，它们都不是指数函数.

●教师下载中心

教学点睛

1.本小节的重点是指数函数的图象和性质的应用.对于含有字母参数的两个函数式比较大小或两个函数式由于自变量的不同取值而有不同大小关系时，必须对字母参数或自变量取值进行分类讨论.用好用活指数函数单调性，是解决这一类问题的关键.

2.对可化为a2x+b·ax+c=0或a2x+b·ax+c≥0（≤0）的指数方程或不等式，常借助换元法解决，但应提醒学生注意换元后“新元”的范围.

拓展题例

【例1】 若60a＝3，60b＝5.求12的值.

解：a=log603，b＝log605，

1－b＝1－log605＝log6012，

1－a－b＝1－log603－log605＝log604，

＝＝log124，

12＝12＝12＝2.

【例2】 方程2x=2－x的解的个数为______________.

解析：方程的解可看作函数y=2x和y=2－x的图象交点的横坐标，分别作出这两个函数图象（如下图）.

由图象得只有一个交点，因此该方程只有一个解.

答案：1

评述：无法直接求解的方程问题，常用作图法来解，注意数形结合的思想.