沪教版高中二年级 第一学期9.4三阶行列式教案

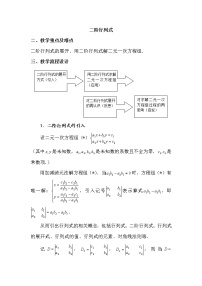
这是一份沪教版高中二年级 第一学期9.4三阶行列式教案，共39页。PPT课件主要包含了本章知识结构图，回章目录，１矩阵的定义，零矩阵，行矩阵，列矩阵，上三角方阵，下三角方阵，对角方阵，数量矩阵等内容，欢迎下载使用。
元素为实数的称为实矩阵,
元素为复数的称为复矩阵.
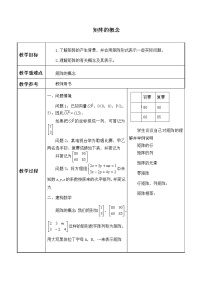
2. 几种特殊矩阵
行数列数皆相等的矩阵。
非零元素只可能在主对角线及其上方。
非零元素只可能在主对角线及其下方.
主对角线上全为1的对角方阵.
行数和列数均相等的矩阵.
阵,且各对应元素也相同,即
矩阵的线性运算的运算规律:
矩阵的分块，主要目的在于简化运算及便于论证．
分块矩阵的运算规则与普通矩阵的运算规则相似．
一、矩阵的运算 二、有关逆矩阵的运算及证明 三、矩阵方程及其求解方法
矩阵运算有其特殊性，若能灵活地运用矩阵的运算性质及运算规律，可极大地提高运算效率.
二、有关逆矩阵的运算及证明
3. 利用分块矩阵求逆阵
注：1. 矩阵的逆阵是线性代数中非常重要的一个内容，主要包括：
①证明矩阵 可逆；②求逆阵；③证明矩阵 是矩
2. 证明矩阵 A 可逆，可利用 A 的行列式不为零或找一个矩阵 B，使 AB=E 或 BA=E 等方法；对数字矩阵，若求其逆阵，一般用 A*(如2阶矩阵)或初等变换(3阶及3阶以上的方阵)的方法来做，有时也利用分块矩阵来做.对抽象的矩阵 A，若求其逆，一般是用定义或 A*来做；证明矩阵 B 是矩阵 A 的逆阵，只需验证 AB=E 或 BA=E 即可.
三. 矩阵方程及其求解方法
一、填空题(8分/题)
二. 证明题 (26分)