华师大版初中数学八年级上册第三次月考快速提分卷 （11-14章）

这是一份华师大版初中数学八年级上册第三次月考快速提分卷 （11-14章），共6页。试卷主要包含了单选题，填空题，计算题，作图题，解答题等内容，欢迎下载使用。
 华师大版初中数学八年级上册第三次月考快速提分卷（11-14章）考试时间：120分钟 满分：120分

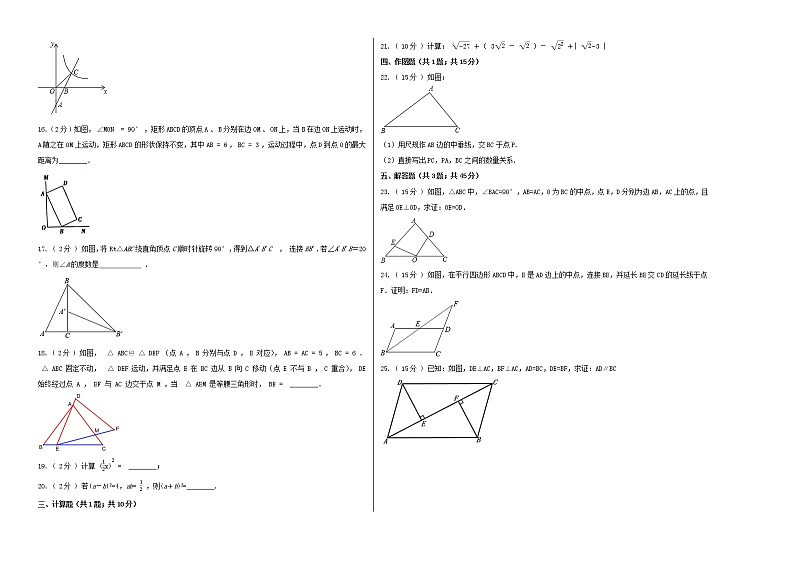
姓名：__________ 班级：__________考号：__________一、单选题（共10题；共30分）1. ( 3分 ) 下列运算正确的是（　　）            A. a6÷a3＝a3    B. a2•a4＝a8   C. 3a2﹣a2＝3   D. （﹣ab2）3＝﹣a3b52. ( 3分 ) 下列计算正确的是（   ）            A.      B. （a2）3＝a5     C. a﹣1÷a﹣3＝a2      D. （a+b）2＝a2+b23. ( 3分 ) 下列运算正确的是（  ）            A.       B.      C.    D. 4. ( 3分 ) 如图，菱形 的边 的垂直平分线交 于点 ，交 于点 ，连接 ．当 时，则 （   ） A. 15°        B. 30°     C. 40°        D. 50°5. ( 3分 ) 下列计算正确的是（   ）            A.    B. 9a3÷3a3＝3a3    C. 2a3+3a3＝5a6   D. （﹣a3）2＝﹣a66. ( 3分 ) 如果 ，那么a.b的值分别为（     ）            A. 2；4    B. 5；-25     C. -2；25     D. -5；257. ( 3分 ) 如图，在△ABC中，∠A=90°，D是AB的中点，过点D作BC的平行线交AC于点E，作BC的垂线交BC于点F，若AB=CE，且△DFE的面积为1，则BC的长为（   ） A.         B. 5        C. 4        D. 108. ( 3分 ) 下列四组线段中，可以构成直角三角形的是（    ）            A.         B.          C.      D. 9. ( 3分 ) 如图，在 中，点 在 上，沿 将 对折，点 与点 重合，则图中全等的三角形有（   ）  A.  对       B.  对       C.  对      D.  对10. ( 3分 ) 如图，在△ABC中，AB＝AC，BC＝10，S△ABC＝60，AD⊥BC于点D，EF垂直平分AB，交AB于点E，AC于点F，在EF上确定一点P，使PB＋PD最小，则这个最小值为（    ）  A. 10       B. 11        C. 12          D. 13二、填空题（共10题；共20分）11. ( 2分 ) 实数 的整数部分是________.    12. ( 2分 ) 计算： 的结果是________.    13. ( 2分 ) 已知正三角形的边心距为 ，那么它的边长为________．    14. ( 2分 ) 一个游泳爱好者要横跨- -条宽AC=8 m的河流，由于水流速度的原因，这位游泳爱好者向下游偏离了BC=6 m，这位游泳爱好者在横跨河流的实际游泳距离为      米．   15. ( 2分 ) 如图，直线y＝ax+b（a≠0）与x轴交于点B  ， 与y轴交于点A  ， 与双曲线y＝ （k≠0）交于点C  ， 若AB＝BC  ， △AOC的面积为4，则k的值是________．  16. ( 2分 ) 如图， ，矩形 的顶点 、 分别在边 、 上，当 在边 上运动时， 随之在 上运动，矩形 的形状保持不变，其中 ， ，运动过程中，点 到点 的最大距离为________．  17. ( 2分 ) 如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A'B'C  ， 连接BB'．若∠A'B'B＝20°，则∠A的度数是       ．  18. ( 2分 ) 如图， （点 ， 分别与点 ， 对应）， ， ． 固定不动， 运动，并满足点 在 边从 向 移动（点 不与 ， 重合）， 始终经过点 ， 与 边交于点 ，当 是等腰三角形时， ________．  19. ( 2分 ) 计算 ________；    20. ( 2分 ) 若(a－b)2=4，ab= ，则(a＋b)2=________.    三、计算题（共1题；共10分）21. ( 10分 ) 计算： ＋（ － ）－ ＋| |    四、作图题（共1题；共15分）22. ( 15分 ) 如图：  （1）用尺规作AB边的中垂线，交BC于点P.    （2）直接写出PC，PA，BC之间的数量关系.    五、解答题（共3题；共45分）23. ( 15分 ) 如图，△ABC中，∠BAC=90°，AB=AC，O为BC的中点，点E，D分别为边AB，AC上的点，且满足OE⊥OD，求证：OE=OD．  24. ( 15分 ) 如图，在平行四边形ABCD中，E是AD边上的中点，连接BE，并延长BE交CD的延长线于点F．证明：FD=AB．  25. ( 15分 ) 已知：如图，DE⊥AC，BF⊥AC，AD=BC，DE=BF，求证：AD∥BC 
答案解析部分一、单选题1.【答案】 A【解析】解：A、根据同底数幂相除底数不变指数相减a6÷a3＝a6-3=a3, 故本选项符合题意； B、a2•a4＝a6  ， 故本选项不符合题意；；C、3a2﹣a2＝2 a2  ， 故本选项不符合题意；D、（﹣ab2）3＝﹣a3b6  ， 故本选项不符合题意；．2.【答案】 C   【解析】解：A、 ，故本选项不合题意； B、（a2）3＝a6  ， 故本选项不合题意；C、a﹣1÷a﹣3＝a﹣1+3＝a2  ， 故本选项符合题意；D、（a+b）2＝a2+2ab+b2  ， 故本选项不合题意．3.【答案】 B   【解析】解：A、a2·a3=a5  ， 故A错误；
B、(a3)2=a6  ， 故B正确；
C、(3x)2=9x2  ， 故C错误；
D、2a与3b不是同类项，不能合并，故D错误.
4.【答案】 B   【解析】解：如图，连接BF， 在菱形ABCD中，∠BAC= ∠BAD= ×100°=50°，∵EF是AB的垂直平分线，∴AF=BF，∴∠FBA=∠FAB=50°，∵菱形ABCD的对边AD∥BC，∴∠ABC=180°-∠BAD=180°-100°=80°，∴∠CBF=∠ABC-∠ABF=80°-50°=30°，由菱形的对称性，∠CDF=∠CBF=30°．5.【答案】 A   【解析】解：A、 ，故此选项正确； B、9a3÷3a3＝3，故此选项错误；C、2a3+3a3＝5a3  ， 故此选项错误；D、（﹣a3）2＝a6  ， 故此选项错误.6.【答案】 D   【解析】已知等式整理得：x2+2ax+a2=x2-10x+b， 可得2a=-10，a2=b，解得：a=-5，b=25，7.【答案】 A   【解析】解:过A作AH⊥BC于H 1 ∵D是A B的中点∴AD=BD， BC∴DF= AH∵△DFE的面积为1， ，∴∵AB=CE∴AB=2 (负值舍去)，∴AC=4，8.【答案】 D   【解析】解： ，故A不符合题意； ，故B不符合题意； ，故C不符合题意； ，故D符合题意；9.【答案】 A   【解析】自左到右，依次为△ADB≌△ADE，△ACB≌△ACE，△DBC≌△DEC， 有3对，10.【答案】 C   【解析】∵ ∴ ∵EF垂直平分AB∴点A  ， B关于直线EF对称∴ ∴ ，二、填空题11.【答案】 3   【解析】解：∵25＜28＜36，
∴5＜ ＜6，
∴5-2＜-2＜6-2，
∴3＜-2＜4， ∴ 的整数部分是：3.12.【答案】 1   【解析】解：原式= . 13.【答案】    【解析】解：由题意作图，再作OP⊥BC， OP的长即为边心距，即OP=1，由△ABC是正三角形，∴∠ABC=60°，又∵OP平分∠ABC，则∠OBP=30°，∴OB=2OP，由勾股定理知：BP= = ，∴BC= ，即边长为 ，14.【答案】 10   【解析】在Rt△ABC中，AC=8m，BC=6m，
∴AB==10（m），
∴ 这位游泳爱好者在横跨河流的实际游泳距离为10m.
15.【答案】 8   【解析】解：作CD⊥x轴于D  ， 如图， 在△OAB和△DCB中， ∴△OAB≌△DCB（AAS），∴S△AOB＝S△CDB  ， ∴S△COD＝S△AOC＝4，∵S△COD＝ |k|，∴ |k|＝4，而k＞0，∴k＝8．16.【答案】    【解析】设AB的中点为E，连接OE、DE、OD， ∵∠AOB=90°，AB的中点为E，AB=6，∴OE=AE= AB=3，∵四边形ABCD是矩形，BC =3，∴AD=BC=3，∴DE= = ，∵OE+DE≥OD，∴O、E、D三点共线时OD有最大值OE+DE=3+ ，17.【答案】 65°   【解析】解：∵ 将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A'B'C，
∴ Rt△ABC≌△A'B'C，∠BCB'=90°
∴BC=B'C，∠ABC=∠CB'A'
∴∠CB'B=45°；
∴∠ABC=∠CB'A'=∠CB'B- ∠A'B'B=45°-20°=25°
∴∠A=90°-∠ABC=90°-25°=65°.
18.【答案】 或    【解析】解：∵∠AEF=∠B=∠C，且∠AME＞∠C， ∴∠AME＞∠AEF，∴AE≠AM；当AE=EM时，∵∠AEB=∠MAE+∠C，∠EMC=∠MAE+∠AEM=∠MAE+∠B=∠MAE+∠C∴∠AEB=∠EMC又∵∠B=∠C∴△ABE≌△ECM，∴CE=AB=5，∴BE=BC-EC=6-5=1，当AM=EM时，则∠MAE=∠MEA，∴∠MAE+∠BAE=∠MEA+∠CEM，即∠CAB=∠CEA，又∵∠C=∠C，∴△CAE∽△CBA，∴ ∴ ∴ ．19.【答案】    【解析】 = = 20.【答案】 6   【解析】∵（a-b）2=4，ab= ， ∴（a-b）2=a2+b2-2ab，=a2+b2-1=4，∴a2+b2=5，∴（a+b）2=a2+b2+2ab=5+1=6．三、计算题21.【答案】 解：原式=   =    【解析】原式利用立方根的定义、去括号的法则、二次根式的性质、绝对值的代数意义计算即可求解.四、作图题22.【答案】 （1）解：如图，直线PQ即为所求作.
（2）解：结论：BC=PA+PC. 理由：∵PQ垂直平分线段AB，∴PA=PB，∴PB+PC=PA+PC=BC.【解析】（1）利用线段垂直平分线的作法，作出线段AB的垂直平分线.（2）利用线段垂直平分线的性质，可证得AP=PB，再根据BC=PB+PC，可证得结论.五、解答题23.【答案】 证明：  如图，连接AO，∵∠BAC=90°，AB=AC，O为BC的中点，∴AO=BO，∠OAD=∠B=45°，∵AO⊥BO，OE⊥OD，∴∠AOE+∠BOE=∠AOE+∠AOD=90°，在△AOD和△BOE中  ∴△AOD≌△BOE，∴OE=OD．【解析】连接AO，证明△BEO≌△ADO即可．24.【答案】 证明：∵四边形ABCD是平行四边形，  ∴AB∥CD，∴∠ABE=∠F，∵E是AD边上的中点，∴AE=DE，在△ABE和△DFE中，  ，∴△ABE≌△DFE（AAS），∴FD=AB【解析】由在平行四边形ABCD中，E是AD边上的中点，易证得△ABE≌△DFE（AAS），继而证得FD=AB．25.【答案】 证明：∵DE⊥AC，BF⊥AC，  ∴∠AED=∠CFB=90°，∵AD=BC，DE=BF，∴Rt△AED≌Rt△CFB（HL），∴∠DAE=∠BCF，∴AD∥BC．【解析】利用“HL”证出  ， 得出  ， 利用内错角相等，证出AD//BC。