初中数学人教版九年级上册24.1.2 垂直于弦的直径课堂教学课件ppt

这是一份初中数学人教版九年级上册24.1.2 垂直于弦的直径课堂教学课件ppt，共18页。PPT课件主要包含了温故知新，探究活动一，探究活动二，垂径定理，探究活动三，口算并说说理由，在Rt△AOE中，你会了吗，探究活动四，h+dr等内容，欢迎下载使用。

1、我们所学的圆是不是轴对称图形呢？
圆是轴对称图形，经过圆心的每一条直线都是它们的对称轴
2、我们所学的圆是不是中心对称图形呢？
圆是中心对称图形，圆心是对称中心
3、填空： （1）根据圆的定义，“圆”指的是“ ”，是 线，而不是“圆面”。（2）圆心和半径是确定一个圆的两个必需条件，圆心决定圆的 ，半径决定圆的 ，二者缺一不可。（3）同一个圆的半径 。
　 把一个圆沿着它的任意一条直径所在的直线对折，两侧半圆会有什么关系？重复做几次，你发现了什么？由此你能得到什么结论？
可以发现： 圆是轴对称图形，任何一条直径所在直线（或者任何经过圆心的直线）都是它的对称轴，所以两侧半圆折叠后完全重合. 　
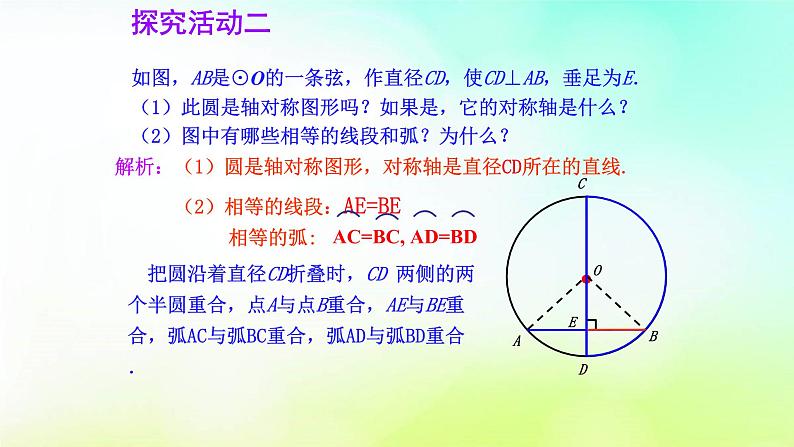
如图，AB是⊙O的一条弦，作直径CD，使CD⊥AB，垂足为E．（1）此圆是轴对称图形吗？如果是，它的对称轴是什么？（2）图中有哪些相等的线段和弧？为什么？
解析：（1）圆是轴对称图形，对称轴是直径CD所在的直线.
（2）相等的线段：AE=BE
把圆沿着直径CD折叠时，CD 两侧的两个半圆重合，点A与点B重合，AE与BE重合，弧AC与弧BC重合，弧AD与弧BD重合．
AC=BC, AD=BD
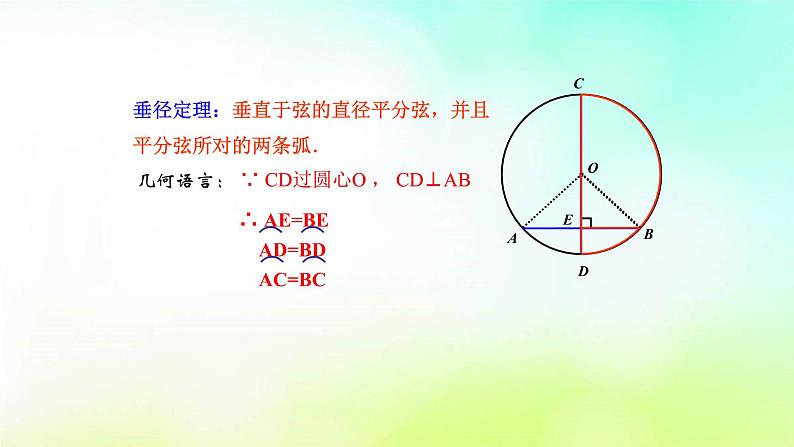
几何语言： ∵ CD过圆心O ， CD⊥AB
∴ AE=BE AD=BD AC=BC
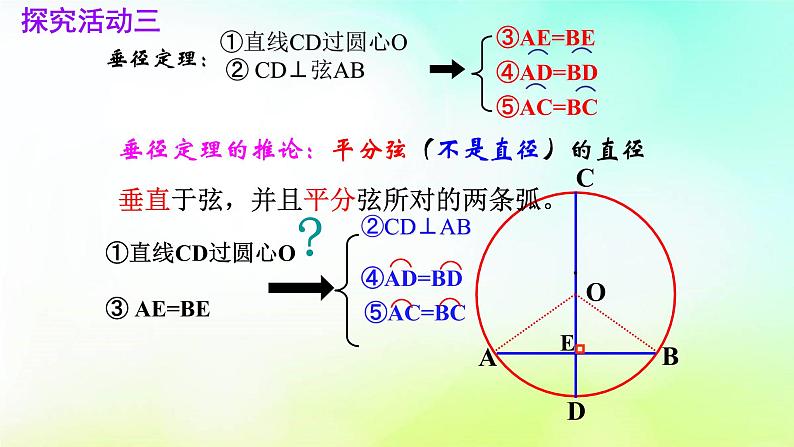
①直线CD过圆心O ② CD⊥弦AB
①直线CD过圆心O③ AE=BE
垂径定理的推论：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧。
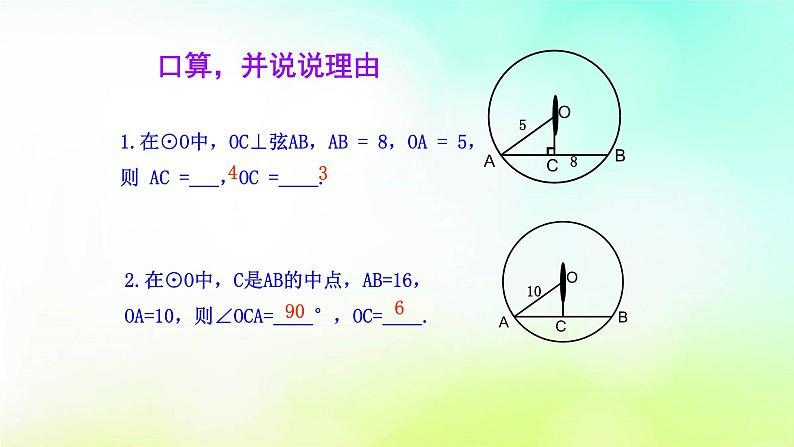
1.在⊙O中，OC⊥弦AB，AB = 8，OA = 5，则 AC = ，OC = .
2.在⊙O中，C是AB的中点，AB=16，OA=10，则∠OCA= °，OC= .
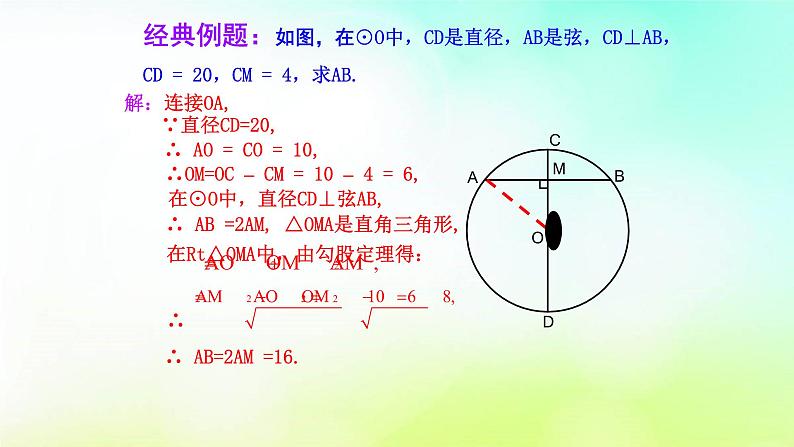
在⊙O中，直径CD⊥弦AB,
∴ AB =2AM, △OMA是直角三角形,
∴ AO = CO = 10,
∴OM=OC – CM = 10 – 4 = 6,
在Rt△OMA中，由勾股定理得：
∴ AB=2AM =16.
经典例题：如图，在⊙O中，CD是直径，AB是弦，CD⊥AB，CD = 20，CM = 4，求AB.
如图，在⊙O 中，弦AB的长为8cm，圆心O 到AB 的距离为3cm，求⊙O 的半径．
答：⊙O 的半径为5cm.
常见辅助线：连接半径、作弦心距；技巧：构造直角三角形，设未知数，由勾股定理列方程。
四个量：半径 r 、弦长a 、弦心距d、弓形的高h
解得：R≈27.9（m）
在Rt△OAD中，由勾股定理，得
即 R2=18.72+（R－7.2）2
∴赵州桥的主桥拱半径约为27.9m.
OA2=AD2+OD2
AB=37.4，CD=7.2，
OD=OC－CD=R－7.2
一、判断下列说法的正误
①平分弧的直径必平分弧所对的弦
　②平分弦的直线必垂直弦
③垂直于弦的直径平分这条弦
④平分弦的直径垂直于这条弦
⑤弦的垂直平分线是圆的直径
⑥平分弦所对的一条弧的直径必垂直这条弦
⑦在圆中，如果一条直线经过圆心且平分弦，　　必平分此弦所对的弧
⑧分别过弦的三等分点作弦的垂线，将弦所对　　的两条弧分别三等分
3．半径为2cm的圆中，过半径中点且 垂直于这条半径的弦长是 。
1．半径为4cm的⊙O中，弦AB=4cm, 那么圆心O到弦AB的距离是 。
2． ⊙O的直径为10cm，圆心O到弦AB的 距离为3cm，则弦AB的长是 。
4、⊙O的半径为10cm，弦AB∥CD， AB=16，CD=12，则AB、CD间的 距离是___ .
1、已知：如图，在以O为圆心的两个同心圆中，大圆的弦AB交小圆于C，D两点。求证：AC＝BD。
证明：过O作OE⊥AB，垂足为E， 则AE＝BE，CE＝DE。 AE－CE＝BE－DE。 所以，AC＝BD
2．如图，在⊙O中，AB、AC为互相垂直且相等的两条弦，OD⊥AB于D，OE⊥AC于E，求证四边形ADOE是正方形．
∴四边形ADOE为矩形，
∴ 四边形ADOE为正方形.
推论：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．
有关弦的问题，常常连接半径、作弦心距，这是两条非常重要的辅助线．圆心到弦的距离、半径、弦长的一半构成直角三角形，便将问题转化为直角三角形的勾股定理问题．