2022年高考数学(理数)一轮考点精选练习32《空间几何体及其体积、表面积》(含详解)

这是一份2022年高考数学(理数)一轮考点精选练习32《空间几何体及其体积、表面积》(含详解)，共7页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。

一、选择题
已知A，B是球O的球面上两点，∠AOB=90°，C为该球面上的动点.若三棱锥O-ABC体积的最大值为36，则球O的表面积为( )
A.36π B.64π C.144π D.256π
如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的正视图和侧视图，且该几何体的体积为eq \f(8,3)，则该几何体的俯视图可以是( )

一个几何体的三视图如图所示，其中正视图是一个正三角形，则这个几何体的外接球的表面积为( )
A.eq \f(16π,3) B.eq \f(8π,3) C.4eq \r(3)π D.eq \r(3)π
如图，△A′B′O′是利用斜二测画法画出的△ABO的直观图，已知A′B′∥y′轴，O′B′=4，且△ABO的面积为16，过A′作A′C′⊥x′轴，则A′C′的长为( )
A.2eq \r(2) B.eq \r(2) C.16eq \r(2) D.1
如图，在正四棱柱ABCD－A1B1C1D1中，点P是平面A1B1C1D1内一点，则三棱锥P－BCD的正(主)视图与侧(左)视图的面积之比为( )
A.1∶1 B.2∶1 C.2∶3 D.3∶2
如图，网格纸上小正方形的边长为1，图中粗线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为( )
A.2eq \r(3) B.3 C.eq \r(6) D.eq \r(5)
已知在长方体ABCD­A1B1C1D1中，底面是边长为2的正方形，高为4，则点A1到截面AB1D1的距离是( )
A.eq \f(8,3) B.eq \f(3,8) C.eq \f(4,3) D.eq \f(3,4)
一个几何体的三视图如图所示(其中正视图的弧线为四分之一圆周)，则该几何体的表面积为( )
A.72＋6π B.72＋4π C.48＋6π D.48＋4π
圆环内圆半径为4，外圆半径为5，则圆环绕其对称轴旋转一周形成的几何体的体积为( )
A.eq \f(244π,3) B.eq \f(500π,3) C.eq \f(200π,3) D.eq \f(256π,3)
“牟合方盖”(如图1)是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体.它由完全相同的四个曲面构成，相对的两个曲面在同一个圆柱的侧面上，好似两个扣合(牟合)在一起的方形伞(方盖).其直观图如图2所示，图中四边形是为体现其直观性所作的辅助线，其实际直观图中四边形不存在，当其正视图和侧视图完全相同时，它的正视图和俯视图分别可能是( )
A.a，b B.a，c C.c，b D.b，d
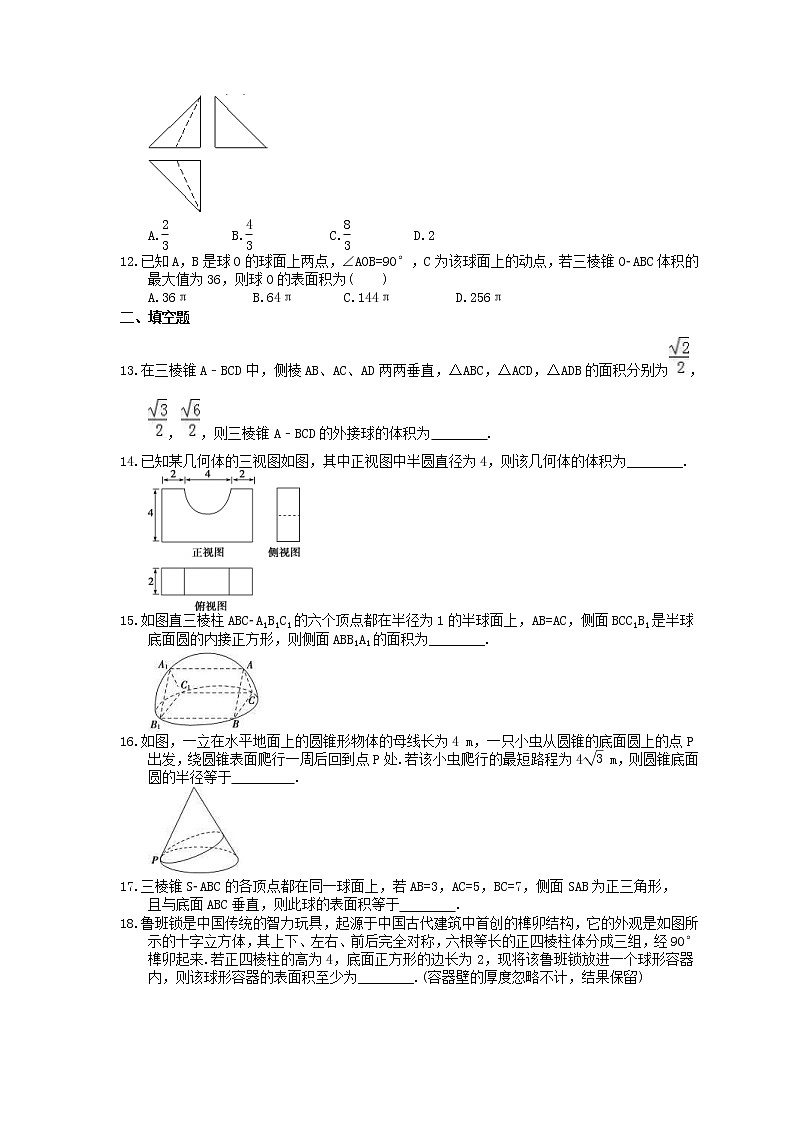
如图是一个四面体的三视图，这三个视图均是腰长为2的等腰直角三角形，正视图和俯视图中的虚线是三角形的中线，则该四面体的体积为( )
A.eq \f(2,3) B.eq \f(4,3) C.eq \f(8,3) D.2
已知A，B是球O的球面上两点，∠AOB=90°，C为该球面上的动点，若三棱锥O­ABC体积的最大值为36，则球O的表面积为( )
A.36π B.64π C.144π D.256π
二、填空题
在三棱锥A﹣BCD中，侧棱AB、AC、AD两两垂直，△ABC，△ACD，△ADB的面积分别为，，，则三棱锥A﹣BCD的外接球的体积为 .
已知某几何体的三视图如图，其中正视图中半圆直径为4，则该几何体的体积为________.
如图直三棱柱ABC­A1B1C1的六个顶点都在半径为1的半球面上，AB=AC，侧面BCC1B1是半球底面圆的内接正方形，则侧面ABB1A1的面积为________.
如图，一立在水平地面上的圆锥形物体的母线长为4 m，一只小虫从圆锥的底面圆上的点P出发，绕圆锥表面爬行一周后回到点P处.若该小虫爬行的最短路程为4eq \r(3) m，则圆锥底面圆的半径等于 .
三棱锥S­ABC的各顶点都在同一球面上，若AB=3，AC=5，BC=7，侧面SAB为正三角形，
且与底面ABC垂直，则此球的表面积等于 .
鲁班锁是中国传统的智力玩具，起源于中国古代建筑中首创的榫卯结构，它的外观是如图所示的十字立方体，其上下、左右、前后完全对称，六根等长的正四棱柱体分成三组，经90°榫卯起来.若正四棱柱的高为4，底面正方形的边长为2，现将该鲁班锁放进一个球形容器内，则该球形容器的表面积至少为________.(容器壁的厚度忽略不计，结果保留)
\s 0 答案解析
答案为：C；
解析：∵S△OAB是定值，且VO-ABC=VC-OAB，
∴当OC⊥平面OAB时，VC-OAB最大，即VO-ABC最大.
设球O的半径为R，则(VO-ABC)max=eq \f(1,3)×eq \f(1,2)R2×R=eq \f(1,6)R3=36，
∴R=6，∴球O的表面积S=4πR2=4π×62=144π.
答案为：C.
解析：若俯视图为选项C中的图形，则该几何体为正方体截去一部分后的四棱锥P­ABCD，如图所示，该四棱锥的体积V=eq \f(1,3)×(2×2)×2=eq \f(8,3)，符合题意.
若俯视图为其他选项中的图形，则根据三视图易判断对应的几何体不存在，故选C.
答案为：A
解析：由三视图可知，该几何体为一个三棱锥，令其为三棱锥A－BCD，
由俯视图可知，底面BCD是一个等腰直角三角形，∠BCD为直角.
平面ABD⊥平面BCD，易知外接球的球心O为△ABD的中心，
则球O的半径R=eq \f(2 \r(3),3)，外接球的表面积等于4πR2=4π×eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2 \r(3),3)))2=eq \f(16π,3).
答案为：A；
解析：因为A′B′∥y′轴，所以△ABO中，AB⊥OB.
又因为△ABO的面积为16，所以eq \f(1,2)AB·OB=16.
因为OB=O′B′=4，所以AB=8，所以A′B′=4.
因为A′C′⊥O′B′于C′，所以B′C′=A′C′，
所以A′C′=4·sin45°=2eq \r(2)，故选A.
答案为：A
解析：根据题意，三棱锥P－BCD的正视图是三角形，且底边为正四棱柱的底面边长，
高为正四棱柱的高；侧视图是三角形，且底边为正四棱柱的底面边长，
高为正四棱柱的高.故三棱锥P－BCD的正(主)视图与侧(左)视图的面积之比为1∶1.
答案为：B.
解析：根据三视图，利用棱长为2的正方体分析知，该多面体是一个三棱锥，
即三棱锥A1­MNP，如图所示，其中M，N，P是棱长为2的正方体相应棱的中点，
可得棱A1M最长，A1M=eq \r(22＋22＋12)=3，故最长的棱的长度为3，故选B.
答案为：C；
解析：设点A1到截面AB1D1的距离是h，由VA1­AB1D1=VA­A1B1D1，
可得eq \f(1,3)S△AB1D1·h=eq \f(1,3)S△A1B1D1·AA1，即eq \f(1,3)×eq \f(1,2)×2×2×4=eq \f(1,3)×eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)×2\r(2)×3\r(2)))h，解得h=eq \f(4,3).
答案为：A.
解析：由三视图知，该几何体由一个正方体的eq \f(3,4)部分与一个圆柱的eq \f(1,4)部分组合而成(如图所示)，其表面积为16×2＋(16－4＋π)×2＋4×(2＋2＋π)=72＋6π.
答案为：A；
解析：该旋转体是大球体中挖掉一个小球体，该旋转体体积为V=eq \f(4π,3)×53－eq \f(4π,3)×43=eq \f(244π,3).
答案为：A；
解析：当正视图和侧视图完全相同时，“牟合方盖”相对的两个曲面正对前方，正视图为一个圆，俯视图为一个正方形，且两条对角线为实线，故选A.
答案为：A
解析：由三视图可知，此四面体如图所示，其高为2，底面三角形的一边长为1，
对应的高为2，所以其体积V=eq \f(1,3)×eq \f(1,2)×2×1×2=eq \f(2,3).故选A.
答案为：C；
解析：如图所示，当点C位于垂直于面AOB的直径端点时，三棱锥O­ABC的体积最大，
设球O的半径为R，此时VO­ABC=VC­AOB=eq \f(1,3)×eq \f(1,2)R2×R=eq \f(1,6)R3=36，故R=6，
则球O的表面积为S=4πR2=144π.
答案为：π
解析：三棱锥A﹣BCD中，侧棱AB、AC、AD两两垂直，补成长方体，两者的外接球是同一个，
长方体的对角线就是球的直径，设长方体的三度为a，b，c，
则由题意得：ab=，ac=，bc=，解得：a=，b=，c=1，
所以球的直径为： =所以球的半径为，
所以三棱锥A﹣BCD的外接球的体积为=π
答案为：64－4π
解析：由三视图可知该几何体为一个长方体挖掉半个圆柱，
所以其体积为2×4×8－eq \f(1,2)×π×22×2=64－4π.
答案为：eq \r(2).
解析：由题意知，球心在侧面BCC1B1的中心O上，BC为截面圆的直径，
所以∠BAC=90°，△ABC的外接圆圆心N是BC的中点，同理△A1B1C1的外心M是B1C1的中点.设正方形BCC1B1的边长为x.在Rt△OMC1中，OM=eq \f(x,2)，MC1=eq \f(x,2)，OC1=R=1(R为球的半径)，
所以(eq \f(x,2))2＋(eq \f(x,2))2=1，即x=eq \r(2)，则AB=AC=1，所以S矩形ABB1A1=eq \r(2)×1=eq \r(2).
答案为：eq \f(4,3)m.
解析：把圆锥侧面沿过点P的母线展开成如图所示的扇形，
由题意OP=4，PP′=4eq \r(3)，则cs∠POP′=eq \f(42＋42－4\r(3)2,2×4×4)=－eq \f(1,2)，
所以∠POP′=eq \f(2π,3).设底面圆的半径为r，则2πr=eq \f(2π,3)×4，所以r=eq \f(4,3).
答案为：eq \f(205π,3).
解析：设△ABC外接圆的圆心为O1，△SAB外接圆的圆心为O2，过O1，O2分别作平面ABC，平面SAB的垂线交于点O，则O为球心.
在△ABC中，cs∠BAC=eq \f(52＋32－72,2×3×5)=－eq \f(1,2)，∴∠BAC=120°，
设圆O1的半径为r1，根据正弦定理，得2r1=eq \f(BC,sin∠BAC)=eq \f(14\r(3),3)，∴r1=eq \f(7\r(3),3).
△SAB外接圆的圆心O2为正三角形SAB的中心，连接SO2交AB于点D，
则O2D=eq \f(1,3)SD=eq \f(\r(3),2)，且O2D=OO1=eq \f(\r(3),2).
设外接球的半径为R，连接O1A，则R2=O1A2＋OOeq \\al(2,1)=eq \f(49,3)＋eq \f(3,4)=eq \f(205,12)，
∴此球的表面积S=4πR2=eq \f(205π,3).
答案为：36π
解析：该球形容器最小时，十字立方体与球内接，
此时球直径2R等于由两个正四棱柱组合而成的几何体的对角线，即2R=eq \r(42＋42＋22)=6，
球形容器的表面积为4πR2=36π.