第二讲.空间向量及其在立体几何中的应用练习题

第二讲.空间向量及其在立体几何中的应用

一．空间向量与空间角的关系

1.两条异面直线所成角的求法

设两条异面直线a，b的方向向量分别为a，b，其夹角为θ，则cosφ＝|cosθ|＝(其中φ为异面直线a，b所成的角)．

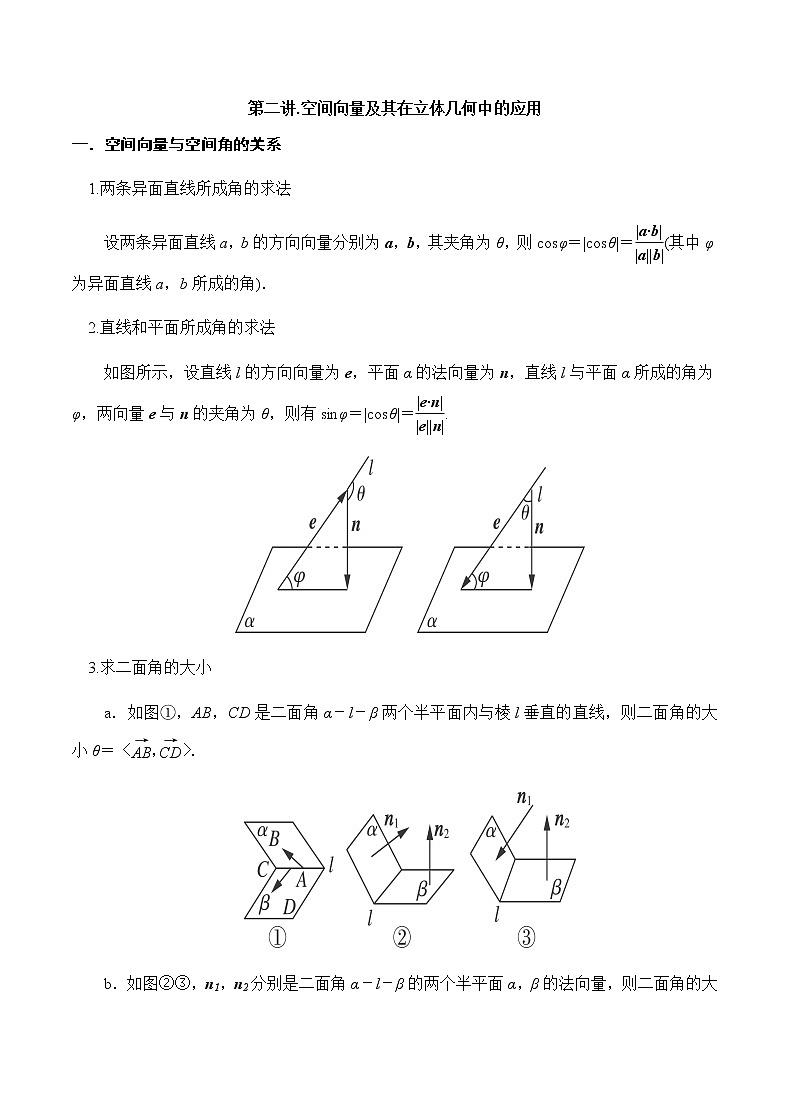
2.直线和平面所成角的求法

如图所示，设直线l的方向向量为e，平面α的法向量为n，直线l与平面α所成的角为φ，两向量e与n的夹角为θ，则有sinφ＝|cosθ|＝.

3.求二面角的大小

a．如图①，AB，CD是二面角α－l－β两个半平面内与棱l垂直的直线，则二面角的大小θ＝〈，〉．

b．如图②③，n1，n2分别是二面角α－l－β的两个半平面α，β的法向量，则二面角的大小θ满足cosθ＝cos〈n1，n2〉或－cos〈n1，n2〉．

4．点到平面的距离的求法

如图，设AB为平面α的一条斜线段，n为平面α的法向量，则点B到平面α的距离d＝.

二．空间向量与空间线线，线面，面面的位置

1.用向量方法研究两直线间的位置关系

设直线l1、l2的方向向量分别为a、b.

(1) l1∥l2或l1与l2重合⇔a∥b⇔存在实数t，使a＝tb.

(2) l1⊥l2⇔a⊥b⇔a·b＝0.

2.用向量方法研究直线与平面的位置关系

设直线l的方向向量为a，平面α的法向量为n，v1、v2是与α平行的两个不共线向量．

(1)l∥α或l⊂α⇔存在两个实数λ、μ，使a＝λv1＋μv2⇔a·n＝0.

(2)l⊥α⇔a∥n⇔存在实数t，使a＝tn.

3.用向量方法研究两个平面的位置关系

设平面α、β的法向量分别为n1、n2.

(1)α∥β或α与β重合⇔ n1∥n2⇔存在实数t，使n1＝t n2.

(2)α⊥β⇔ n1⊥n2⇔ n1·n2＝0.

若v1、v2是与α平行的两个不共线向量，n是平面β的法向量．

则①α∥β或α与β重合⇔ v1∥β且v2∥β⇔存在实数λ、μ，对β内任一向量a，有a＝λv1＋μv2.

②

三．例题讲解

 题型一 用向量证明平行

例1.在正方体ABCD－A1B1C1D1中，M、N分别是C1C、B1C1的中点．求证：MN∥平面A1BD.

证明：方法1：如图所示，以D为原点，DA、DC、DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系，设正方体的棱长为1，则可求得M，N，A1(1,0,1)，B(1,1,0)，于是＝，设平面A1BD的法向量是n＝(x，y，z)．则n·＝0，且n·＝0，∴，

取x＝1，得y＝－1，z＝－1.∴n＝(1，－1，－1)．

又·n＝·(1，－1，－1)＝0，

∴⊥n，又∵MN⊄平面A1BD，∴MN∥平面A1BD.

方法2：∵＝－＝－＝(－)＝，

∴∥，又∵MN⊄平面A1BD.

∴MN∥平面A1BD.

点评：(1)证明直线l1∥l2时，分别取l1、l2的一个方向向量a、b，则a∥b⇔存在实数k，使a＝kb或利用其坐标＝＝(其中a＝(a1，a2，a3)，b＝(b1，b2，b3))．

(2)证明直线l∥平面α时，

①可取直线l的方向向量a与平面α的法向量n，证明a·n＝0；

②可在平面α内取基向量{e1，e2}，证明直线l的方向向量a＝λ1e1＋λ2e2，然后说明l不在平面α内即可；

③在平面α内找两点A、B，证明直线l的方向向量n∥.

(3)证明平面α∥平面β时，设α、β的法向量分别为a、b，则只须证明a∥b.

 题型二 用向量证明线面垂直

[例2]　在棱长为1的正方体ABCD－A1B1C1D1中，E、F分别为棱AB和BC的中点，试在棱B1B上找一点M，使得D1M⊥平面EFB1.

证明：分别以DA、DC、DD1所在直线为x轴、y轴、z轴建立空间直角坐标系D－xyz，

则A(1,0,0)，B1(1,1,1)，C(0,1,0)，D1(0,0,1)，E，M(1,1，m)．∴＝(－1,1,0)，

又E、F分别为AB、BC的中点，

∴＝＝.

又∵＝，＝(1,1，m－1)，

∵D1M⊥平面FEB1，∴D1M⊥EF且D1M⊥B1E.

即·＝0，且·＝0.

∴，∴m＝.

故取B1B的中点M就能满足D1M⊥平面EFB1.

点评：①证明直线 l1与l2垂直时，取l1、l2的方向向量a、b，证明a·b＝0.

②证明直线l与平面α垂直时，取α的法向量n，l的方向向量a，证明a∥n.

或取平面α内的两相交直线的方向向量a、b与直线l的方向向量e，证明a·e＝0，b·e＝0.

③证明平面α与β垂直时，取α、β的法向量n1、n2，证明n1·n2＝0.或取一个平面α的法向量n，在另一个平面β内取基向量{e1，e2}，证明n＝λe1＋μe2.

题型三 用向量法证明面面垂直与面面平行

[例3]　已知正方体ABCD－A1B1C1D1的棱长为2，E、F、G分别是BB1、DD1、DC的中点，求证：

(1)平面ADE∥平面B1C1F；

(2)平面ADE⊥平面A1D1G；

(3)在AE上求一点M，使得A1M⊥平面DAE.

解析：以D为原点，、、为正交基底建立空间直角坐标系O－xyz，则D(0,0,0)，D1(0,0,2)，A(2,0,0)，A1(2,0,2)，E(2,2,1)，F(0,0,1)，G(0,1,0)，B1(2,2,2)，C1(0,2,2)．

(1)设n1＝(x1，y1，z1)，n2＝(x2，y2，z2)分别是平面ADE、平面B1C1F的法向量，则n1⊥，n1⊥.

∴，∴，

取y1＝1，z1＝－2，∴n1＝(0,1，－2)．

同理可求n2＝(0,1，－2)．

∵n1∥n2，∴平面ADE∥平面B1C1F.

(2)∵·＝(2,0,0)·(0,1，－2)＝0，∴⊥.

∵·＝(0,2,1)·(0,1，－2)＝0，∴⊥.

∵、不共线，∴D1G⊥平面ADE.

又∵D1G⊂平面A1D1G，∴平面ADE⊥平面A1D1G.

(3)由于点M在AE上，所以可设＝λ·＝λ·(0,2,1)＝(0,2λ，λ)，

∴M(2,2λ，λ)，＝(0,2λ，λ－2)．

要使A1M⊥平面DAE，只需A1M⊥AE，

∴·＝(0,2λ，λ－2)·(0,2,1)＝5λ－2＝0，

∴λ＝.故当AM＝AE时，A1M⊥平面DAE.

跟踪练习1

已知四棱锥P－ABCD的底面是直角梯形，∠ABC＝∠BCD＝90°，AB＝BC＝PB＝PC＝2CD，侧面PBC⊥底面ABCD.

(1)证明：PA⊥BD；

(2)证明：平面PAD⊥平面PAB.

证明：(1)取BC的中点O，

∵侧面PBC⊥底面ABCD，△PBC为等边三角形，

∴PO⊥底面ABCD.

以O为坐标原点，以BC所在直线为x轴，过点O与AB平行的直线为y轴，建立如图所示空间直角坐标系．

不妨设CD＝1，则AB＝BC＝2，PO＝.

∴A(1，－2,0)，B(1,0,0)，D(－1，－1,0)，P(0,0，)．

∴＝(－2，－1,0)，＝(1，－2，－)．

∵·＝0，∴⊥，∴PA⊥BD.

(2)取PA的中点M，连结DM，则M.

∵＝，＝(1,0，－)，

∴·＝0，∴⊥，即DM⊥PA.

又·＝0，∴⊥，即DM⊥PB.

∴DM⊥平面PAB，∴平面PAD⊥平面PAB.

点评：线线垂直即直线的方向向量垂直；线面垂直即直线的方向向量与平面的法向量平行；面面垂直即二平面的法向量垂直.

题型四 用向量法求异面直线所成的角

[例4]　(2010·衡水市模考)正四棱锥P－ABCD的所有棱长相等，E为PC的中点，那么异面直线BE与PA所成角的余弦值等于（      ）

A．          B．          C．         D．

解析：以，，为基向量，则＝(＋)＝(＋－)，由条件知，||＝||＝||＝1，·＝，·＝，·＝0，

∴·＝(·＋||2－·)＝＝，

||2＝(||2＋||2＋||2－2·－2·＋2·)＝(1＋1＋1－0－1＋1)＝，

∴||＝，∴cos〈，〉＝＝＝，故选D.

点评：①由几何体的特殊性，在求||时，可直接在正三角形PBC中得||＝BE＝.

②可连结AC，取AC中点O，则EO∥PA，∴∠BEO为所求角，通过解△BEO求得.

题型五 线面角

[例5]　如图，已知点P在正方体ABCD－A′B′C′D′的对角线BD′上，∠PDA＝60°.

(1)求DP与CC′所成角的大小；

(2)求DP与平面AA′D′D所成角的大小．

解析：如图，以D为原点，DA为单位长建立空间直角坐标系D－xyz.

则＝(1,0,0)，＝(0,0,1)，连结BD，B′D′.

在平面BB′D′D中，延长DP交B′D′于H.

设＝(m，m,1)(m>0)，由已知〈，〉＝60°，

由·＝||||cos〈，〉

可得2m＝.

解得m＝，所以＝.

(1)因为cos〈，〉＝＝，

所以〈，〉＝45°，

即DP与CC′所成的角为45°.

(2)平面AA′D′D的一个法向量是＝(0,1,0)．

因为cos〈，〉＝＝，

跟踪练习2

(2010·湖南理)如图所示，在正方体ABCD－A1B1C1D1中，E是棱DD1的中点．

(1)求直线BE和平面ABB1A1所成的角的正弦值；

(2)在棱C1D1上是否存在一点F，使B1F∥平面A1BE？证明你的结论．

解析：设正方体的棱长为1，建立如图所示的空间直角坐标系.

(1)依题意，得B(1,0,0)，E(0,1，)，A(0,0,0)，D(0,1,0)，

所以＝(－1,1，)，＝(0,1,0)．

在正方体ABCD－A1B1C1D1中，因为AD⊥平面ABB1A1，所以是平面ABB1A1的一个法向量，设直线BE与平面ABB1A1所成的角为θ，则

sinθ＝＝＝.

即直线BE与平面ABB1A1所成的角的正弦值为.

(2)依题意，得A1(0,0,1)，＝(－1,0,1), ＝(－1,1，)．

设n＝(x，y，z)是平面A1BE得一个法向量，则由n·＝0，n·＝0，得

所以x＝z，y＝z.取z＝2，得n＝(2,1,2)．

设F是棱C1D1上的点，则F(t,1,1)(0≤t≤1)．

又B1(1,0,1)，所以＝(t－1,1,0)，而B1F⊄平面A1BE，于是B1F∥平面A1BE⇔·n＝0⇔(t－1,1,0)·(2,1,2)＝0⇔2(t－1)＋1＝0⇔t＝⇔F为C1D1的中点．

这说明在棱C1D1上存在一点F(F为C1D1的中点)，使B1F∥平面A1BE.

题型六 二面角

[例6]　(2010·陕西理)如图，在四棱锥P－ABCD中，底面ABCD是矩形，PA⊥平面ABCD，AP＝AB＝2，BC＝2，E，F分别是AD，PC的中点．

(1)证明：PC⊥平面BEF.

(2)求平面BEF与平面BAP夹角的大小．

解析： (1)如图，以A为坐标原点AB，AD，AP所在直线分别为x，y，z轴建立空间直角坐标系，

∵AP＝AB＝2，BC＝AD＝2，四边形ABCD是矩形．

∴A，B，C，D，P的坐标为A(0,0,0)，B(2,0,0)，C(2,2，0)，

D(0,2，0)，P(0,0，，2)，

又E，F分别是AD，PC的中点，

∴E(0，，0)，F(1，，1)，

∴＝(2,2，－2)，＝(－1，，1)＝(1,0,1)，

∴·＝－2＋4－2＝0，·＝2＋0－2＝0，

∴⊥，⊥，

∴PC⊥BF，PC⊥EF，BF∩EF＝F，

∴PC⊥平面BEF.

(2)由(1)知平面BEF的法向量n1＝＝(2,2，－2)，

平面BAP的法向量n2＝＝(0,2，0)，∴n1·n2＝8，

设平面BEF与平面BAP的夹角为θ，

解法2：(1)连接PE，EC，

在Rt△PAE和Rt△CDE中，PA＝AB＝CD，AE＝DE，

∴PE＝CE，即△PEC是等腰三角形，

又F是PC的中点，∴EF⊥PC，

又BP＝＝2＝BC，F是PC的中点，

∴BF⊥PC，

又BF∩EF＝F，∴PC⊥平面BEF.

(2)∵PA⊥平面ABCD，∴PA⊥BC，

又ABCD是矩形，∴AB⊥BC，∴BC⊥平面BAP，BC⊥PB，

又由(1)知PC⊥平面BEF，∴直线PC与BC的夹角即为平面BEF与平面BAP的夹角，

在△PBC中，PB＝BC，∠PBC＝90°，∴∠PCB＝45°.

所以平面BEF与平面BAP的夹角为45°.