2018年秋人教版八年级数学上册第十三章 轴对称 检测卷

第十三章检测卷

时间：120分钟　　　　　满分：120分

一、选择题(本大题共6小题，每小题3分，共18分．每小题只有一个正确选项)

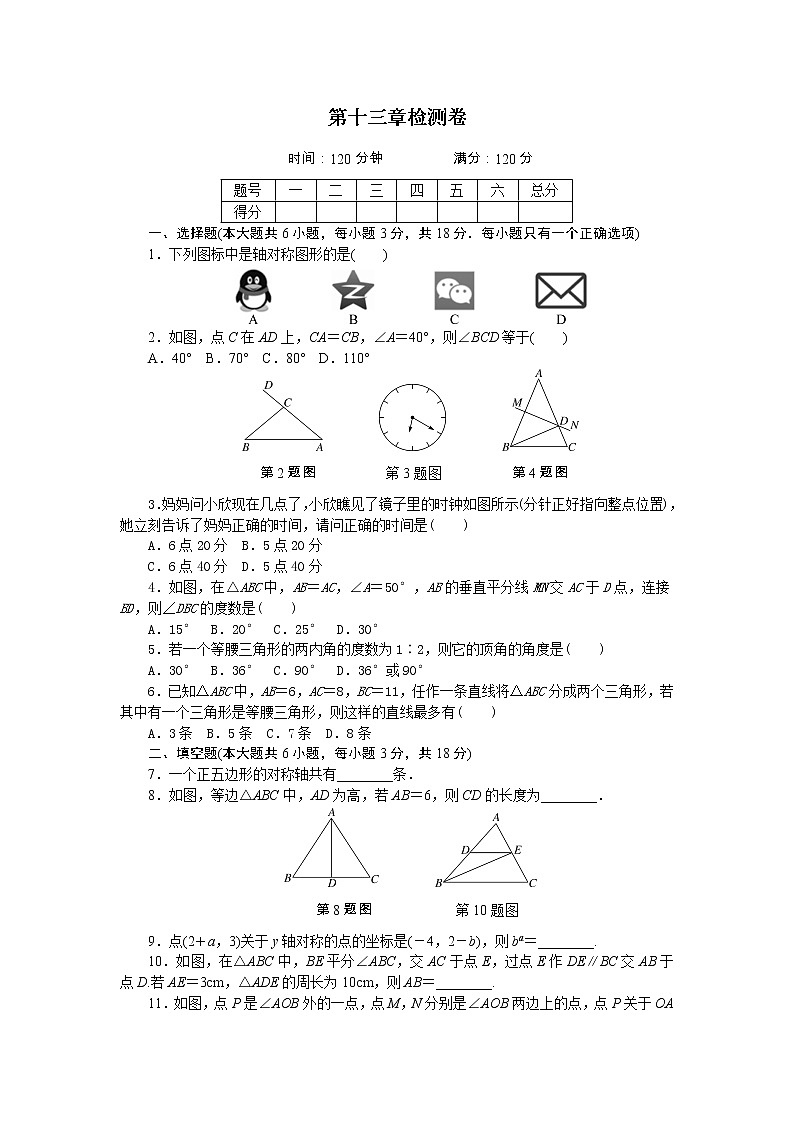
1．下列图标中是轴对称图形的是(　　)

2．如图，点C在AD上，CA＝CB，∠A＝40°，则∠BCD等于(　　)

A．40°  B．70°  C．80°  D．110°

第2题图          第3题图          第4题图

3．妈妈问小欣现在几点了，小欣瞧见了镜子里的时钟如图所示(分针正好指向整点位置)，她立刻告诉了妈妈正确的时间，请问正确的时间是(　　)

A．6点20分  B．5点20分

C．6点40分  D．5点40分

4．如图，在△ABC中，AB＝AC，∠A＝50°，AB的垂直平分线MN交AC于D点，连接BD，则∠DBC的度数是(　　)

A．15°  B．20°  C．25°  D．30°

5．若一个等腰三角形的两内角的度数为1∶2，则它的顶角的角度是(　　)

A．30°  B．36°  C．90°  D．36°或90°

6．已知△ABC中，AB＝6，AC＝8，BC＝11，任作一条直线将△ABC分成两个三角形，若其中有一个三角形是等腰三角形，则这样的直线最多有(　　)

A．3条  B．5条  C．7条  D．8条

二、填空题(本大题共6小题，每小题3分，共18分)

7．一个正五边形的对称轴共有________条．

8．如图，等边△ABC中，AD为高，若AB＝6，则CD的长度为________．

第8题图            第10题图

9．点(2＋a，3)关于y轴对称的点的坐标是(－4，2－b)，则ba＝________.

10．如图，在△ABC中，BE平分∠ABC，交AC于点E，过点E作DE∥BC交AB于点D.若AE＝3cm，△ADE的周长为10cm，则AB＝________.

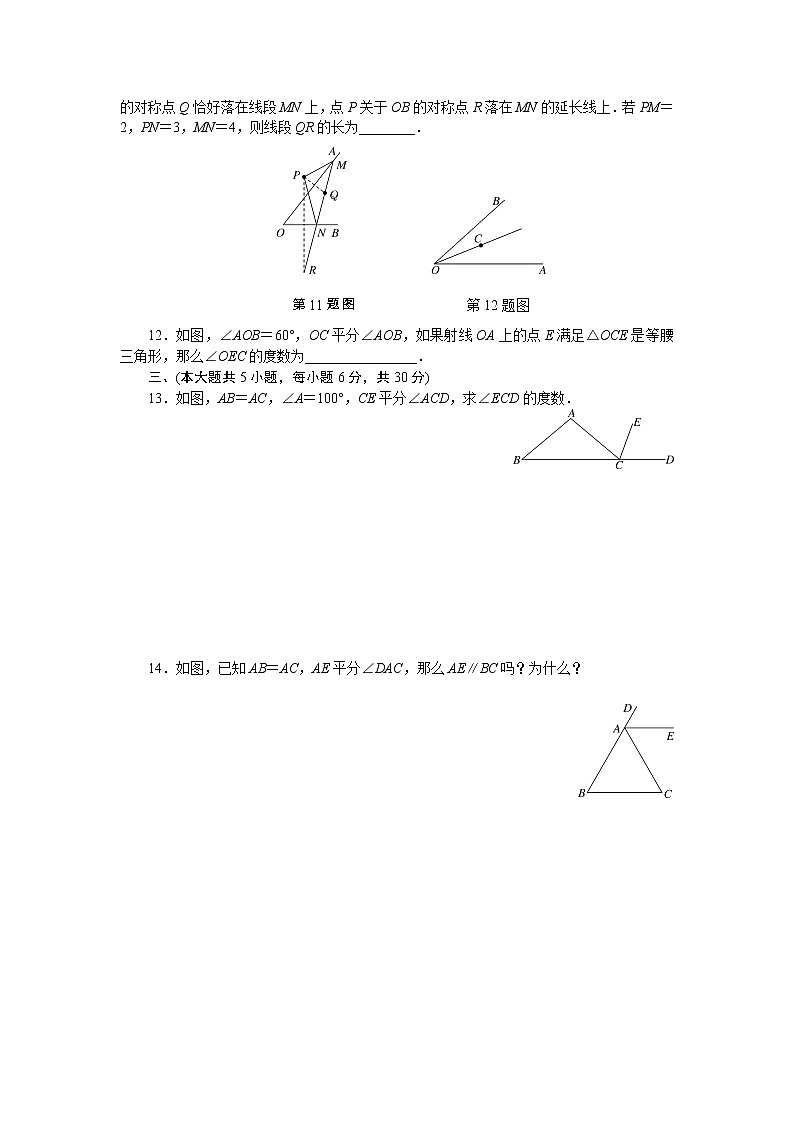
11．如图，点P是∠AOB外的一点，点M，N分别是∠AOB两边上的点，点P关于OA的对称点Q恰好落在线段MN上，点P关于OB的对称点R落在MN的延长线上．若PM＝2，PN＝3，MN＝4，则线段QR的长为________．

第11题图                第12题图

12．如图，∠AOB＝60°，OC平分∠AOB，如果射线OA上的点E满足△OCE是等腰三角形，那么∠OEC的度数为________________．

三、(本大题共5小题，每小题6分，共30分)

13．如图，AB＝AC，∠A＝100°，CE平分∠ACD，求∠ECD的度数．

14．如图，已知AB＝AC，AE平分∠DAC，那么AE∥BC吗？为什么？

15．如图，在△ABC中，∠C＝∠ABC，BE⊥AC，△BDE是正三角形．求∠C的度数．

16．如图，AB比AC长2cm，BC的垂直平分线交AB于点D，交BC于点E，△ACD的周长是14cm，求AB和AC的长．

17．如图是由一个正方形和一个等腰直角三角形组成的图形．试分别在图①和图②中，用无刻度的直尺通过连线的方式按要求作图：

(1)在图①中画出一个小正方形ABCD；

(2)在图②中画出图形的对称轴l.

四、(本大题共3小题，每小题8分，共24分)

18．如图，从①∠B＝∠C；②∠BAD＝∠CDA；③AB＝DC；④BE＝CE四个等式中选出两个作为条件，证明△AED是等腰三角形(写出一种即可)．

19．如图，在平面直角坐标系中，A(－3，2)，B(－4，－3)，C(－1，－1)．

(1)在图中作出ABC关于y轴对称的△A1B1C1；

(2)写出点A1，B1，C1的坐标：A1________，B1________，C1________；

(3)在y轴上画出点P，使PB＋PC最小．

20．如图，OE平分∠AOB，EF∥OB，EC⊥OB.

(1)求证：OF＝EF；

(2)若∠BOE＝15°，EC＝5，求OF的长．

五、(本大题共2小题，每小题9分，共18分)

21．如图，在△ABC中，AB＝AC，点D、E、F分别在边AB、BC、AC上，且BE＝CF，BD＝CE.

(1)求证：△DEF是等腰三角形；

(2)当∠A＝40°时，求∠DEF的度数．

22．如图，已知∠MAN＝120°，AC平分∠MAN，∠ABC＋∠ADC＝180°.求证：

(1)DC＝BC；

(2)AB＋AD＝AC.

六、(本大题共12分)

23．如图，在平面直角坐标系中，点A的坐标为(1，0)，以线段OA为边在第四象限内作等边三角形AOB，点C为x轴正半轴上一动点(OC＞1)，连接BC，以线段BC为边在第四象限内作等边△CBD，连接DA并延长，交y轴于点E.

(1)△OBC与△ABD全等吗？判断并证明你的结论；

(2)当点C运动到什么位置时，以A，E，C为顶点的三角形是等腰三角形？

参考答案与解析

1．D　2.C　3.D　4.A　5.D

6．C　解析：分别以A，B，C为等腰三角形的顶点的等腰三角形有4个，如图①，分别为△ABD，△ABE，△ABF，△ACG，∴满足条件的直线有4条；分别以AB，AC，BC为底的等腰三角形有3个，如图②，分别为△ABH，△ACM，△BCN，∴满足条件的直线有3条．综上所述，满足条件的直线共有7条，故选C.

7．5　8.3　9.1　10.7cm　11.5

12．120°或75°或30°　解析：∵∠AOB＝60°，OC平分∠AOB，∴∠AOC＝30°.当△OCE为等腰三角形时，有如下情况．如图．①当E在E1时，OE＝CE，∴∠OCE＝∠AOC＝30°，∴∠OEC＝180°－30°－30°＝120°；②当E在E2时，OC＝OE，则∠OCE＝∠OEC＝(180°－30°)＝75°；③当E在E3时，OC＝CE，则∠OEC＝∠AOC＝30°.综上所述，∠OEC的度数为120°或75°或30°.

13．解：∵AB＝AC，∠A＝100°，∴∠B＝(180°－100°)÷2＝40°，(2分)∴∠ACD＝100°＋40°＝140°.(4分)∵CE平分∠ACD，则∠ECD＝70°.(6分)

14．解：AE∥BC.(2分)理由如下：∵AB＝AC，∴∠B＝∠C.由三角形的外角性质得∠DAC＝∠B＋∠C＝2∠B.(4分)∵AE平分∠DAC，∴∠DAC＝2∠DAE，∴∠B＝∠DAE，∴AE∥BC.(6分)

15．解：∵△BDE是正三角形，∴∠DBE＝60°.(1分)∵BE垂直AC，∠BEA＝90°，∴∠A＝90°－60°＝30°.(3分)∵∠ABC＋∠C＋∠A＝180°，∠C＝∠ABC，∴∠C＝＝75°.(6分)

16．解：∵BC的垂直平分线交AB于点D，交BC于点E，∴BD＝DC.(2分)∵△ACD的周长是14cm，∴AD＋DC＋AC＝14cm，∴AD＋BD＋AC＝AB＋AC＝14cm.(4分)∵AB比AC长2cm，∴AB－AC＝2cm，∴AC＝6cm，AB＝8cm.(6分)

17．解：(1)如图①所示．(3分)

(2)如图②所示．(6分)

18．解：选择的条件是：①∠B＝∠C，②∠BAD＝∠CDA(或①③，①④，②③)．(2分)证明如下：在△BAD和△CDA中，

∵∴△BAD≌△CDA(AAS)，∴∠ADB＝∠DAC，(6分)∴AE＝DE，∴△AED为等腰三角形．(8分)

19．解：(1)如图所示，△A1B1C1即为所求．(2分)

(2)(3，2)　(4，－3)　(1，－1)(5分)

(3)如图所示，连接B1C，交y轴于点P，点P即为所求．(8分)

20．(1)证明：∵OE平分∠AOB，∴∠BOE＝∠AOE.∵EF∥OB，∴∠BOE＝∠OEF，(2分)∴∠OEF＝∠FOE，∴OF＝EF.(4分)

(2)解：如图，过E作ED⊥OA于D.∵CE⊥OB，OE平分∠AOB，∴DE＝CE＝5.(6分)∵∠BOE＝15°，∴∠OEF＝∠FOE＝15°，∴∠EFD＝30°，∴EF＝2DE＝10，∴OF＝EF＝10.(8分)

21．(1)证明：∵AB＝AC，∴∠B＝∠C.在△DBE和△ECF中，∴△DBE≌△ECF(SAS)，(3分)∴DE＝EF，∴△DEF是等腰三角形．(4分)

(2)解：由(1)可知△DBE≌△ECF，∴∠1＝∠3.(5分)∵∠A＋∠B＋∠C＝180°，∠A＝40°，∠B＝∠C，∴∠B＝(180°－40°)＝70°，∴∠1＋∠2＝110°，(7分)∴∠3＋∠2＝110°，∴∠DEF＝180°－110°＝70°.(9分)

22．证明：(1)如图，在AN上截取AE＝AC，连接CE.(2分)∵AC平分∠MAN，∠MAN＝120°，∴∠CAB＝∠CAD＝60°，∴△ACE是等边三角形，∴∠AEC＝60°，AC＝EC＝AE.又∵∠ABC＋∠ADC＝180°，∠ABC＋∠EBC＝180°，∴∠ADC＝∠EBC.(4分)在△ADC和△EBC中，∴△ADC≌△EBC(AAS)，∴DC＝BC.(6分)

(2)由(1)知△ADC≌△EBC，AE＝AC，∴AD＝BE，∴AB＋AD＝AB＋BE＝AE，∴AB＋AD＝AC.(9分)

23．解：(1)△OBC≌△ABD.(1分)证明如下：∵△AOB，△CBD都是等边三角形，∴OB＝AB，CB＝DB，∠ABO＝∠DBC＝60°，∴∠OBC＝∠ABD.(3分)在△OBC和△ABD中，∴△OBC≌△ABD(SAS)．(5分)

(2)由(1)知△OBC≌△ABD，∴∠BAD＝∠BOC＝60°.又∵∠OAB＝60°，∴∠OAE＝180°－60°－60°＝60°，∴∠EAC＝120°，∠OEA＝30°，∴以A，E，C为顶点的三角形是等腰三角形时，AE和AC是腰．(8分)∵在Rt△AOE中，OA＝1，∠OEA＝30°，∴AE＝2，(9分)∴AC＝AE＝2，∴OC＝1＋2＝3，∴点C的坐标为(3，0)．(11分)∴当点C的坐标为(3，0)时，以A，E，C为顶点的三角形是等腰三角形．(12分)