2015-2016学年杭州市四季青中学八上期中数学试卷

这是一份2015-2016学年杭州市四季青中学八上期中数学试卷，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. 下列语句是命题的是
A. 画两条相等的线段B. 在线段 AB 上取点 P
C. 等腰三角形是轴对称图形D. 垂线段最短吗?

2. 下列图形中，对称轴最多的是
A. 等腰三角形B. 等边三角形
C. 直角三角形D. 等腰直角三角形

3. 已知 AD 是 △ABC 的中线，BE 是 △ABD 的中线，若 △ABC 的面积为 20，则 △ABE 的面积为
A. 5B. 10C. 15D. 18

4. 如图是玩具拼图模板的一部分，已知 △ABC 的六个元素，则下面甲、乙、丙三个三角形中能和 △ABC 完全重合的是
A. 甲和丙B. 丙和乙C. 只有甲D. 只有丙

5. 如果 a>b，下列各式中不正确的是
A. a−4>b−4B. −a3<−b3
C. −2a<−2bD. −5+a<−5+b

6. 不等式组 2x−1>0,x+1≥0 的解集是
A. x>12B. −1≤x<12C. x<12D. x≥−1

7. 下列选项中，可以用来证明命题“若 a2>1，则 a>1 ”是假命题的反例是
A. a=−2B. a=−1C. a=1D. a=2

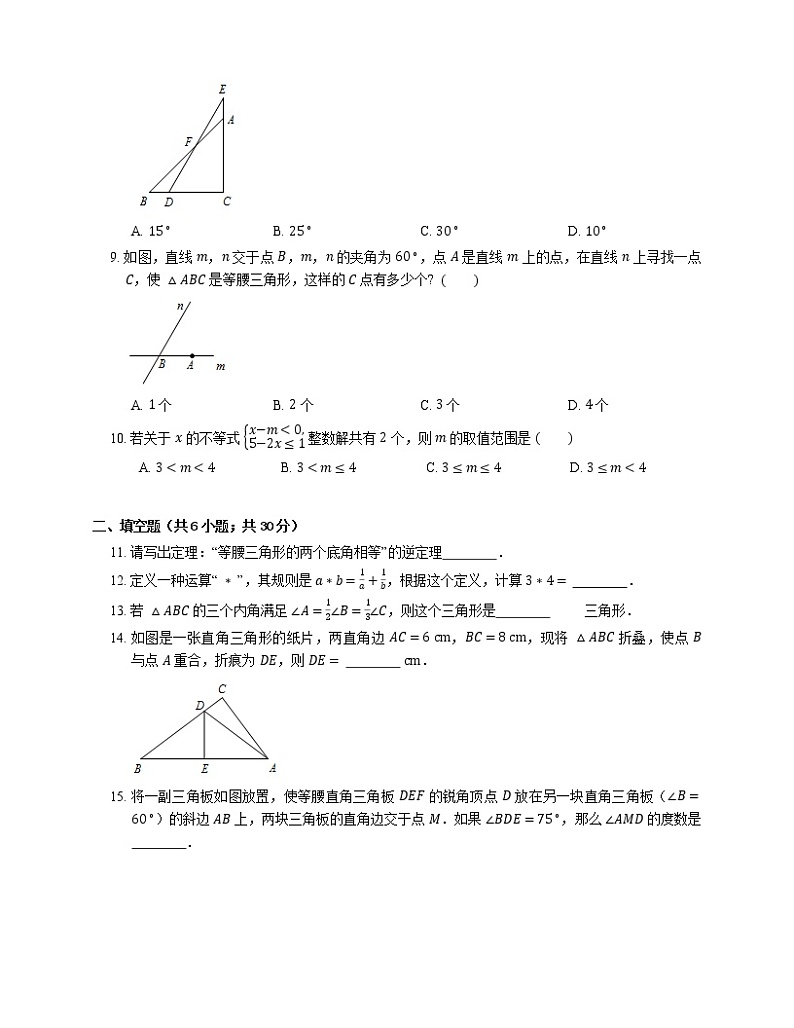
8. 如图，一副分别含有 30∘ 和 45∘ 角的两个直角三角板，拼成如下图形，其中 ∠C=90∘，∠B=45∘，∠E=30∘，则 ∠BFD 的度数是
A. 15∘B. 25∘C. 30∘D. 10∘

9. 如图，直线 m，n 交于点 B，m，n 的夹角为 60∘，点 A 是直线 m 上的点，在直线 n 上寻找一点 C，使 △ABC 是等腰三角形，这样的 C 点有多少个?
A. 1 个B. 2 个C. 3 个D. 4 个

10. 若关于 x 的不等式 x−m<0,5−2x≤1 整数解共有 2 个，则 m 的取值范围是
A. 3
二、填空题（共6小题；共30分）
11. 请写出定理：“等腰三角形的两个底角相等”的逆定理 ．

12. 定义一种运算“ * ”，其规则是 a*b=1a+1b，根据这个定义，计算 3*4= ．

13. 若 △ABC 的三个内角满足 ∠A=12∠B=13∠C，则这个三角形是 三角形．

14. 如图是一张直角三角形的纸片，两直角边 AC=6 cm，BC=8 cm，现将 △ABC 折叠，使点 B 与点 A 重合，折痕为 DE，则 DE= cm．

15. 将一副三角板如图放置，使等腰直角三角板 DEF 的锐角顶点 D 放在另一块直角三角板（∠B=60∘）的斜边 AB 上，两块三角板的直角边交于点 M．如果 ∠BDE=75∘，那么 ∠AMD 的度数是 ．

16. 三角形中一个内角 α 是另一个内角 β 的两倍时，我们称此三角形为“特征三角形”，其中 α 称为“特征角”，如果一个“特征三角形”的“特征角”为 110∘，那么这个“特征三角形”的最小内角的度数为 ．

三、解答题（共7小题；共91分）
17. 如图，将三角尺的直角顶点放在直线 a 上，a∥b，∠1=50∘，∠2=60∘，求 ∠3 的度数．

18. （1）解不等式 7x−2≤9x+2，并把解表示在数轴上；
（2）解不等式组：x−25<0,22x−5≤34x+2, 并写出该不等式组的整数解．

19. 如图，已知 △ABC，其中 AB=AC．
（1）作 AC 的垂直平分线 DE，交 AC 于点 D，交 AB 于点 E，连接 CE（尺规作图，不写作法，保留作图痕迹）；
（2）在（1）所作的图中，若 BC=7，AC=9，求 △BCE 的周长．

20. 某业主贷款 2.2 万元购进一台机器，生产某种产品．已知产品的成本是每个 5 元，售价是每个 8 元，应付的税款和其他费用是售价的 10%．若每个月能生产、销售 2000 个产品，问至少几个月后能赚回这台机器的贷款?

21. 如图，已知 △ABC 是等边三角形，D 为边 AC 的中点，AE⊥EC，BD=EC．
（1）求证：△BDA≌△CEA；
（2）请判断 △ADE 是什么三角形，并说明理由．

22. 如图，在等腰 Rt△ABC 中，AB=AC，CE 是 ∠ACB 的平分线，ED⊥BC，垂足为 D．
（1）请写出图中所有的等腰三角形（不包括 △ABC）
（2）请判断 AD 与 CE 是否垂直，并说明理由．
（3）如果 AB=2，求 AC+AE 的值．

23. 数学课上，李老师出示了如下框中的题目．
小敏与同桌小聪讨论后，进行了如下解答：
（1）特殊情况•探索结论
当点 E 为 AB 的中点时，如图 1，确定线段 AE 与的 DB 大小关系．请你直接写出结论：AE DB（填“ > ”，“ < ”或“ = ”）．
（2）特例启发，解答题目
解：题目中，AE 与 DB 的大小关系是：AE DB（填“ > ”，“ < ”或“ = ”）．
理由如下：如图 2，过点 E 作 EF∥BC，交 AC 于点 F，（请你完成以下解答过程）
（3）拓展结论，设计新题
在等边三角形 ABC 中，点 E 在直线 AB 上，点 D 在直线 BC 上，且 ED=EC．若 △ABC 的边长为 1，AE=2，求 CD 的长．
答案
第一部分
1. C
2. B
3. A
4. A
5. D
6. A
7. A【解析】所谓反例，是使原命题的条件成立，而结论不成立，四个选项中，选项 B，C 不符合原命题的条件故应先排除，而选项 D 跟原命题的结论相符，所以答案应为 A．
8. A
9. B【解析】
10. B
【解析】x−m<0 ⋯⋯①,5−2x≤1 ⋯⋯②.
解①得 x解②得 x≥2．
则不等式组的解集是 2≤x ∵ 不等式组有 2 个整数解，
∴ 整数解是 2，3．
则 3第二部分
11. 有两个角相等的三角形是等腰三角形
12. 712
13. 直角
14. 154
15. 90∘
【解析】∵∠B=60∘，
∴∠A=30∘．
∵∠BDE=75∘，∠FDE=45∘，
∴∠ADF=180∘−75∘−45∘=60∘．
∴∠AMD=180∘−30∘−60∘=90∘．
16. 15∘
第三部分
17. 如图
∠1=50∘，∠2=60∘，
∴∠4=180∘−∠1−∠2=180∘−50∘−60∘=70∘，
∴∠5=∠4=70∘．
∵a∥b，
∴∠3=∠5=70∘．
18. （1） 移项，得
−2x≤4,
系数化 1，得
x≥−2.
数轴：
（2） x−25<0, ⋯⋯①22x−5≤34x+2, ⋯⋯②
由 ① 得 x<2；
由 ② 得 x≥−2．
∴ 不等式组的解集为 −2≤x<2，则不等式组的整数解为 −2，−1，0，1．
19. （1） 如图所示：
直线 DE 即为所求．
（2） ∵AB=AC=9，
∵DE 垂直平分 AB，
∴AE=EC．
∴△BCE 的周长=BC+BE+CE=BC+BE+AE=BC+AB=16．
20. 设至少需要 x 个月才能赚回这台机器款．
由题意得
2000×8−2000×5−2000×8×10%×x≥22000,
解得
x≥5,
答：至少需要 5 个月才能赚回这台机器．
21. （1） ∵AE⊥EC，
∴∠AEC=90∘．
在 等边三角形 △ABC 中，
∵D 是 AC 中点，
∴∠BDA=90∘．
在 △RtBDA 和 △RtCEA 中，
BD=EC,AB=AC,
∴△BDA≌△CEA HL．
（2） ∵△BDA≌△CEA，
∴AE=AD．
∵Rt△AEC 中，D 是 AC 中点，
∴DE=12AC=AD．
∴AD=DE=AE．
∴△ADE 是等边三角形．
22. （1） △BDE，△ADE，△ACD
【解析】根据等腰三角形的定义判断，△ABC 等腰直角三角形，CE 为角平分线；可证 △ACE≌△DCE，即 AC=CD，AE=DE，所以 △ACD 和 △ADE 均为等腰三角形；∠B=45∘，ED⊥BD，△EDB 也符合题意．
（2） AD⊥CE．
证明：由 CE 为 ∠ACB 的平分线，
知 ∠ACE=∠DCE，∠CAE=∠CDE=90∘，CE=CE，
∴△ACE≌△DCE．
∴AC=CD．
∴△ACD 是等腰三角形．
∴AD⊥CE．
（3） 有（2）得 △ACE≌△DCE，
∴AC=CD，AE=DE．
又 △ABC 是等腰直角三角形，∠BAC=90∘，AB=2，
∴∠B=45∘，BC=22．
∵ED⊥BC，
∴△BDE 为等腰直角三角形，
∴DE=BD，
即 AC+AE=BD+DC=BC=22．
23. （1） =
【解析】∵ED=EC，E 为 AB 中点，
∴∠BDE=∠BCE=30∘，AE=BE．
∵∠ABC=60∘，
∴∠BED=30∘．
∴DB=BE=AE．
（2） =
在等边 △ABC 中，∠ABC=∠ACB=∠BAC=60∘，AB=BC=AC，
∵EF∥BC，
∴∠AEF=∠ABC，∠AFE=∠ACB，
∴∠AEF=∠AFE=∠BAC=60∘，
∴AE=AF=EF，
∴AB−AE=AC−AF，即 BE=CF，
∵∠ABC=∠EDB+∠BED，∠ACB=∠ECB+∠FCE，
∵ED=EC，
∴∠EDB=∠ECB，
∴∠BED=∠FCE，
在 △DBE 和 △EFC 中，
ED=EC,∠DEB=∠ECF,EB=FC.
∴△DBE≌△EFC SAS，
∴DB=EF，
∴AE=BD．
（3） 分为四种情况：
如图
∵AB=AC=1，AE=2，
∴B 是 AE 的中点．
∵△ABC 是等边三角形，
∴AB=AC=BC=1，△ACE 是直角三角形（根据直角三角形斜边的中线等于斜边的一半）．
∴∠ACE=90∘，∠AEC=30∘．
∴∠D=∠ECB=∠BEC=30∘，∠DBE=∠ABC=60∘．
∴∠DEB=180∘−30∘−60∘=90∘，即 △DEB 是直角三角形．
∴BD=2BE=2（30∘ 所对的直角边等于斜边的一半），即 CD=1+2=3．
如图，过 A 作 AN⊥BC 于 N，过 E 作 EM⊥CD 于 M．
∵ 等边三角形 ABC，EC=ED，
∴BN=CN=12BC=12，CM=MD=12CD，
∵AN∥EM，
∴ABAE=BNMN，
∵△ABC 边长是 1，AE=2，
∴12=12MN，
∴MN=1，
∴CM=MN−CN=1−12=12，
∴CD=2CM=1；
如图
∵∠ECD>∠EBC（∠EBC=120∘），而 ∠ECD 不能大于 120∘，否则 △EDC 不符合三角形内角和定理，
∴ 此时不存在 EC=ED；
如图
∵∠EDC<∠ABC，∠ECB>∠ACB，
∵∠ABC=∠ACB=60∘，
∴∠ECD>∠EDC，即此时 ED≠EC．
∴ 此时情况不存在．
答：CD 的长是 3 或 1．