手拉手模型                    

模型  手拉手

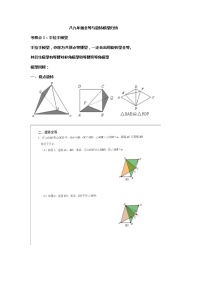
    如图，△ABC是等腰三角形、△ADE是等腰三角形，AB=AC，AD=AE，

∠BAC=∠DAE=。

    结论：△BAD≌△CAE。

等腰三角形分为:等边三角形、等腰直角、任意等腰三角形，几种特殊情况分别讨论如下：

1、等边三角形

条件：△OAB，△OCD均为等边三角形

结论：；；

导角核心：

2、等腰直角三角形

条件：△OAB，△OCD均为等腰直角三角形

结论：；；

导角核心：

3、任意等腰三角形

条件：△OAB，△OCD均为等腰三角形，且∠AOB = ∠COD

结论：；；

核心图形：

核心条件：；；

接下来，将针对以“两个等边三角形”为载体的模型与方法进行分析和讲解。

两个等边三角形放在一起，最常见的就是“手拉手模型”，这个模型包含了许多非常重要的结论和方法！

重点给大家分享一下两个等边三角形放在一起的模型，其中最最重要的就是 两个等边三角形共顶点的模型，俗称 “手拉手模型”。

针对这个模型的研究，一般分为三个方向：

一、不变性

二、特殊位置出现的特殊结论(临界点)

三、增加部分条件得出的新结论

首先，我们来研究一下这个模型中都包含哪些 “不变性质”。

第一个不变性质就是全等，如下图：

无论两个等边三角形的相对位置如何△ACD≌△BCE（SAS）始终成立。

第二个不变性质是角度问题，如下图：

根据第一条性质的全等，得出∠1=∠2，再依据“蝴蝶模型”或者“8”字模型倒角或者“四点共圆”都可以得出AD和BE的夹角 ∠APB=60°，这个结论不随等边三角形的相对位置变化而变化，也具有不变性。

第三个不变性质是角平分线，如下图：

CP始终平分∠BPD，也就是说∠BPC=∠DPC =60°始终成立。

证法1：

如下图，分别作BE和AD的垂线段CH和CK，由△ACD≌△BCE（SAS），可以知道△ACD和△BCE的面积相等，底也相等，全等三角形对应高也相等，所以高CH=CK.根据角平分线的性质，可以知道CP平分∠BPD.

证法2：

如下图，根据 ∠1=∠2，AC=BC，在BP上截取BF=AP，则△ACP≌△BCF（SAS），

于是，CF=CP，∠FCP=∠BCA=60°，所以△FPC是等边三角形。

这样，也就得出∠FPC=∠DPC=60°，CP平分∠BPD.

第四个不变性质就是“等边+120°模型”（这里中考不做要求）

这个模型在这里始终会出现。

对角互补旋转

也就是说在这个模型中，BP=CP+AP，PE=CP+PD始终成立。

最后，以上这些结论看似简单，但是要想让学生彻底掌握，需要进行巩固和强化训练，训练的方式最好就变换不同的角度和相对位置，让自己再去证明一次，找到所有的全等、不变角、角平分线、线段和差模型、等性质。

比如，进行以下四个图形位置的训练：

二、特殊位置出现的特殊结论

手拉手模型共线

下面我先给大家继续介绍经典几何模型---手拉手模型，特殊位置下的特殊结论，这也是历年数学中考常考的几何压轴题型之一。

例1、在直线ABC的同一侧作两个等边三角形△ABD和△BCE，连接AE与CD，证明：

（1）△ABE≌△DBC

（2）AE=DC

（3）AE与DC的夹角为60

（4）△AGB≌△DFB

（5）△EGB≌△CFB

（6）BH平分∠AHC

（7）GF∥AC

解析：（1）∵△ABD和△BCE是等边三角形，

∴AB=DB，BC=BE，∠ABD=∠CBE=60°，

∴∠ABD+∠DBE=∠CBE+∠DBE，

即∠DBC=∠ABE，

在△ABE和△DBC中，

易证明△ABE≌△DBC（SAS）

(2) ∵△ABE≌△DBC（SAS）

∴AE=CD；

(3) ∵△ABE≌△DBC，

∴∠AEB=∠DCB.

又∵∠HFE=∠BFC(对顶角相等)

△HFE和△BFC中，

∠EHF=180-∠AEB-∠HFE;

∠CBF=180-∠DCB -∠BFC，

∴∠EHF=∠CBF=60

∴AE与DC的夹角为60。

(4)AB=BD,BG=BF,

∠ABG=∠DBF=60

∴△AGB≌△DFB

(5)EB=EC,BG=BF, ∠EBG=∠CBF=60

∴△EGB≌△CFB

(6)过B作BM垂直AE于M，BN垂直CD于N。

证明△ABM ≌△DBM，则BM=BN

∴BH平分∠AHC

（7）∵△AGB≌△DFB

∴BG=BF

又∠GBF=60，

∴GBF为等边三角形

∴∠GFB=EBC=60,

∴GF∥AC

三、增加部分条件得出的新结论

（8）线段和差关系

        AH=DH+BH 或  CH=BH+HE

    (提示：在AH取I,HI=BH CH取P,HP=BH)

（9）△BGF等边三角形

（10）四点共圆:

           ABHD四点共圆，

           BFHG四点共圆，

           CBHE四点共圆

总结： “两个共顶点的等边三角形的手拉手模型”，对于这个模型的研究，给出了三个方向：

一、不变性(三个)

二、特殊位置出现的特殊结论

三、增加部分条件得出的新结论

我们本次内容仅仅涉及了到对于基本模型的不变性质的研究。这些不变性质涉及到了全等、角度、角平分线以及等边+120度线段和差模型等。