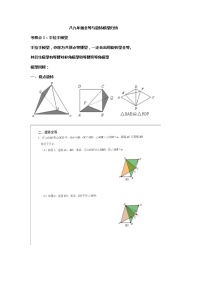
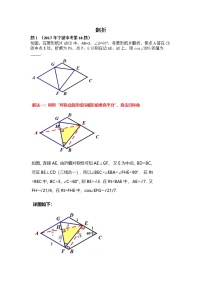
【专项练习】备战中考数学58种模型专练 46.尺规作图（含答案）

无刻度直尺作图专练

一、线段n等分点的找法：“X”型相似的构造

1. 做出BC中点P：

①根据长方形性质找中点                                 ②根据平行四边形性质找中点

2. 三等分点

①在BC上找点P，使PB:PC=2:1                           ②在BC上找点P，使PC:PB=2:1

总结：构造线段n等分点：

①在一组平行线里找到线段两端；

②在平行线上找到1与（n-1）长度的线段；

③连接端点与已知线段交点即为所求。

练一练：

1.仅用无刻度直尺作出下列三角形的重心G：

二、垂线段的构造：

1.在平面内找到点D，使BD=BC且BD⊥BC          2.过AD⊥BC交BC于D                               

练一练：三角形高（垂线）的构造，作出下列三角形的垂心H：

总结：做已知线段的垂线方法：

①利用已知线段构造“K”型全等（三垂直全等）；

②利用已知点与所做直角边，构造平行四边形；

③平行四边形与已知线段交点即为所求。

三、线段垂直平分线的构造：

作出BC的垂直平分线： ①找中点；

②构造三垂直全等；

③过中点构造构造平行四边形；

练一练:

四、角平分线的构造:

1.做出∠ABC的角平分线BD

①等腰三角形三线合一                                        ②平行+等腰→角平分线

练一练：做出∠ABC的角平分线

特征：边（线段）为整数，易在已知线段（平行线）上截取

思考：仅用无刻度直尺作出下列三角形的内心I ：

五、旋转类：

1.如图，在下列6×6和10×10的网格中，横、纵坐标均为整点的数叫做格点.

（1）如图1，画∠MHN的角平分线HP，寻找一个格点P并写出其坐标；

（2）如图2，A（1，－3）、B（4,0）、C（0,4）都是格点，要求在下图中仅用无刻度的直尺作图：将△ABC绕点A顺时针旋转角度α得到△AB1C1，α＝∠BAC，其中B、C的对应点分别为B1、C1，操作如下：

第一步：找一个格点D，连接AD，使∠DAB＝∠CAB，

第二步：找两个格点C1、E，连接C1E交AD于B1；

第三步：连接AC1，则△AB1C1交即为所做出的图形.

请你按步骤完成作图，并直接写出D、C1、E三点的坐标.

2.如图，已知A(-1，1)，B(-6，2)，C(-3，4) ．

(1) 先作△ABC关于y轴的对称图形得△A1B1C1，请画出△A1B1C1；

(2) 再将△A1B1C1向下平移5个单位得△A2B2C2，请画出并写出A2点坐标；

(3)请先在网格线中找一个格点D，使∠DAB=∠CAB，再将△ABC绕A点逆时针旋转∠BAC得△AB3C3，请只用圆规和直尺画出图形△AB3C3．

总结：①在已知边上找到某点对应点；

②旋转已知角度，利用好45度，将角分割成45度；

③构造全等三角形。

作业

1.已知，在平面直角坐标系中，A(4，0)，B(4，4)，C(0，4)，E(3，0).

连接BE，点G在y轴上，按下列步骤作∠AEB＝∠BEG.

方法一：①找格点F，连接BF，使∠FBE＝45°；

②BF交OC于G点，则∠AEB＝∠BEG，简述理由.

对照本节课，有方法二，简述理由：

20． (本小题满分8分) 如图，在每个小正方形的边长为1的网格中，△ABC的顶点A， B，C均在格点上．

(1)∠ACB的大小为____________°；
(2)在如图所示的网格中以A为中心，取旋转角等于∠BAC，把△ABC逆时针旋转，请用无刻度的直尺，画出旋转后的△AB' C'，保留作图痕迹，不要求证明；
(3)点P是BC边上任意一点，在上题的旋转过程中，点P的对应点为P'，当线段CP'最短时，CP'的长度为__________．
 

变式：(1)在如图所示的网格中以B为中心，取旋转角等于∠ABC，把△ABC逆时针旋转，请用无刻度的直尺，画出旋转后的△AB' C'，保留作图痕迹，不要求证明；
      (2)点P是BC边上任意一点，在上题的旋转过程中，点P的对应点为P'，当线段CP'最短时，CP'的长度为__________．