(山东版)2021年中考数学模拟练习卷09（含答案）

这是一份(山东版)2021年中考数学模拟练习卷09（含答案），共19页。试卷主要包含了解答题等内容，欢迎下载使用。

中考数学模拟练习卷
一、选择题（本题共14小题，每小题3分，共42分）在每小题所给的四个选项中，只有一项是符合题目要求的。
1．（3分）计算：﹣3﹣5的结果是（　　）
A．﹣2 B．2 C．﹣8 D．8
【解答】解：﹣3﹣5=﹣8．
故选：C．
　
2．（3分）计算：（﹣x）3•2x的结果是（　　）
A．﹣2x4 B．﹣2x3 C．2x4 D．2x3
【解答】解：（﹣x）3•2x=﹣x3•2x
=﹣2x4．
故选：A．
　
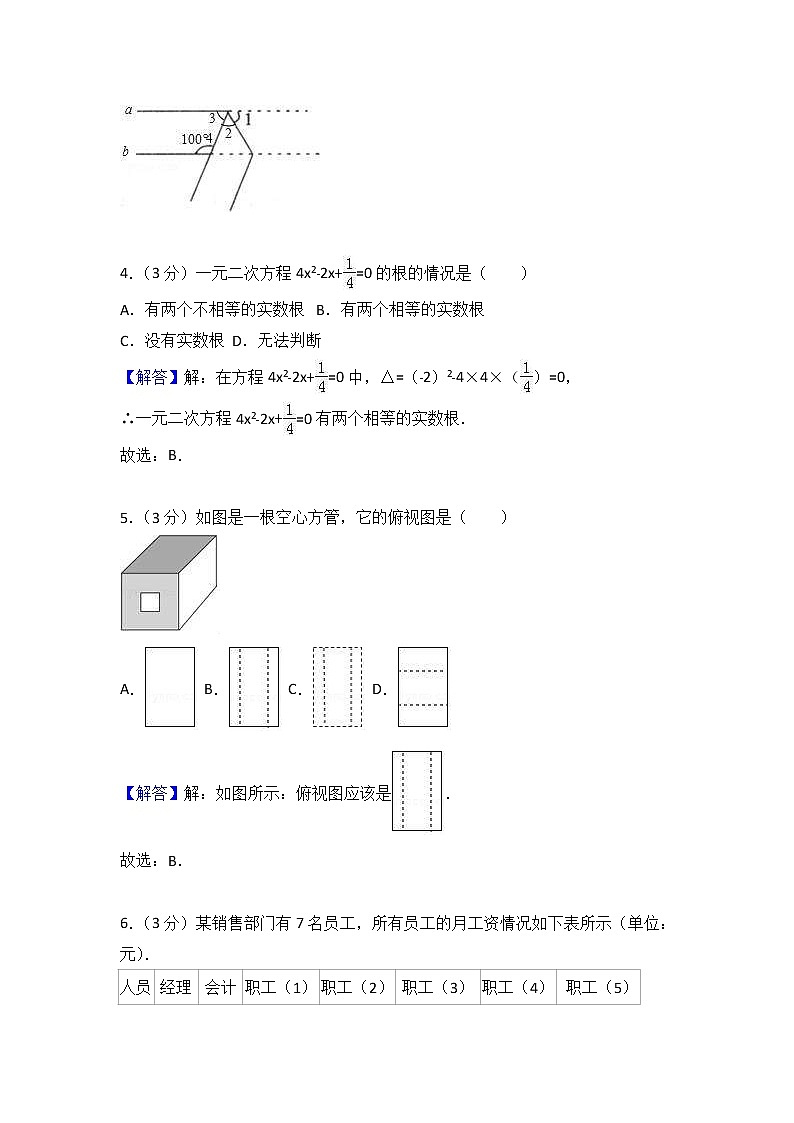
3．（3分）一个两边平行的纸条，如图那样折叠一下，则∠1的度数是（　　）

A．30° B．40° C．50° D．60°
【解答】解：根据题意得：a∥b，∠1=∠2，∠4=100°，
∴∠3+∠4=180°，
∴∠3=80°，
∵∠1+∠2+∠3=180°，
∴∠1==50°．
故选：C．

　
4．（3分）一元二次方程4x2﹣2x+=0的根的情况是（　　）
A．有两个不相等的实数根 B．有两个相等的实数根
C．没有实数根 D．无法判断
【解答】解：在方程4x2﹣2x+=0中，△=（﹣2）2﹣4×4×（）=0，
∴一元二次方程4x2﹣2x+=0有两个相等的实数根．
故选：B．
　
5．（3分）如图是一根空心方管，它的俯视图是（　　）

A． B． C． D．
【解答】解：如图所示：俯视图应该是．
故选：B．
　
6．（3分）某销售部门有7名员工，所有员工的月工资情况如下表所示（单位：元）．
人员
经理
会计
职工（1）
职工（2）
职工（3）
职工（4）
职工（5）
工资
5000
2000
1000
800
800
800
780
则比较合理反映该部门员工工资的一般水平的数据是（　　）
A．平均数 B．平均数和众数
C．中位数和众数 D．平均数和中位数
【解答】解：平均数：（5000+2000+1000+800+800+800+780）÷7≈1597（元），
中位数：800（元），
众数：800（元），员工的月工资能到平均工资的只有两人，不能反映一般水平，而员工的月工资能到800（元）的有6人，
所以能比较合理反映该部门员工工资的一般水平的数据是中位数和众数．
故选：C．
　
7．（3分）不等式组的整数解是（　　）
A．1，2 B．0，1，2 C．﹣1，1，2 D．﹣1，0，1，2
【解答】解：，
解①得，x＞﹣，
解②得，x≤2，
不等式组的解集为﹣＜x≤2，
∴不等式组的整数解为﹣1，0，1，2．[来源:学&科&网]
故选：D．
　
8．（3分）如图，在⊙O中，OC∥AB，∠A=20°，则∠1等于（　　）[来源:Zxxk.Com]

A．40° B．45° C．50° D．60°
【解答】解：∵OC∥AB，
∴∠C=∠A=20°，
又∵∠O=2∠A=40°，
∴∠1=∠O+∠C=20°+40°=60°．
故选：D．
　
9．（3分）在反比例函数y=图象上有两点A（x1，y1），B（x2，y2），x1＜0＜x2，y1＜y2，则m的取值范围是（　　）
A．m＞ B．m＜ C．m≥ D．m≤
【解答】解：∵x1＜0＜x2时，y1＜y2，
∴反比例函数图象在第一，三象限，
∴1﹣3m＞0，
解得：m＜．
故选：B．
　
10．（3分）如图，边长为a，b的长方形的周长为13，面积为10，则a3b+ab3的值为（　　）

A．37.5 B．65 C．130 D．222.5
【解答】解：∵a+b=，ab=10，
∴a3b+ab3=ab[（a+b）2﹣2ab]=10×（﹣20）=222.5，
故选：D．
　
11．（3分）如图，OA=OB，∠A=∠B，有下列3个结论：①△AOD≌△BOC，②△ACE≌△BDE，③点E在∠O的平分线上，其中正确的结论个数是（　　）

A．0 B．1 C．2 D．3
【解答】解：∵OA=OB，∠A=∠B，∠O=∠O，
∴△AOD≌△BOC（ASA），故①正确；
∴OD=CO，
∴BD=AC，
∴△ACE≌△BDE（AAS），故②正确；
∴AE=BE，
连接OE，∴△AOE≌△BOE（SSS），
∴∠AOE=∠BOE，
∴点E在∠O的平分线上，故③正确，
故选：D．
　
12．（3分）四个形状、大小相同的长方形，如图，拼成一个大的长方形，如果大长方形的周长为280厘米，那么，每块小长方形的面积是（　　）

A．900平方厘米 B．1200平方厘米 C．1600平方厘米 D．1800平方厘米
【解答】解：设每块小长方形的长为xcm，宽为ycm，
则可列方程组，
解得．
则每块小长方形的面积=60×20cm=1200（平方厘米）．
答：每块小长方形的面积是1200平方厘米．
故选：B．
　
13．（3分）如图所示，两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动，下列说法错误的是（　　）

A．四边形ACDF是平行四边形
B．当点E为BC中点时，四边形ACDF是矩形
C．当点B与点E重合时，四边形ACDF是菱形
D．四边形ACDF不可能是正方形
【解答】解：A、正确．∵∠ACB=∠EFD=30°，
∴AC∥DF，
∵AC=DF，
∴四边形AFDC是平行四边形．故正确．
B、错误．当E是BC中点时，无法证明∠ACD=90°，故错误．
C、正确．B、E重合时，易证FA=FD，∵四边形AFDC是平行四边形，
∴四边形AFDC是菱形，
D、正确．当四边相等时，∠AFD=60°，∠FAC=120°，∴四边形AFDC不可能是正方形．
故选：B．

　
14．（3分）已知抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=2，与x轴的一个交点坐标为（4，0），其部分图象如图所示，下列结论：
①抛物线过原点；
②4a+b+c=0；
③a﹣b+c＜0；
④抛物线的顶点坐标为（2，b）；
⑤当x＜2时，y随x增大而增大．
其中结论正确的是（　　）

A．①②③ B．③④⑤ C．①②④ D．①④⑤
【解答】解：①∵抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=2，与x轴的一个交点坐标为（4，0），
∴抛物线与x轴的另一交点坐标为（0，0），结论①正确；
②∵抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=2，且抛物线过原点，
∴﹣=2，c=0，
∴b=﹣4a，c=0，
∴4a+b+c=0，结论②正确；
③∵当x=﹣1和x=5时，y值相同，且均为正，
∴a﹣b+c＞0，结论③错误；
④当x=2时，y=ax2+bx+c=4a+2b+c=（4a+b+c）+b=b，
∴抛物线的顶点坐标为（2，b），结论④正确；
⑤观察函数图象可知：当x＜2时，y随x增大而减小，结论⑤错误．
综上所述，正确的结论有：①②④．
故选：C．
　
二、填空题（本大题共5小题，每小题3分，共15分)把答案填在题中横线上。
15．（3分）计算：|1﹣|﹣=　﹣1﹣　．
【解答】解：|1﹣|﹣
=﹣1﹣2
=﹣1﹣．
故答案为：﹣1﹣．
　
16．（3分）如图，△ABC中，点D在边AC上，∠ABD=∠C，AD=9，DC=7，那么AB=　12　．

【解答】解：∵∠ABD=∠C、∠BAD=∠CAB，
∴△ABD∽△ACB，
∴，即AB2=AC•AD，
∵AD=9，DC=7
∴AC=16，
∴AB=12，
故答案为：12
　
17．（3分）直线y=kx+b是由直线y=﹣2x平移得到的，且经过点P（2，0），则k+b的值为　2　．
【解答】解：∵直线y=kx+b是由直线y=﹣2x平移得到的，
∴y=kx+b中k=﹣2，
∵直线y=kx+b经过点P（2，0），
∴当x=2时，y=0，将其代入y=﹣2x+b，
解得：b=4．
则k+b=﹣2+4=2．
故答案为：2．
　
18．（3分）如图，将边长为6cm的正方形纸片ABCD折叠，使点D落在AB边中点E处，点C落在点Q处，折痕为FH，则线段AF的长是　　cm．

【解答】解：如图：

∵四边形ABCD是正方形，
∴AB=BC=CD=AD=6，
∵AE=EB=3，EF=FD，设EF=DF=x．则AF=6﹣x，
在RT△AEF中，∵AE2+AF2=EF2，
∴32+（6﹣x）2=x2，
∴x=，
∴AF=6﹣=cm，
故答案为．
　
19．（3分）甲、乙、丙、丁四位同学围成一圈依次循环报数，规定：①甲、乙、丙、丁首次报出的数依次为1、2、3、4，接着甲报5，乙报6…，后一位同学报出的数比前一位同学报出的数大1，按此规律，当报到的数是50时，报数结束；②若报出的数为3的倍数，则该报数的同学需拍手一次，在此过程中，甲同学需要拍手的次数为　4　．
【解答】解：∵甲、乙、丙、丁首次报出的数依次为1、2、3、4，接着甲报5，乙报6…按此规律，后一位同学报出的数比前一位同学报出的数大1．当报到的数是50时，报数结束；
∴50÷4=12余2，
∴甲共报数13次，分别为1，5，9，13，17，21，25，29，33，37，41，45，49，
∴报出的数为3的倍数，则报该数的同学需拍手一次．在此过程中，
甲同学需报到：9，21，33，45这4个数时，应拍手4次．
故答案为：4．
　
三、解答题(本大题共7小题，共63分)
20．（7分）化简：÷（1﹣）
【解答】解：原式=
=
=．
　
21．（7分）为了贯彻“减负增效”精神，掌握九年级600名学生每天的自主学习情况，某校学生会随机抽查了九年级的部分学生，并调查他们每天自主学习的时间．根据调查结果，制作了两幅不完整的统计图（图1，图2），请根据统计图中的信息回答下列问题：
（1）本次调查的学生人数是　40　人；
（2）图2中α是　54　度，并将图1条形统计图补充完整；
（3）请估算该校九年级学生自主学习时间不少于1.5小时有　330　人；
（4）老师想从学习效果较好的4位同学（分别记为A、B、C、D，其中A为小亮）随机选择两位进行学习经验交流，用列表法或树状图的方法求出选中小亮A的概率．

【解答】解：（1）∵自主学习的时间是1小时的有12人，占30%，
∴12÷30%=40，
故答案为：40； …（2分）

（2）×360°=54°，
故答案为：54；
40×35%=14；
补充图形如图：
故答案为：54；

（3）600×=330； …（2分）
故答案为：330；

（4）画树状图得：

∵共有12种等可能的结果，选中小亮A的有6种，
∴P（A）=．…（2分）

　
22．（7分）黄岩岛自古以来就是中国的领土，如图，为维护海洋利益，三沙市一艘海监船在黄岩岛附近海域巡航，某一时刻海监船在A处测得该岛上某一目标C在它的北偏东45°方向，海监船沿北偏西30°方向航行60海里后到达B处，此时测得该目标C在它的南偏东75方向，求此时该船与目标C之间的距离CB的长度，（结果保留根号）

【解答】解：由题意得：∠EBA=∠FAB=30°，
∴∠ABC=∠EBC﹣∠EBA=75°﹣30°=45°，
∴∠C=180°﹣45°﹣75°=60°；
过A作AD⊥BC于D，则BD=AD=AB•sin∠ABD=2×30×=30，
CD=，
∴CB=BD+CD=（30+10）海里．
答：该船与岛上目标C之间的距离 即CB的长度为（30+10）海里．

　
23．（9分）如图，AB是⊙O的直径，AP是⊙O的切线，点A为切点，BP与⊙O交于点C，点D是AP的中点，连结CD．
（1）求证：CD是⊙O的切线；
（2）若AB=2，∠P=30°，求阴影部分的面积．

【解答】解：（1）连结OC，AC，如图所示：

∵AB是⊙O的直径，AP是切线，
∴∠BAP=90°，∠ACP=90°，
∵点D是AP的中点，
∴DC═AP=DA，
∴∠DAC=∠DCA，
又∵OA=OC，
∴∠OAC=∠OCA，
∴∠OCD=∠OCA+∠DCA=∠OAC+∠DAC=90°，
即OC⊥CD，
∴CD是⊙O的切线；

（2）∵在Rt△ABP中，∠P=30°，
∴∠B=60°，
∴∠AOC=120°，
∴OA=1，BP=2AB=4，，
∴=．
　
24．（9分）某快餐店试销某种套餐，每份套餐的成本为5元，该店每天固定支出费用为600元（不含套餐成本）．试销一段时间后发现，若每份套餐售价不超过10元，每天可销售400份；若每份套餐售价超过10元，每提高1元，每天的销售量就减少40份．为了便于结算，每份套餐的售价x（元）取整数，用y（元）表示该店每天的利润．
（1）若每份套餐售价不超过10元．
①试写出y与x的函数关系式；
②若要使该店每天的利润不少于800元，则每份套餐的售价应为多少元？
（2）该店把每份套餐的售价提高到10元以上，每天的利润能否达到1560元？若不能，请说明理由；若能，求出每份套餐的售价应定为多少元时，既能保证利润又能吸引顾客？
【解答】解：（1）①y=400x﹣2600．（5＜x≤10）．
②依题意得：400x﹣2600≥800，解得：x≥8.5，
∵5＜x≤10，且每份套餐的售价x（元）取整数，
∴每份套餐的售价应为9元或10元．

（2）能，理由：
依题意可知：每份套餐售价提高到10元以上时，
y=（x﹣5）[400﹣40（x﹣10）]﹣600，
当y=1560时，
（x﹣5）[400﹣40（x﹣10）]﹣600=1560，
解得：x1=11，x2=14，
为了保证净收入又能吸引顾客，应取x1=11，即x2=14不符合题意．
故该套餐售价应定为11元．
　
25．（11分）（1）如图①，在四边形ABCD中，AB∥DC，E是BC的中点，若AE是∠BAD的平分线，试探究AB，AD，DC之间的等量关系，证明你的结论；
（2）如图②，在四边形ABCD中，AB∥DC，AF与DC的延长线交于点F，E是BC的中点，若AE是∠BAF的平分线，试探究AB，AF，CF之间的等量关系，证明你的结论．

【解答】解：（1）证明：延长AE交DC的延长线于点F，
∵E是BC的中点，
∴CE=BE，
∵AB∥DC，
∴∠BAE=∠F，
在△AEB和△FEC中，，[来源:学科网ZXXK]
∴△AEB≌△FEC，
∴AB=FC，
∵AE是∠BAD的平分线，
∴∠BAE=∠EAD，
∵AB∥CD，
∴∠BAE=∠F，
∴∠EAD=∠F，
∴AD=DF，
∴AD=DF=DC+CF=DC+AB，
（2）如图②，延长AE交DF的延长线于点G，
∵E是BC的中点，
∴CE=BE，
∵AB∥DC，
∴∠BAE=∠G，
在△AEB和△GEC中， ，
∴△AEB≌△GEC，
∴AB=GC，[来源:学.科.网Z.X.X.K]
∵AE是∠BAF的平分线，
∴∠BAG=∠FAG，
∵AB∥CD，
∴∠BAG=∠G，
∴∠FAG=∠G，
∴FA=FG，
∴AB=CG=AF+CF，
　
26．（13分）如图，已知抛物线y=ax2+bx+c（a≠0）与x轴交于点A（﹣1，0），B（4，0），与y轴交于点C（0，4）．
（1）求此抛物线的解析式；
（2）设点P（2，n）在此抛物线上，AP交y轴于点E，连接BE，BP，请判断△BEP的形状，并说明理由；
（3）设抛物线的对称轴交x轴于点D，在线段BC上是否存在点Q，使得△DBQ成为等腰直角三角形？若存在，求出点Q的坐标；若不存在，说明理由．

【解答】解：（1）∵抛物线上A、B、C三点坐标代入抛物线解析式y=ax2+bx+c
得，，
解得，
∴抛物线的解析式为y=﹣x2+3x+4．
（2）结论：△BEP为等腰直角三角形，理由如下：
∵点P（2，n）在此抛物线上，
∴n=﹣4+6+4=6，
∴P点坐标为（2，6）．
设直线AP解析式为y=kx+b，
把A、P两点坐标代入可得，
解得，，
∴直线AP的解析式为y=2x+2，（
令x=0可得y=2，则E点坐标为（0，2）．
∵B（4，0），P（2，6），
∴BP===2，BE===2，EP===2，
∴BE2+EP2=20+20=40=BP2，且BE=EP，
∴△BEP为等腰直角三角形．
（3）存在．
∵y=﹣x2+3x+4=﹣（x﹣）2+，
∴顶点的坐标为（，），
∵OB=OC=4，∴BC=4，∠ABC=45°．
以下分两种情况：
①若BQ=DQ，BQ1⊥DQ1，∠BDQ=45°，如图，过点Q1作Q1M⊥OB，垂足为M，
∵BQ1=DQ1，BD=4﹣=，
∴BM=Q1M=，OM=4﹣=，
∴Q1的坐标为Q1（，）．
②若DQ2=BD=，DQ2⊥BD，易得BC所在的直线解析式为y=﹣x+4，
代入x=，得y=﹣+4=，
∴DQ2=BD=，∴△BDQ2是等腰直角三角形，
所以Q2的坐标为Q2（，），
综上所述，Q的坐标为Q1（，）或Q2（，）．