初中数学湘教版九年级上册3.5 相似三角形的应用表格教学设计

这是一份初中数学湘教版九年级上册3.5 相似三角形的应用表格教学设计，共5页。教案主要包含了课堂引入，应用举例，拓展提升，当堂训练，知识网络，教学反思等内容，欢迎下载使用。


课题
3.5 相似三角形的应用
授课人
教
学
目
标
知识技能
掌握和综合运用三角形相似的判定条件和性质解决实际问题．
数学思考
运用所学知识解决实际问题．
问题解决
巩固相似三角形的有关知识，提高综合运用三角形相似的判定条件和性质解决问题的能力，发展数学应用意识，加深对相似三角形的理解和认识．
情感态度
通过问题情境的设置，培养积极的进取精神，增强数学学习的自信心，实现学生之间的交流合作，体现数学知识解决实际问题的价值．
教学重点
综合运用相似三角形的判定和性质解决实际问题．
教学难点
把生活中的问题转化为数学问题，利用工具构造相似三角形模型．
授课类型
新授课
课时
教具
小镜子、标杆、皮尺等测量工具(多媒体)
教学活动
教学步骤
师生活动
设计意图
回顾
问题：请同学们回忆判定两个三角形相似的条件有哪些？
学生口答：平行于三角形一边的直线与其他两边(或两边的延长线)相交，截得的三角形与原三角形相似；两角分别相等的两个三角形相似；两边成比例且夹角相等的两个三角形相似；三边成比例的两个三角形相似．
学生回忆并回答，为本课的学习提供迁移或类比方法.
活动
一：
创设
情境
导入
新课
【课堂引入】
1.今天我们要做一节活动课，任务是利用三角形相似的有关知识，测量我校操场上旗杆的高度．你能采用什么办法？先独立思考，再小组交流.

图3－5－7
2.每个小组准备好小镜子、标杆、皮尺等测量工具．分组活动、全班交流研讨，并运用所学知识验证结论的正确性．
用源于生活的美丽图片吸引学生的注意力，激发他们的好奇心，调动学生的学习兴趣，增强感性认识，诱发学生对新知识的需求．重点让学生明白不能利用直接测量高度的方法，为本节课的学习做好铺垫.
活动
二：
实践
探究
交流新知
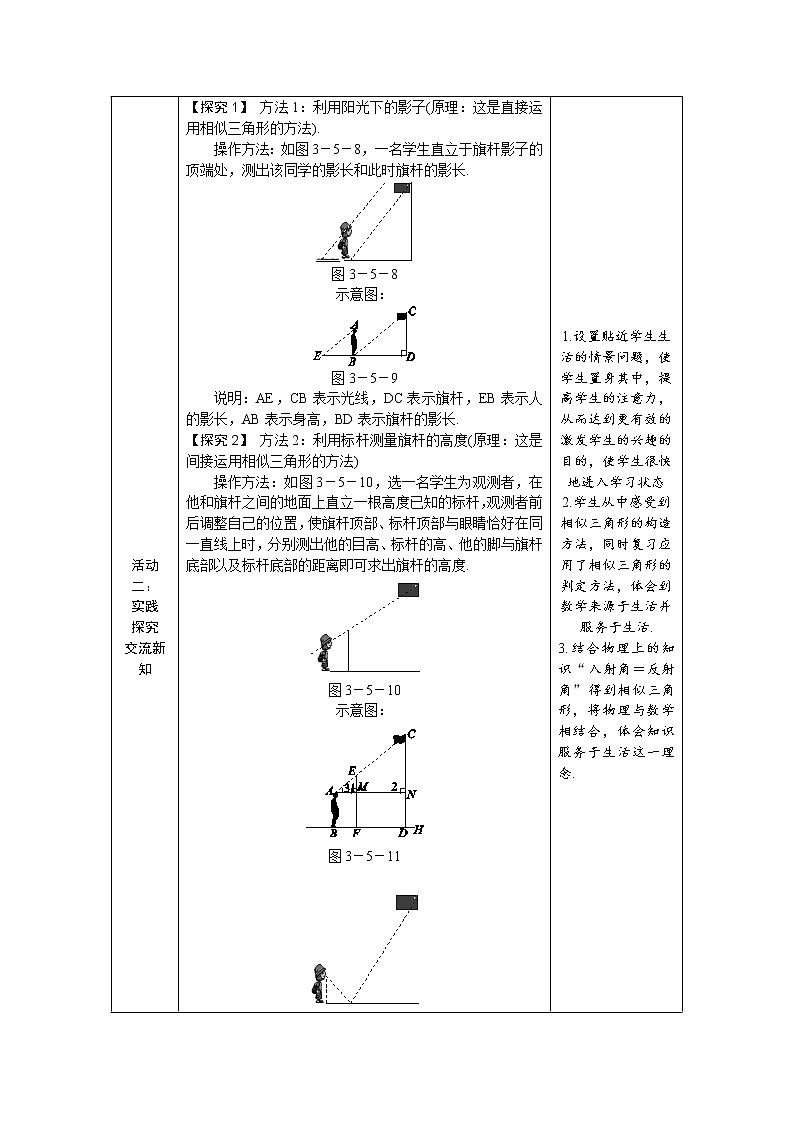
【探究1】 方法1：利用阳光下的影子(原理：这是直接运用相似三角形的方法).
操作方法：如图3－5－8，一名学生直立于旗杆影子的顶端处，测出该同学的影长和此时旗杆的影长.
图3－5－8
示意图：
图3－5－9
说明：AE，CB表示光线，DC表示旗杆，EB表示人的影长，AB表示身高，BD表示旗杆的影长.
【探究2】 方法2：利用标杆测量旗杆的高度(原理：这是间接运用相似三角形的方法)
操作方法：如图3－5－10，选一名学生为观测者，在他和旗杆之间的地面上直立一根高度已知的标杆，观测者前后调整自己的位置，使旗杆顶部、标杆顶部与眼睛恰好在同一直线上时，分别测出他的目高、标杆的高、他的脚与旗杆底部以及标杆底部的距离即可求出旗杆的高度.
图3－5－10
示意图：
图3－5－11
图3－5－12
【探究3】 方法3：利用镜子的反射(原理：这是直接运用相似三角形的方法).
操作方法：如图3－5－12，选一名学生作为观测者，在他与旗杆之间的地面上平放一面镜子，固定镜子的位置，观测者看着镜子来回调整自己的位置，使自己能够通过镜子看到旗杆顶端．测出此时他的目高、他的脚与镜子的距离、旗杆底部与镜子的距离就能求出旗杆的高度．
1.设置贴近学生生活的情景问题，使学生置身其中，提高学生的注意力，从而达到更有效的激发学生的兴趣的目的，使学生很快地进入学习状态
2.学生从中感受到相似三角形的构造方法，同时复习应用了相似三角形的判定方法，体会到数学来源于生活并服务于生活.
3.结合物理上的知识“入射角＝反射角”得到相似三角形，将物理与数学相结合，体会知识服务于生活这一理念.
活动
三：
开放
训练
体现
应用
【应用举例】
例1 [教材P92例] 在用步枪瞄准靶心时，要使眼睛(O)、准星(A)、靶心点(B)在同一条直线上．在射击时，李明由于有轻微的抖动，致使准星A偏离到A′，如图3－5－13所示．已知OA＝0.2 m，OB＝50 m，AA′＝0.0005 m，求李明射击到的点B′偏离靶心点B的长度BB′(近似地认为AA′∥BB′).
图3－5－13
变式一 已知高4 m的旗杆在水平地面上的影子长为6 m，此时测得附近一个建筑物的影子长为24 m，求该建筑物的高度.
图3－5－14 图3－5－15
变式二 明明想用镜子测量一棵古松树的高，但因树旁有一条小河，不能测量镜子与树之间的距离，于是他两次利用镜子，如图3－5－15，第一次他把镜子放在C点，人在F点正好从镜中看到树尖A；第二次他把镜子放在C′处，人在F′处正好看到树尖A.已知明明眼睛距地面1.70 m，量得CC′为12 m，CF为1.8 m，C′F′为3.84 m，求这棵古松树的高度．
运用相似三角形的周长比等于相似比，面积比等于相似比的平方求出边长和三角形的面积，再把面积转化为所需的条件，考查了学生综合运用知识的能力.
【拓展提升】
1.利用太阳光求物体的高度
例2 如图3－5－16，AB表示一个窗户的高，AM和BN表示射入室内的光线，窗户的下端到地面的距离BC＝1米，已知某一时刻BC在地面的影长CN＝1.5米，AC在地面的影长CM＝4.5米，求窗户的高度.
图3－5－16

图3－5－17
2.运用平面镜反射求物体的高度
例3 如图3－5－17是小明设计用手电筒测量某建筑物高度的示意图，点P处放一水平的平面镜，光线从点A出发经平面镜反射后刚好射到该建筑物CD的顶端C处，已知AB⊥BD，CD⊥BD，且测得AB＝1.2米，BP＝1.8米，PD＝12米，那么该建筑物的高度是多少米？
3.测量建筑物的高度
例4 如图3－5－18，亮亮蹲在地上，颖颖站在亮亮和楼之间，两人适当调整自己的位置，当楼的顶部M、颖颖的头顶B及亮亮的眼睛A恰在一条直线上时，两人分别标定自己的位置C，D，然后测出两人之间的距离CD＝1.25 m，颖颖与楼之间的距离DN＝30 m，颖颖的身高BD＝1.6 m，亮亮蹲地观测时眼睛到地面的距离AC＝0.8 m．你能根据以上测量数据帮助他们求出该住宅楼的高度吗？
图3－5－18
1.学以致用，当堂检测，及时获知学生对所学知识的掌握情况，并最大限度地调动全体学生学习数学的积极性，使每个学生都能有所收获、有所提高，明确哪些学生需要在课后加强辅导，达到全面提高的目的.
2.注重知识的直接应用，通过练习，巩固对本节课知识的理解，更好地应用相似三角形的有关知识解决相关问题.
活动
四：
课堂
总结
反思
【当堂训练】
1.教材P92练习中的T1，T2.
2.教材P93习题3.5中的T1，T2，T3.
当堂检测，及时反馈学习效果.
【知识网络】
eq \x(利用太阳光下的影子测物高)
eq \x(相似的应用) eq \x(利用标杆测物高)
eq \x(利用平面镜反射测物高)
提纲挈领，重点突出.
【教学反思】
①[授课流程反思]
通过复习回顾，创设情境引入等逐步调动学生的积极性，让学生感受数学来源于生活，反过来又为生产生活服务．通过身边问题的提出，唤起学生学习的兴趣，让学生在轻松愉快的氛围中自然地、水到渠成地掌握利用相似三角形测物高的方法.
②[讲授效果反思]
本课以活动课的方式学习，先集中讨论、确定测量方案，后分散实际操作，最后再集中总结交流．全程以学生为主体，以活动为手段，以能力提高为目的．在教学前和教学过程中充分设想学生在探究测量原理和实际测量时可能出现和遇到的问题及需要注意的事项，并给予详细的解答．在探究测量方法的过程中，尊重学生的自我发现，通过合作探究、感悟知识，得出结论．分层次设置问题，为学生展现才华提供机会.
③[师生互动反思]
______________________________________________________________________________________________
④[习题反思]
______________________________________________________________________________________________
反思，更进一步提升.