江苏省泰州中学2021-2022学年高三上学期第一次月度检测数学试题

江苏省泰州中学2021-2022学年度高三上学期第一次月度检测

数学学科试卷

命题人：     2021.10.12

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1．已知集合，，则                           （    ）

    A．    B．  C． D．

2．已知复数满足，则的共轭复数的虚部为                     （    ）

    A．    B．  C． D．

3．已知扇形的周长是4 cm，则扇形面积最大时，扇形的中心角的弧度数是      （    ）

    A．1    B．  C． 2 D．3

4． 已知为单位向量，且，则夹角的余弦值为         （    ）

A．           B．            C．              D．

5．已知函数定义域为为常数，则“”是“为在上最大值”的                                                                      （    ）

    A．充分不必要条件 B．必要不充分条件

    C．充要条件 D．既不充分也不必要条件

6．文化和旅游部在2021年围绕“重温红色历史、传承奋斗精神”、“走进大国重器、感受中国力量”、“体验美丽乡村、助力乡村振兴”这三个主题，遴选出“建党百年红色旅游百条精品线路”．这些精品线路中包含中共一大会址、嘉兴南湖、井冈山、延安、西柏坡5个传统红色旅游景区，还有港珠澳大桥、北京大兴国际机场2个展现改革开放和新时代发展成就的景区，中国天眼、“两弹一星”纪念馆、湖南十八洞村、浙江余村、贵州花茂村5个展示科技强国和脱贫攻坚成果的景区．为安排旅游路线，从上述12个景区中选3个景区，则必须含有传统红色旅游景区以及展示科技强国和脱贫攻坚成果景区的不同选法种数为       （    ）

    A．220    B．50  C．150 D．100

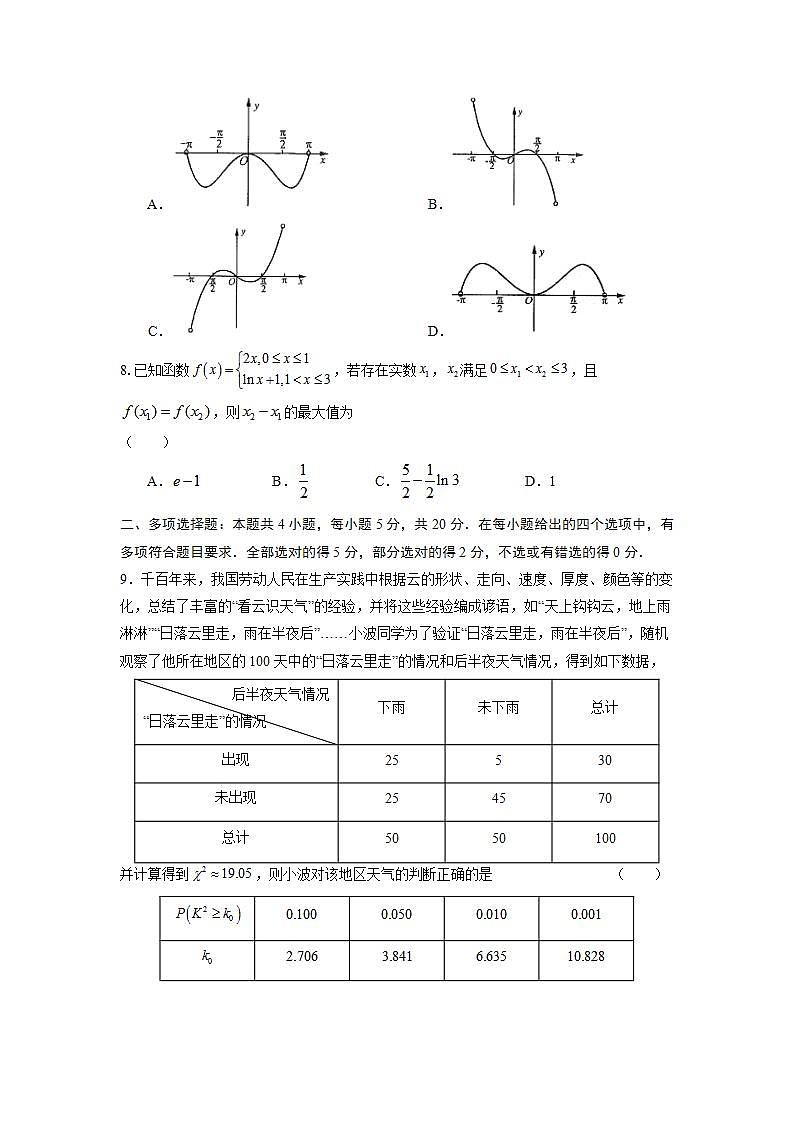
7． 函数在的图象大致为                          （    ）

    A． B．

    C． D．

8.已知函数，若存在实数，满足，且，则的最大值为                                                     （    ）

   A．          B．         C．         D．1   

二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，不选或有错选的得0分．

9．千百年来，我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等的变化，总结了丰富的“看云识天气”的经验，并将这些经验编成谚语，如“天上钩钩云，地上雨淋淋”“日落云里走，雨在半夜后”……小波同学为了验证“日落云里走，雨在半夜后”，随机观察了他所在地区的100天中的“日落云里走”的情况和后半夜天气情况，得到如下数据，

并计算得到，则小波对该地区天气的判断正确的是                 （    ）

A．后半夜下雨的概率约为

B．未出现“日落云里走”时，后半夜下雨的概率约为

C．有99%的把握认为“‘日落云里走’是否出现”与“后半夜是否下雨”有关

D．若出现“日落云里走”，则后半夜有99%的可能会下雨

10．已知，则                                             （    ）

A．的展开式中的常数项是56

B．的展开式中的各项系数之和为0

C．的展开式中的二项式系数最大值是70

D．的展开式中不含的项

11．将函数f (x)＝cos－1的图象向左平移个单位长度，再向上平移1个单位长度，得到函数g(x)的图象，则函数g(x)具有以下哪些性质                    （    ）

A．最大值为，图象关于直线x＝－对称        

B．图象关于y轴对称

C．最小正周期为π                       

D．图象关于点成中心对称

12．对函数进行研究后，得出以下结论，其中正确的有          （    ）

A．函数的图象关于y轴对称

B．

C．函数的图象与轴有无穷多个交点，且每相邻两交点间距离相等

D．对任意常数，存在常数，使函数在上单调递减，且

三､ 填空题：本题共4小题，每小题5分，共20分.

14．已知函数的定义域为R,是奇函数且,则函数的周期为________.

15. 在中，点是线段上任意一点（不包含端点），若，则的最小值是________.

16．在数列中，，为的前项和.关于的方程有唯一的解.则________；若不等式对任意的恒成立，则实数的取值范围为________.

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

17．

（1）求的最小正周期；

（2）求的单调减区间；

（3）求在区间上的最大值．

18．在中，内角的对边分别为，且.

（1）求角的大小；

（2）①，②，③以上三个条件任选两个，求边，角.

19．年月日，中国向世界庄严宣告，中国脱贫攻坚战取得了全面胜利，现行标准下万农村贫困人口全部脱贫，个贫困县全部摘帽，万个贫困村全部出列，区域性整体贫困得到解决，完成了消除绝对贫困的艰巨任务，困扰中华民族几千年的绝对贫困问题得到了历史性的解决！为了巩固脱贫成果，某农科所实地考察，研究发现某脱贫村适合种植、两种经济作物，可以通过种植这两种经济作物巩固脱贫成果，通过大量考察研究得到如下统计数据：经济作物的亩产量约为公斤，其收购价格处于上涨趋势，最近五年的价格如下表：

经济作物的收购价格始终为元/公斤，其亩产量的频率分布直方图如下：

（1）若经济作物的单价（单位：元/公斤）与年份编号具有线性相关关系，请求出关于的回归直线方程，并估计年经济作物的单价；

（2）用上述频率分布直方图估计经济作物的平均亩产量（每组数据以区间的中点值为代表），若不考虑其他因素，试判断年该村应种植经济作物还是经济作物？并说明理由．

附：，．

20．数列中，，，设．

（1）求证数列为等比数列；

（2）求数列的前项和；

（3）若，为数列的前项和，求不超过的最大的整数．

21．正态分布有极其广泛的实际背景，生产与科学实验中很多随机变量的概率分布都可以近似地用正态分布来描述.例如，同一种生物体的身长、体重等指标.随着“绿水青山就是金山银山”的观念不断的深入人心，环保工作快速推进，很多地方的环境出现了可喜的变化.为了调查某水库的环境保护情况，在水库中随机捕捞了100条鱼称重.经整理分析后发现，鱼的重量x（单位：kg）近似服从正态分布，如图所示，

（1）若从水库中随机捕捞一条鱼，求鱼的重量在内的概率；

（2）①从捕捞的100条鱼中随机挑出6条鱼测量体重，6条鱼的重量情况如表.

为了进一步了解鱼的生理指标情况，从6条鱼中随机选出3条，记随机选出的3条鱼中体重在内的条数为X，求随机变量X的分布列和数学期望；

②若将选剩下的94条鱼称重做标记后立即放生.两周后又随机捕捞1000条鱼，发现其中带有标记的有2条.为了调整生态结构，促进种群的优化，预备捕捞体重在内的鱼的总数的40%进行出售，试估算水库中鱼的条数以及应捕捞体重在内的鱼的条数.

22．定义：函数，的定义域的交集为，，若对任意的，都存在，使得，，成等比数列，，，成等差数列，那么我们称，为一对“函数”，已知函数，，．

（1）求函数的单调区间；

（2）求证：；

（3）若，对任意的，，为一对“函数”，求证：．

（为自然对数的底数）

江苏省泰州中学2021-2022学年度高三上学期第一次月度检测

数学学科参考答案

一、二、选择题：

三､ 填空题：本题共4小题，每小题5分，共20分.

13.     14.  6     15.  9    16.                  

四、解答题：本题共6小题，共70分．

17．【答案】（1）π；（2）单调递减区间为[kπ+，kπ+]，k∈Z；（3）．

解：（1）由f(x)＝2sinx（cosx﹣sinx）+1＝2sinxcosx﹣2sin²x+1＝sin2x+cos2x＝sin（2x+），

T＝＝π，所以f(x)的最小正周期为π．

（2）由2kπ+≤2x+≤2kπ+，k∈Z，

解得kπ+≤x≤kπ+，k∈Z，

所以f(x)的单调递减区间为[kπ+，kπ+]，k∈Z．

（3）因为x∈[﹣，]，所以2x∈[﹣，]，

所以2x+∈[0，π]，

当2x+＝，即x＝时，f(x)在区间[﹣，]上的最大值为．

18．【答案】（1）；（2）见详解；

解：（1）因为在中，内角，，的对边分别为，，，

所以，

由正弦定理，可将化为，

则，即，所以；

（2）若选①②，由可得，

因为，由余弦定理可得，

则，解得，

若选①③，由正弦定理可得，，则，所以，则；

因此；

若选②③，由可得，因为，所以，

19．【答案】（1），元/公斤；（2）应该种植经济作物；理由见解析．

解：（1），

，

．

则关于的回归直线方程为．

当时，，

即估计年经济作物的单价为元/公斤．

（2）利用频率和为得：

，

所以．

经济作物的亩产量的平均值为：，

故经济作物亩产值为元，

经济作物亩产值为元．

，

应该种植经济作物．

20．【答案】（1）证明见解析 ；（2） ；（3） 2021．

（1）证明：将两边都加，得，而，

即有，又，则，，

所以数列是首项为，公比为的等比数列；

（2）解：由（1）知，则，

，

，

因此，，

所以；

（3）解：由（2）知，于是得，则，

因此，，

所以不超过的最大的整数是2021．

21．【答案】（1）0.22；（2）①分布列见解析，1.5；②47000，4136.

解：（1）由正态分布的对称性可知，

（2）①随机变量X的所有可能取值为0，1，2，3，

；

；

；

，

所以X的分布列为

数学期望.

②设水库中共有N条鱼，根据题意有

则（条），

所以估计水库中有47000条鱼.

由（1）可知

则体重在内的鱼应捕捞（条）

22．【答案】（1）在上递减，在上递增；（2）证明见解析；（3）证明见解析.

（1）解：，

当时，；当时，，

∴在上递减，在上递增．

（2）证明：由（1）得，

要证，即证， 

设函数，，

当时，，当时，，

故在为减函数，在上为增函数，

故，即恒成立，

所以，

综上，．

（3）证明：由题设，对任意，存在，

使得，且，

而，

故.

法一：由（2）得，

∴．

令，则，

令，，

∴在上递增，在上递减，

又，，，

由零点存在性定理得存在（），使得，

故不等式的解为．

故，证毕．

法二：由均值不等式得．

故，

令，则，

同法一，有不等式的解为．

故，证毕．