高中数学沪教版高中二年级 第二学期12.1曲线和方程图文ppt课件

这是一份高中数学沪教版高中二年级 第二学期12.1曲线和方程图文ppt课件，共15页。PPT课件主要包含了曲线和方程，ax+by+c0，回顾直线与方程，圆的描述，代数表示，语言叙述，整理得，用集合的关系来理解，运用反例揭示内涵，满足条件1等内容，欢迎下载使用。
若二元方程ax+by+c=0(a,b不全为0）与直线l满足以下两个关系:
(1)直线l上的点的坐标都是方程ax+by+c=0(a,b不全为0）的解；（即：直线l上的点都满足方程ax+by+c=0(a,b不全为0） ）(2)以方程ax+by+c=0(a,b不全为0）的解为坐标的点都在直线l上.
那么这个方程ax+by+c=0(a,b不全为0）就叫做这条直线l的方程;这条直线l就叫做这个方程ax+by+c=0(a,b不全为0）的直线.
在描述曲线所满足的某种性质时，我们也可用方程来表示文字叙述，如：
到某一定点的距离等于定值
(1)以方程(1)的任意一组解(x,y)为坐标的点都满足“到定点A的距离为r”
(2)反之，满足“到定点A的距离为r”的点的坐标都满足方程（1）
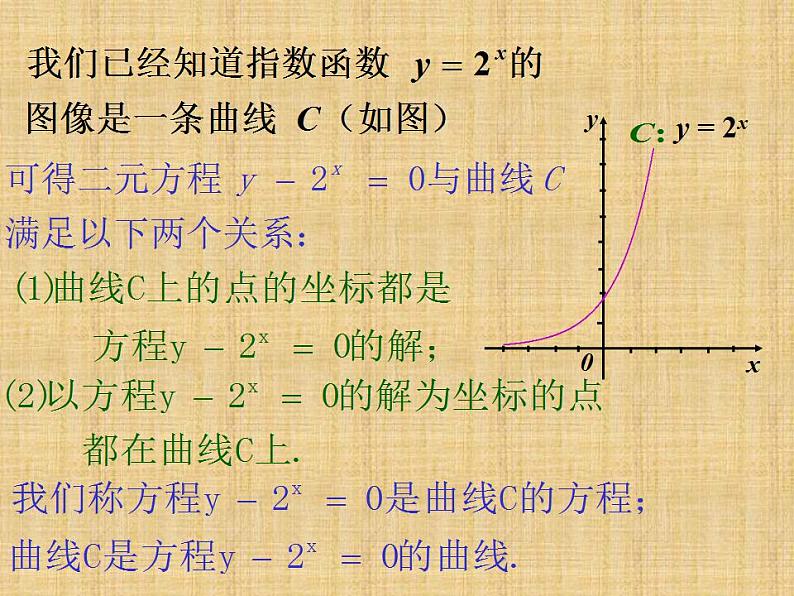
直角坐标系中，如果某曲线C上的点与一个方程F(x,y)=0的实数解建立了如下的关系： ①曲线C上的点的坐标,都是方程F(x,y)=0的解; ②以方程F(x,y)=0的解为坐标的点,都是曲线C上的点。 那么,方程F(x,y)=0叫做曲线C的方程，曲线C叫做方程F(x,y)=0的曲线。
曲线的方程与方程的曲线定义
注:(1)两个条件缺一不可;
(2)两个结论同时成立.
如果曲线C上任意一点的坐标都是方程F（x,y)=0的解，那么下列命题正确的是（ ）（A）曲线C的方程是F（x，y）=0；（B）曲线C上的点都在方程F（x，y）=0的曲线上；（C）方程F（x，y）=0的曲线是C；（D）以方程F（x，y）=0的解为坐标的点 都在曲线C上.
下述方程分别表示图1曲线吗？为什么？
例1   证明以坐标原点为圆心，半径等于5的圆O的方程是x2 +y2 = 25,并判断点A(3，-4)，B(-3，2)是否在这个圆上.
根据曲线方程的定义，由（1）、（2）可知， x2 +y2 = 25是以坐标原点为圆心，半径等于5的圆的方程.
第一步，设M1 (x1,y1)是曲线C上任一点，证明(x1,y1)是f(x,y)=0的解；
归纳: (一) 证明已知曲线的方程的方法和步骤
第二步，设(x2,y2)是F(x,y)=0的任意一个解，证明点M2 (x2,y2)在曲线C上.
(二)要判断点是否在曲线上，只要看其坐标是否满足曲线的方程即可。
如果曲线C的方程是f(x,y)=0,那么点P(x0,y0)在曲线C上的充要条件是f(x0,y0)=0
例2 求证：到两坐标轴距离相等的点的轨迹C的方程不是x-y=0.
直角坐标系中，如果某曲线C上的点与一个二元方程F(x,y)=0的实数解建立了如下的关系： ①曲线C上的点的坐标,都是方程F(x,y)=0的解; ②以方程F(x,y)=0的解为坐标的点,都是曲线C上的点。 那么,方程F(x,y)=0叫做曲线C的方程，曲线C叫做方程F(x,y)=0的曲线。
(2)两个结论同时成立。