高二数学上学期开学考试试题含答案1

高二上学期开学考试

数学试题

一、选择题：

1、     设mR，复数z=m²-1+（m-1）i 表示纯虚数，则m的值为（     ）

1. 1                 B.  -1                 C.                 D. 0

2、若向量a，b 满足=3，a⋅（b-a）= --1，则a与b的夹角为（    ）

1. 30°                B.45°                    C.60°                 D.90°

3．某企业开展“学党史庆建党周年”活动，为了解该企业员工对党史的学习情况，对该企业员工进行问卷调查，已知他们的得分都处在四个区间内，根据调查结果得到如下统计图.已知该企业男员工占，则下列结论正确的是（ ）

A．男、女员工得分在区间的占比相同

B．在各得分区间男员工的人数都多于女员工的人数

C．得分在区间的员工最多

D．得分在区间的员工占总人数的

4、已知向量a=（1 , 2），b=（2， x），且a⋅b= --1，则x 的值等于（    ）

A .                   B. -                 C.                   D. -

5、若a为实数，且  = 3 +i, 则a=(      )

1. -4                B.  -3                  C.  3                 D. 4

6．若，，，，为空间直线，，为平面，则下列说法错误的是（    ）

A．，，则

B．，，，则

C．，，，则

D．，是异面直线，则，在内的射影为两条相交直线

7、在△ABC中，cosA= ，a= ，b= ，则B等于（    ）

1. 45°或135°          B.  135°                C.  45°                D. 60°

8、设平面向量a=（1 , 2），b=（-2，y），若a∥b则=（     ）

1.                  B.                  C.                 D. 

9、已知等腰直角三角形的直角边的长为2，将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为（      ）

A. B.                 C.  π           D. π

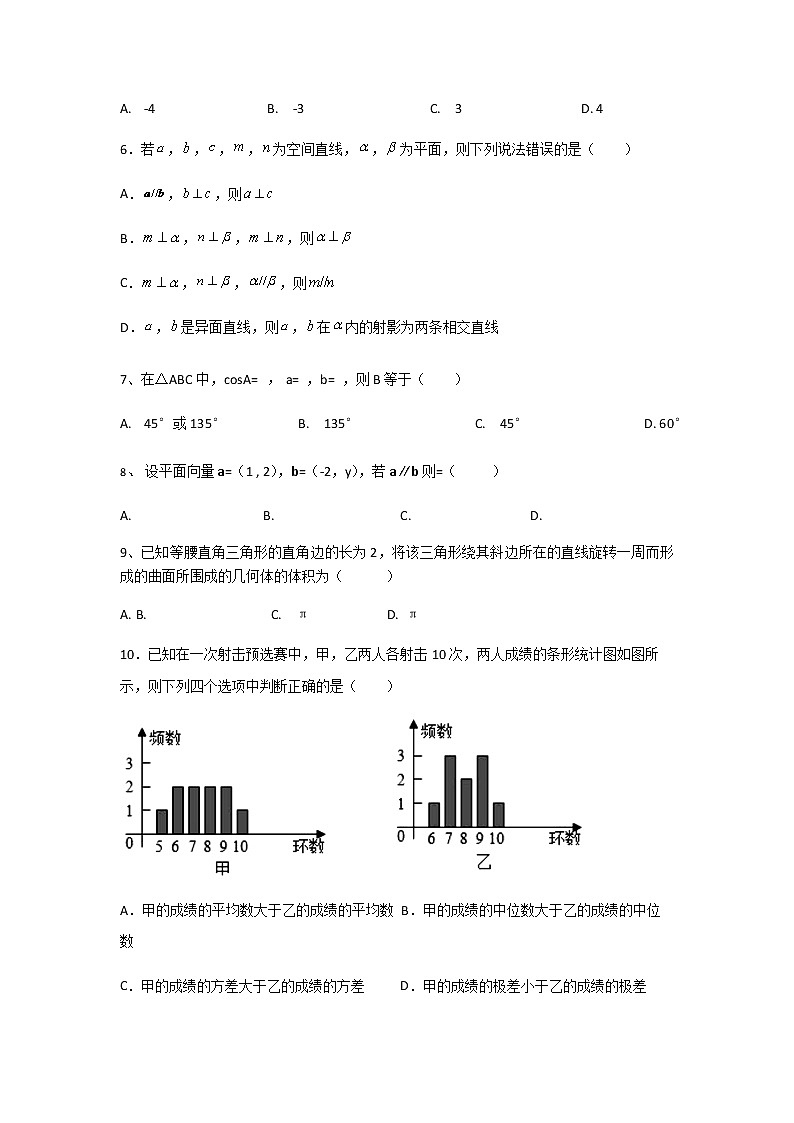
10．已知在一次射击预选赛中，甲，乙两人各射击10次，两人成绩的条形统计图如图所示，则下列四个选项中判断正确的是（    ）

A．甲的成绩的平均数大于乙的成绩的平均数 B．甲的成绩的中位数大于乙的成绩的中位数

C．甲的成绩的方差大于乙的成绩的方差     D．甲的成绩的极差小于乙的成绩的极差

11．在△ABC中，a，b，c分别为角A，B，C的对边，已知， ，且，则（    ）

A． cosB=        B．       C．  D．

12．我国古代《九章算术》中将上，下两面为平行矩形的六面体称为刍童.如图的刍童有外接球，且，，，，平面与平面间的距离为，则该刍童外接球的体积为

A． B． C． D．

二、填空题：

13、样本中有5个个体，其值分别为a，0,1,2,3，若该样本平均数为1，则样本方差为          。

14、已知H是球O的直径AB上一点，AH:HB=1:2，AB⊥平面，H为垂足，截球O所得截面的面积为π，则球O的表面积为                  。

15、一立在水平地面上的圆锥形物体的母线长为4m，一只小虫从圆锥的底面圆上的点P出发，绕圆锥表面爬行一周后回到点P处，若该小虫爬行的最短路程为m，则圆锥底面圆的半径为                。

16．在棱长为1的正方体中，为线段上的动点，

下列说法正确的是               

⑴．对任意点，平面      ⑵．三棱锥的体积为

⑶．线段长度的最小值为

⑷．存在点，使得与平面所成角的大小为

三、解答题

17．的内角的对边分别为，已知．

（1）求；

（2）若，面积为2，求．

18在直三棱柱ABC-中，∠BAC=90°，AB=AC=A.

（1）求证：A⊥平面

（2）若D为的中点，求AD与所成角的正弦值。

19．为了解某市家庭用电量的情况，该市统计局调查了100户居民去年一年的月均用电量，发现他们的用电量都在50kW·h至350kW·h之间，进行适当分组后，画出频率分布直方图如图所示．

（I）求a的值；

（Ⅱ）求被调查用户中，用电量大于250kW·h的户数；

（III）为了既满足居民的基本用电需求，又提高能源的利用效率，市政府计划采用阶梯定价，希望使80%的居民缴费在第一档（费用最低），请给出第一档用电标准（单位：kW·h）的建议，并简要说明理由．

20．在中,内角A,B,C及其所对的边a,b,c满足:C为钝角,.

(1)求证:;                (2)若,求a的取值范围.

21．在矩形ABCD中，AB＝1，BC＝2，E为AD的中点，如图1，将沿BE折起，使得点A到达点P的位置（如图2），且平面PBE⊥平面BCDE

（1）证明：PB⊥平面PEC；

（2）若M为PB的中点，N为PC的中点，求三棱锥M﹣CDN的体积.

 22．在四棱锥中，平面， AB∥DC，，，，是的中点，在线段上，且满足.

（1）求证： DE∥平面；

（2）求二面角的余弦值；

（3）在线段上是否存在点，使得与平面所成角的余弦值是，若存在，求出的长；若不存在，请说明理由.

数学答案

一．选择题：

1.B   2.C 3.A 4.D  5. D 6. D  7. C  8. A  9.B  10.C 11. D 12.C

二．填空题。

13. 2              14.            15.  m      16.⑴⑵⑶

三．解答题。

17.解：（1），∴，∵，

∴，∴，∴；

（2）由（1）可知，

∵，∴，

，

∴

．

18.

19. 解: （1）因为，所以；

（2）根据频率分布直方图可知：“用电量大于250kW·h”的频率为，

所以用电量大于250kW·h的户数为：，

故用电量大于250kW·h有户；

（3）因为前三组的频率和为：，

前四组的频率之和为，

所以频率为时对应的数据在第四组，

所以第一档用电标准为：kW·h.

故第一档用电标准为 kW·h.

20. （1）证明：由，得.

在中，因为，所以.

所以，

整理得.

因为C为钝角，所以，所以，

故.

（2）由正弦定理及（1）得.

因为，所以.

因为C为钝角，

所以，

即，

所以，所以a的取值范围为.

21.解：（1）证明：由题意，得，

∴BE2+CE2＝BC2，即BE⊥CE，

又∵平面PBE⊥平面BCDE，交线为BE，

∴CE⊥平面PBE，∴CE⊥PB，

又，

∴PB⊥平面PEC；

（2）取BE中点O，连接PO，∵PB＝PE，

∴PO⊥BE，且，

又∵平面PBE⊥平面BCDE，交线为BE，

∴PO⊥平面BCDE，

∵M为PB的中点，N为PC的中点，

 22. 解：详解：（1）证明：取的中点，的中点，连接和，

∴CD∥AB且，

∴，分别为，的中点.

且

∴且，四边形为平行四边形，

∴，平面，平面，

∴DE∥平面.

（1）由题意可得，，两两互相垂直，如果，以为原点，，，分别是，，轴建立空间直角坐标系，则，，，，

设平面的法向量为

，

∴，令∴

又，∴，∴

平面

∴∥平面

（2）设点坐标为

则，，

由得，∴

设平面的法向量为，

由得即令∴

则

又由图可知，该二面角为锐角

故二面角的余弦值为

（3）设，，∴

∴

∴

∵与平面所成角的余弦值是∴其正弦值为

∴，整理得：

，解得：，（舍）

∴存在满足条件的点，，且