2022届高三统考数学（文科）人教版一轮复习学案：8.2 空间几何体的表面积和体积

这是一份2022届高三统考数学（文科）人教版一轮复习学案：8.2 空间几何体的表面积和体积，共9页。学案主要包含了知识重温，小题热身等内容，欢迎下载使用。


【知识重温】
一、必记4个知识点
1．柱、锥、台和球的侧面积和体积
2.长方体的外接球
(1)球心：体对角线的交点．
(2)半径：r＝eq \f(\r(a2＋b2＋c2),2)(a，b，c为长方体的长、宽、高)．
3．正方体的外接球、内切球及与各条棱相切的球
(1)外接球：球心是正方体中心；半径r＝eq \f(\r(3),2)a(a为正方体的棱长)．
(2)内切球：球心是正方体中心；半径r＝eq \f(a,2)(a为正方体的棱长)．
(3)与各条棱都相切的球：球心是正方体中心；半径r＝eq \f(\r(2),2)a(a为正方体的棱长)．
4．正四面体的外接球与内切球(正四面体可以看作是正方体的一部分)
(1)外接球：球心是正四面体的中心；半径r＝eq \f(\r(6),4)a(a为正四面体的棱长)．
(2)内切球：球心是正四面体的中心；半径r＝eq \f(\r(6),12)a(a为正四面体的棱长)．
二、必明3个易误点
1．求组合体的表面积时：组合体的衔接部分的面积问题易出错．
2．由三视图计算几何体的表面积与体积时，由于几何体的还原不准确及几何体的结构特征认识不准易导致失误．
3．易混侧面积与表面积的概念．
【小题热身】
一、判断正误
1．判断下列说法是否正确(请在括号中打“√”或“×”)．
(1)圆柱的一个底面积为S，侧面展开图是一个正方形，那么这个圆柱的侧面积是2πS.( )
(2)锥体的体积等于底面面积与高之积．( )
(3)台体的体积可转化为两个锥体的体积之差．( )
(4)球的体积之比等于半径之比的平方．( )
二、教材改编
2．如图，八面体的每一个面都是正三角形，并且4个顶点A，B，C，D在同一个平面内．如果四边形ABCD是边长为30 cm的正方形，那么这个八面体的表面积为( )
A．225eq \r(3) cm2 B．1 000eq \r(3) cm2
C．1 800eq \r(3) cm2 D．900＋2 000eq \r(3) cm2
3．如图，圆柱的底面直径和高都等于球的直径，则球与圆柱的体积之比为________．
三、易错易混
4．圆柱的侧面展开图是边长为6π和4π的矩形，则圆柱的表面积为( )
A．6π(4π＋3) B．8π(3π＋1)
C．6π(4π＋3)或8π(3π＋1) D．6π(4π＋1)或8π(3π＋2)
5．《九章算术》商功章有题：一圆柱形谷仓，高1丈3尺3eq \f(1,3)寸，容纳米2 000斛(1丈＝10尺，1尺＝10寸，斛为容积单位，1斛≈1.62立方尺，π≈3)，则圆柱底面圆周长约为( )
A．1丈3尺 B．5丈4尺
C．9丈2尺 D．48丈6尺

四、走进高考
6．[2020·全国卷Ⅰ]埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥．以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为( )
A.eq \f(\r(5)－1,4) B.eq \f(\r(5)－1,2) C.eq \f(\r(5)＋1,4) D.eq \f(\r(5)＋1,2)

eq \x(考点一) 空间几何体的侧面积和表面积
[自主练透型]
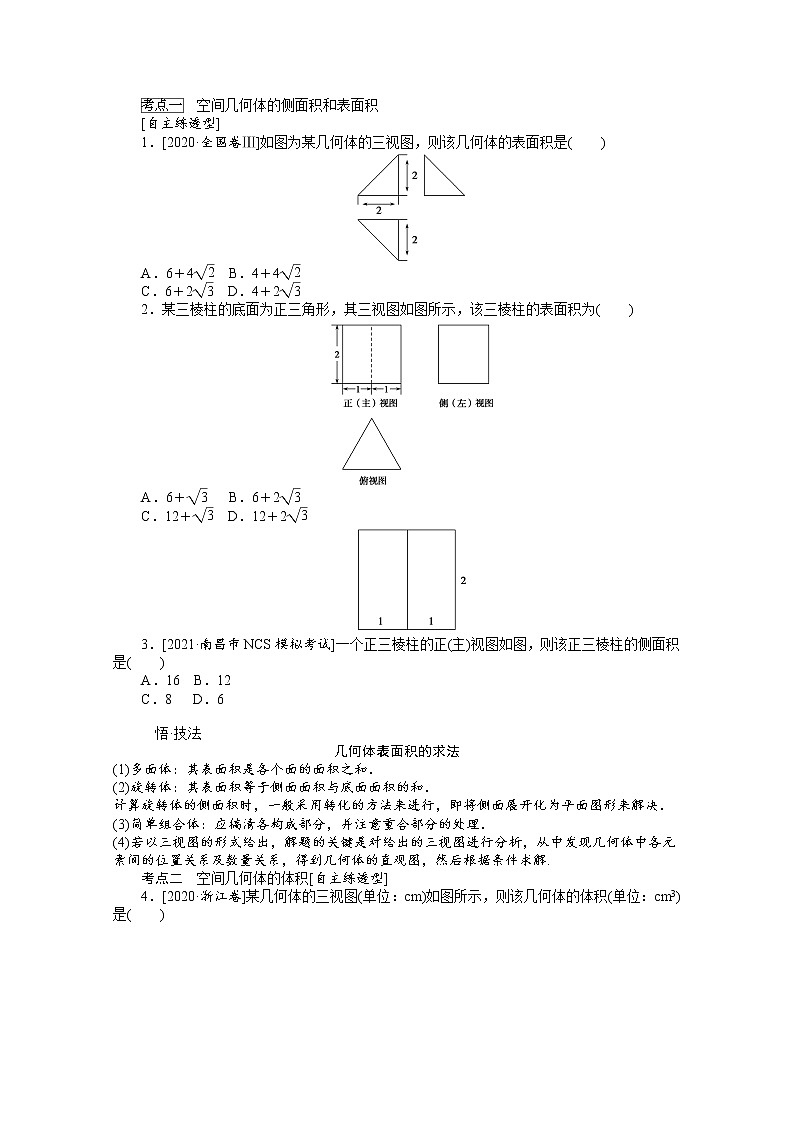
1．[2020·全国卷Ⅲ]如图为某几何体的三视图，则该几何体的表面积是( )
A．6＋4eq \r(2) B．4＋4eq \r(2)
C．6＋2eq \r(3) D．4＋2eq \r(3)
2．某三棱柱的底面为正三角形，其三视图如图所示，该三棱柱的表面积为( )
A．6＋eq \r(3) B．6＋2eq \r(3)
C．12＋eq \r(3) D．12＋2eq \r(3)
3．[2021·南昌市NCS模拟考试]一个正三棱柱的正(主)视图如图，则该正三棱柱的侧面积是( )
A．16 B．12
C．8 D．6

悟·技法
几何体表面积的求法
(1)多面体：其表面积是各个面的面积之和．
(2)旋转体：其表面积等于侧面面积与底面面积的和．
计算旋转体的侧面积时，一般采用转化的方法来进行，即将侧面展开化为平面图形来解决．
(3)简单组合体：应搞清各构成部分，并注意重合部分的处理．
(4)若以三视图的形式给出，解题的关键是对给出的三视图进行分析，从中发现几何体中各元素间的位置关系及数量关系，得到几何体的直观图，然后根据条件求解.
考点二 空间几何体的体积[自主练透型]
4．[2020·浙江卷]某几何体的三视图(单位：cm)如图所示，则该几何体的体积(单位：cm3)是( )
A.eq \f(7,3) B. eq \f(14,3)
C．3 D．6
5．[2020·江苏卷]如图，六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的．已知螺帽的底面正六边形边长为2 cm，高为2 cm，内孔半径为0.5 cm，则此六角螺帽毛坯的体积是________ cm3.
6．[2021·惠州市高三调研考试试题]某几何体的三视图如图所示，其中正视图、侧视图均是由三角形与半圆构成的，俯视图由圆与内接三角形构成，则该几何体的体积为( )
A.eq \f(\r(2)π,3)＋eq \f(1,6) B.eq \f(\r(2)π,6)＋eq \f(1,2)
C.eq \f(\r(2)π,6)＋eq \f(1,6) D.eq \f(\r(2)π,3)＋eq \f(1,2)

悟·技法
空间几何体体积的求法
(1)求简单几何体的体积．若所给的几何体为柱体、锥体或台体，则可直接利用公式求解．
(2)求组合体的体积．若所给定的几何体是组合体，不能直接利用公式求解，则常用转换法、分割法、补形法等进行求解．
(3)求以三视图为背景的几何体的体积．应先根据三视图得到几何体的直观图，然后根据条件求解.
考点三 空间几何体的外接球与内切球
[互动讲练型]
[例] (1)[2020·全国卷Ⅰ]已知A，B，C为球O的球面上的三个点，⊙O1为△ABC的外接圆．若⊙O1的面积为4π，AB＝BC＝AC＝OO1，则球O的表面积为( )
A．64π B．48π
C．36π D．32π
(2)[2020·全国卷Ⅲ]已知圆锥的底面半径为1，母线长为3，则该圆锥内半径最大的球的体积为________．
悟·技法
空间几何体与球接、切问题的求解方法
(1)求解球与棱柱、棱锥的接、切问题时，一般过球心及接、切点作截图，把空间问题转化为平面图形与圆的接、切问题，再利用平面几何知识寻找几何中元素间的关系求解．
(2)若球面上四点P，A，B，C构成的三条线段PA，PB，PC两两互相垂直，且PA＝a，PB＝b，PC＝c，一般把有关元素“补形”成为一个球内接长方体，利用4R2＝a2＋b2＋c2求解.
[变式练]——(着眼于举一反三)
1．[2021·深圳市普通高中高三年级统一考试]如图，网格纸上小正方形的边长为1，粗线画出的是某四面体的三视图，则该四面体的外接球的表面积为( )

A.eq \f(32\r(3)π,3) B．32π
C．36π D．48π
2．[2021·唐山市高三年级摸底考试]在三棱锥P－ABC中，∠BAC＝∠PBA＝∠PCA＝90°，PB＝PC＝eq \r(2)，点P到底面ABC的距离为1，则三棱锥P－ABC的外接球的表面积为( )
A．3π B.eq \f(\r(3)π,2)
C．4π D.eq \f(3π,4)



第二节 空间几何体的表面积和体积
【知识重温】
①2πrh ②Sh ③πr2h ④πrl ⑤eq \f(1,3)Sh ⑥eq \f(1,3)πr2h ⑦π(r1＋r2)l ⑧Ch ⑨Sh ⑩eq \f(1,2)Ch′ ⑪eq \f(1,3)Sh ⑫eq \f(1,2)(C＋C′)h′ ⑬4πR2 ⑭eq \x(\f(4,3)πR3)
【小题热身】
1．答案：(1)× (2)× (3)√ (4)×
2．解析：每个三角形面积为S＝eq \f(1,2)×30×15eq \r(3)＝225eq \r(3)，则表面积为S＝8×225eq \r(3)＝1 800eq \r(3)(cm2)，故选C.
答案：C
3．解析：设球的半径为R，则圆柱的底面半径为R，高为2R，
∵V球＝eq \f(4,3)πR3，V圆柱＝πR2·2R＝2πR3，
∴V球V圆柱＝eq \f(4πR3,3)2πR3＝eq \f(2,3).
答案：eq \f(2,3)
4．解析：设圆柱的底面半径为r，
分两种情况．①若6π＝2πr，r＝3，
∴圆柱的表面积为：4π×6π＋2πr2＝24π2＋18π＝6π(4π＋3)．
②若4π＝2πr，r＝2，∴圆柱的表面积为：4π×6π＋2×πr2＝24π2＋8π＝8π(3π＋1)，故选C.
答案：C
5．解析：设圆柱底面半径为r尺，高为h尺，依题意，圆柱体积为V＝πr2h＝2 000×1.62≈3×r2×13.33，所以r2≈81，即r≈9，所以圆柱底面圆周长为2πr≈54,54尺＝5丈4尺，即圆柱底面圆周长约为5丈4尺，故选B.
答案：B
6．解析：如图，设正四棱锥的底面边长BC＝a，侧面等腰三角形底边上的高PM＝h，则正四棱锥的高PO＝eq \r(h2－\f(a2,4))，
∴以|PO|为边长的正方形面积为h2－eq \f(a2,4)，
一个侧面三角形面积为eq \f(1,2)ah，
∴h2－eq \f(a2,4)＝eq \f(1,2)ah，
∴4h2－2ah－a2＝0，
两边同除以a2可得4eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(h,a)))2－2·eq \f(h,a)－1＝0，
解得eq \f(h,a)＝eq \f(1±\r(5),4)，
又∵eq \f(h,a)>0，∴eq \f(h,a)＝eq \f(\r(5)＋1,4).故选C.
答案：C
课堂考点突破
考点一
1．解析：在正方体中还原几何体如图．
几何体为正方体的一部分：三棱锥P－ABC，
S表面积＝S△PAC＋S△PAB＋S△PBC＋S△BAC
＝eq \f(1,2)×2eq \r(2)×2eq \r(2)×eq \f(\r(3),2)＋eq \f(1,2)×2×2＋eq \f(1,2)×2×2＋eq \f(1,2)×2×2＝2eq \r(3)＋6.故选C.
答案：C
2．解析：由题图知，该三棱柱为正三棱柱，且底面是边长为2的正三角形，高为2，其表面积为2×eq \f(\r(3),4)×22＋3×2×2＝12＋2eq \r(3).故选D.
答案：D
3．解析：由正(主)视图可知，该正三棱柱的底面是边长为2的正三角形，且该正三棱柱的高为2，所以该正三棱柱的侧面积为3×2×2＝12.故选B.
答案：B
考点二
4．解析：由三视图可知，该几何体是三棱柱和三棱锥的组合体，结合图中数据可得该几何体的体积V＝eq \f(1,2)×2×1×2＋eq \f(1,3)×eq \f(1,2)×2×1×1＝eq \f(7,3)(cm3)，故选A.
答案：A
5．解析：正六棱柱的体积为6×eq \f(\r(3),4)×22×2＝12eq \r(3)(cm3)，圆柱的体积为π×0.52×2＝eq \f(π,2)(cm3)，则该六角螺帽毛坯的体积为eq \b\lc\(\rc\)(\a\vs4\al\c1(12\r(3)－\f(π,2))) cm3.
答案：12eq \r(3)－eq \f(π,2)
6．解析：由三视图可知该几何体是一个半球上面有一个三棱锥，其体积V＝eq \f(1,3)×eq \f(1,2)×1×1×1＋eq \f(1,2)×eq \f(4π,3)×eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(2),2)))3＝eq \f(\r(2)π,6)＋eq \f(1,6)，故选C.
答案：C
考点三
例 解析：(1)如图，由题意知△ABC为等边三角形，圆O1的半径r＝2，即O1B＝2，∴BC＝2eq \r(3)＝OO1，
在Rt△OO1B中，OB2＝OOeq \\al(2,1)＋O1B2＝16，∴球O的半径R＝OB＝4，则S球O＝4πR2＝64π.故选A.
(2)如图为圆锥内球半径最大时的轴截面图．
其中球心为O，设其半径为r，AC＝3，O1C＝1，
∴AO1＝eq \r(AC2－O1C2)＝2eq \r(2).
∵OO1＝OM＝r，∴AO＝AO1－OO1＝2eq \r(2)－r，
又∵△AMO∽△AO1C，∴eq \f(OM,O1C)＝eq \f(AO,AC)，即eq \f(r,1)＝eq \f(2\r(2)－r,3)，故3r＝2eq \r(2)－r，∴r＝eq \f(\r(2),2).∴该圆锥内半径最大的球的体积V＝eq \f(4,3)π·eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(2),2)))3＝eq \f(\r(2)π,3).
答案：(1)A (2)eq \f(\r(2),3)π
变式练
1．解析：由三视图可知该四面体为PBCD，如图，将它补形成棱长为4的正方体，则正方体的体对角线PC就是该四面体的外接球的直径，所以外接球的直径2R＝eq \r(3×42)，所以R＝2eq \r(3)，则该四面体的外接球的表面积为4πR2＝4×π×(2eq \r(3))2＝48π，故选D.
答案：D
2．解析：通解 如图，令O为PA的中点，连接OB，OC，因为∠PBA＝∠PCA＝90°，所以OA＝OB＝OP＝OC，即O为三棱锥P－ABC的外接球的球心，又∠BAC＝90°，所以点O在底面ABC上的射影为BC的中点D，连接AD，OD，因为点P到平面ABC的距离为1，所以OD＝eq \f(1,2).因为PB＝PC＝eq \r(2)，∠PBA＝∠PCA＝90°，PA＝PA，所以△PAB≌△PAC，所以AB＝AC.令AB＝AC＝a，则PA＝eq \r(2＋a2)，BC＝eq \r(2)a，所以OA＝eq \f(\r(2＋a2),2)，AD＝eq \f(\r(2),2)a，又OD2＋AD2＝OA2，所以eq \f(1,4)＋eq \f(1,2)a2＝eq \f(2＋a2,4)，所以a＝1，所以三棱锥P－ABC的外接球的半径R＝OA＝eq \f(\r(3),2)，所以三棱锥P－ABC的外接球的表面积S＝4πR2＝3π.故选A.
优解 把三棱锥P－ABC放在正方体中，如图所示，因为点P到平面ABC的距离为1，所以正方体的棱长为1.三棱锥P－ABC的外接球即此正方体的外接球，所以三棱锥P－ABC的外接球的半径R＝eq \f(1,2)AP＝eq \f(\r(3),2)，所以三棱锥P－ABC的外接球的表面积S＝4πR2＝3π.故选A.
答案：A
面积
体积
圆柱
S侧＝①________
V＝②________＝③________
圆锥
S侧＝④________
V＝⑤________＝⑥________
＝eq \f(1,3)πr2eq \r(l2－r2)
圆台
S侧＝⑦________
V＝eq \f(1,3)(S上＋S下＋eq \r(S上S下))h
＝eq \f(1,3)π(req \\al(2,1)＋req \\al(2,2)＋r1r2)h
直棱柱
S侧＝⑧________
V＝⑨________
正棱锥
S侧＝⑩________
V＝⑪________
正棱台
S侧＝⑫________
V＝eq \f(1,3)(S上＋S下＋eq \r(S上S下))h
球
S球面＝⑬________
V＝⑭________