

2021年吉林省长春市东北师大附中高考数学五模试卷(文科)
展开2021年吉林省长春市东北师大附中高考数学五模试卷(文科)
一、单选题:本题共12小题,每小题5分,共60分。
1.(5分)已知集合A={x||x|≤2},B={x|﹣3<x<1},则A∩B=( )
A.{x|﹣3<x≤2} B.{x|﹣3≤x≤2} C.{x|﹣2≤x<1} D.{x|﹣2≤x≤1}
2.(5分)若z=,则z3=( )
A.﹣1 B.﹣i C.1 D.i
3.(5分)1750年,欧拉在给哥德巴赫的一封信中列举了多面体的一些性质,其中一条是:如果用V、E和F表示凸多面体的顶点数、棱数和面数,则有如下关系:V﹣E+F=2.已知正十二面体有20个顶点,则正十二面体有( )条棱.
A.30 B.14 C.20 D.26
4.(5分)总体由编号为01,02,…,39,40的40个个体组成.利用下面的随机数表选取5个个体,选取方法是从随机数表第1行的第6列和第7列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为( )
50 44 66 44 21 66 06 58 05 62 61 65 54 35 02 42 35 48 96 32 14 52 41 52 48
22 66 22 15 86 26 63 75 41 99 58 42 36 72 24 58 37 52 18 51 03 37 18 39 11
A.23 B.21 C.35 D.32
5.(5分)已知向量=(1,﹣1),=(2,x).若⊥(2+),则x的值为( )
A.2 B.﹣2 C.6 D.﹣6
6.(5分)已知各项均为正数的等比数列{an}的前三项和为14,且a5=3a3+4a1,则a2021=( )
A.22020 B.22021 C.22022 D.22023
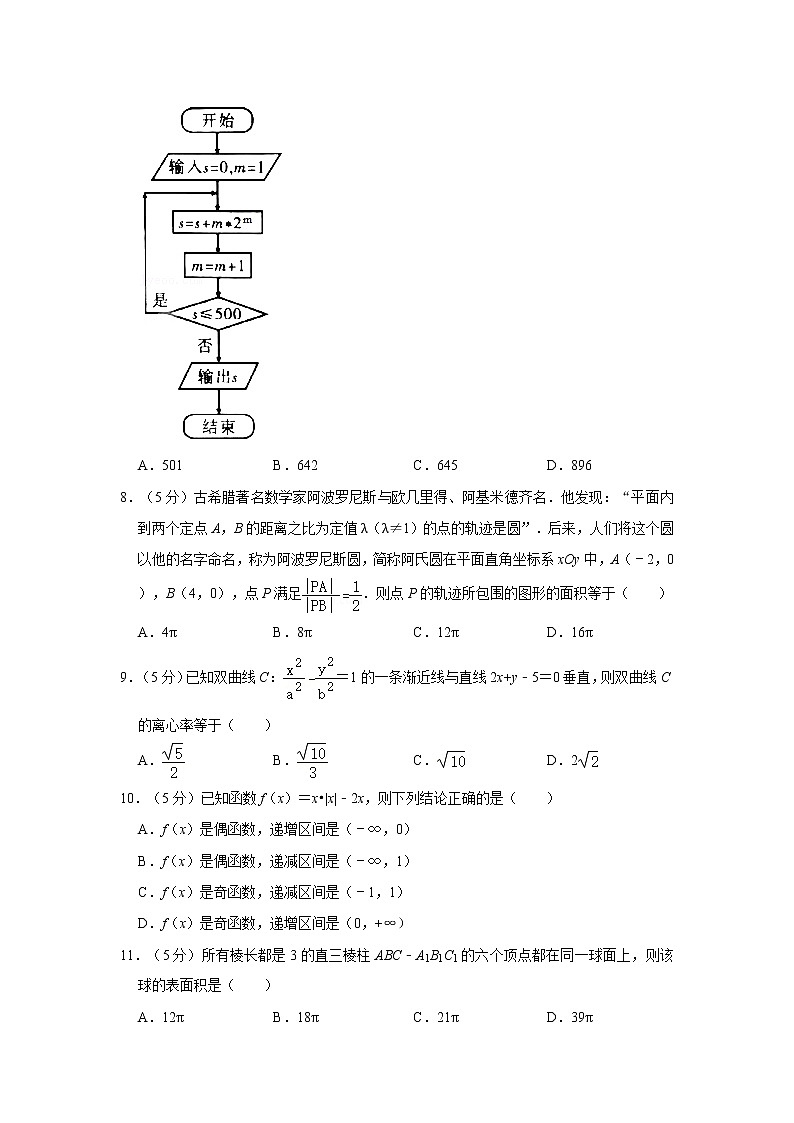
7.(5分)执行如图所示程序框图,则输出的s=( )
A.501 B.642 C.645 D.896
8.(5分)古希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名.他发现:“平面内到两个定点A,B的距离之比为定值λ(λ≠1)的点的轨迹是圆”.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆在平面直角坐标系xOy中,A(﹣2,0),B(4,0),点P满足.则点P的轨迹所包围的图形的面积等于( )
A.4π B.8π C.12π D.16π
9.(5分)已知双曲线C:=1的一条渐近线与直线2x+y﹣5=0垂直,则双曲线C的离心率等于( )
A. B. C. D.2
10.(5分)已知函数f(x)=x•|x|﹣2x,则下列结论正确的是( )
A.f(x)是偶函数,递增区间是(﹣∞,0)
B.f(x)是偶函数,递减区间是(﹣∞,1)
C.f(x)是奇函数,递减区间是(﹣1,1)
D.f(x)是奇函数,递增区间是(0,+∞)
11.(5分)所有棱长都是3的直三棱柱ABC﹣A1B1C1的六个顶点都在同一球面上,则该球的表面积是( )
A.12π B.18π C.21π D.39π
12.(5分)已知,,,则( )
A.c<b<a B.b<c<a C.a<b<c D.a<c<b
二、填空题:本题共4小题,每小题5分,共20分。
13.(5分)已知sinα=,则cos()= .
14.(5分)等差数列{an}的前n项和为Sn,若a2+a7+a12=12,则S13= .
15.(5分)设x,y满足约束条件,则目标函数的最大值是 .
16.(5分)如果三棱锥S﹣ABC的底面ABC是正三角形,顶点S在底面ABC上的射影是△ABC的中心,则这样的三棱锥称为正三棱锥,有下列结论:
①正三棱锥的所有棱长都相等;
②当三棱锥S﹣ABC所有棱长都相等时,该棱锥内任意一点P到它的四个面的距离之和为定值;
③若正三棱锥S﹣ABC的所有棱长均为2,则该棱锥内切球的半径等于;
④若正三棱锥S﹣ABC的侧棱长为2,一个侧面的顶角为40°,过点B的平面分别交侧棱SA,SC于不重合的M、N两点,则△BMN周长的最小值等于2.
以上结论正确的是 .
三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。第17-21题为必考题,每个试题考生都必须作答,共60分。第22、23题为选考题,选做一题,共10分。
17.(12分)△ABC中,角A,B,C所对的边分别为a,b,c,且bcosC+ccosB=2acosA.
(1)求角A的大小;
(2)若a=2,求△ABC面积的最大值.
18.(12分)如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,PA⊥底面ABCD,PA=AB=4,E为PB的中点,F为线段BC上的点,且BF=BC.
(1)求证:平面AEF⊥平面PBC;
(2)求点F到平面PCD的距离.
19.(12分)如图,在实验室细菌培养过程中,细菌生长主要经历调整期、指数期、稳定期和衰亡期四个时期.在一定条件下,培养基上细菌的最大承载量(达到稳定期时的细菌数量)与培养基质量具有线性相关关系.某实验室在培养细菌A的过程中,通过大量实验获得了以下统计数据:
培养基质量x(克)
20
40
50
60
80
细菌A的最大承载量Y(单位)
300
400
500
600
700
(1)建立Y关于x的回归直线方程,并预测当培养基质量为100克时细菌A的最大承载量;
(2)研究发现,细菌A的调整期一般为3小时,其在指数期的细菌数量y(单位)与细菌A被植入培养基的时间t近似满足函数关系y=0.8×2t﹣3+20,试估计在100克培养基上培养细菌A时指数期的持续时间(精确到1小时).
附注:
参考数据:210=1024,211=2048,212=4096,213=8192.
参考公式:回归方程=x中斜率和截距的最小二乘估计公式分别为:=,=﹣.
20.(12分)已知函数f(x)=lnx﹣ax(a∈R).
(1)若f(x)存在极值,求a的取值范围;
(2)当a=﹣1时,求证:f(x)≤xex﹣1.
21.(12分)已知抛物线E:y2=2px(0<p<10)的焦点为F,点M(t,8)在抛物线E上,且|FM|=10.
(1)求抛物线E的方程;
(2)过点F作互相垂直的两条直线,与抛物线分别相交于点A,B,C,D,P、Q分别为弦AB、CD的中点,求△FPQ面积的最小值.
请在22、23二题中任选一题做答,如果多做,则按所做的第一题记分.
22.(10分)在平面直角坐标系中,曲线C1的参数方程为(α为参数),以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρcos(θ+)=1.
(1)写出曲线C1的普通方程和曲线C2的直角坐标方程;
(2)已知点P(0,﹣1),曲线C1与曲线C2相交于A,B两点,求.
23.已知函数f(x)=2|x﹣1|﹣|x+1|.
(1)解不等式f(x)≥1;
(2)对∀x∈R,f(x)>m﹣|3x+3|恒成立,求m的取值范围.
2021年吉林省长春市东北师大附中高考数学五模试卷(文科)
参考答案与试题解析
一、单选题:本题共12小题,每小题5分,共60分。
1.(5分)已知集合A={x||x|≤2},B={x|﹣3<x<1},则A∩B=( )
A.{x|﹣3<x≤2} B.{x|﹣3≤x≤2} C.{x|﹣2≤x<1} D.{x|﹣2≤x≤1}
【分析】可求出集合A,然后进行交集的运算即可.
【解答】解:∵A={x|﹣2≤x≤2},B={x|﹣3<x<1},
∴A∩B={x|﹣2≤x<1}.
故选:C.
2.(5分)若z=,则z3=( )
A.﹣1 B.﹣i C.1 D.i
【分析】先化简复数z,再求出z3即可.
【解答】解:因为z====﹣i,
所以z3=(﹣i)3=i.
故选:D.
3.(5分)1750年,欧拉在给哥德巴赫的一封信中列举了多面体的一些性质,其中一条是:如果用V、E和F表示凸多面体的顶点数、棱数和面数,则有如下关系:V﹣E+F=2.已知正十二面体有20个顶点,则正十二面体有( )条棱.
A.30 B.14 C.20 D.26
【分析】根据题意,得到正十二面体中V、F的值,再由V﹣E+F=2,求出棱数E即可.
【解答】解:根据题意,正十二面体有20个顶点,即V=20,F=12,
由V﹣E+F=2,可得棱数E=V+F﹣2=30;
故选:A.
4.(5分)总体由编号为01,02,…,39,40的40个个体组成.利用下面的随机数表选取5个个体,选取方法是从随机数表第1行的第6列和第7列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为( )
50 44 66 44 21 66 06 58 05 62 61 65 54 35 02 42 35 48 96 32 14 52 41 52 48
22 66 22 15 86 26 63 75 41 99 58 42 36 72 24 58 37 52 18 51 03 37 18 39 11
A.23 B.21 C.35 D.32
【分析】根据随机数表,依次进行选择即可得到结论.
【解答】解:从随机数表第1行的第6列和第7列数字开始由左到右一次选取两个数字开始向右读,
第一个数为64,不符合条件,
第二个数为42,不符合条件,
第三个数为16,符合条件,
以下符合条件依次为:26,24,23,21,
故第5个数为21.
故选:B.
5.(5分)已知向量=(1,﹣1),=(2,x).若⊥(2+),则x的值为( )
A.2 B.﹣2 C.6 D.﹣6
【分析】根据题意,由向量的坐标计算公式可得2+的坐标,进而由向量垂直与数量积的关系可得•(2+)=4+2﹣x=0,解可得x的值,即可得答案.
【解答】解:根据题意,向量=(1,﹣1),=(2,x),则2+=(4,x﹣2),
若⊥(2+),则•(2+)=4+2﹣x=0,
解可得x=6,
故选:C.
6.(5分)已知各项均为正数的等比数列{an}的前三项和为14,且a5=3a3+4a1,则a2021=( )
A.22020 B.22021 C.22022 D.22023
【分析】由已知结合等比数列的通项公式可求a1,q,进而可求.
【解答】解:各项均为正数的等比数列{an}的前三项和=14,a5=3a3+4a1,
所以,
因为q>0,
解得q=2,a1=2,
则a2021=22021.
故选:B.
7.(5分)执行如图所示程序框图,则输出的s=( )
A.501 B.642 C.645 D.896
【分析】由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量S的值,模拟程序的运行过程,可得答案.
【解答】解:S=0,m=1,
第一次执行循环体,S=2,m=2,是;
第二次执行循环体,S=10,m=3,是;
第三次执行循环体,S=34,m=4,是;
第四次执行循环体,S=98,m=5,是;
第五次执行循环体,S=258,m=6,是;
第六次执行循环体,S=642,m=7,否;输出;
故输出S值为642,
故选:B.
8.(5分)古希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名.他发现:“平面内到两个定点A,B的距离之比为定值λ(λ≠1)的点的轨迹是圆”.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆在平面直角坐标系xOy中,A(﹣2,0),B(4,0),点P满足.则点P的轨迹所包围的图形的面积等于( )
A.4π B.8π C.12π D.16π
【分析】根据阿波罗尼斯圆的定义,即可得到点P的轨迹为圆,从可求得点P的轨迹所包围的图形的面积.
【解答】解:根据题意,设点P(x,y),则由得,
|PB|=2|PA|⇒,
化简可得,(x+4)2+y2=16,
即得点P的轨迹为以点(﹣4,0)为圆心,半径为4的圆,
故有点P的轨迹所包围的图形面积为:S=16π.
故选:D.
9.(5分)已知双曲线C:=1的一条渐近线与直线2x+y﹣5=0垂直,则双曲线C的离心率等于( )
A. B. C. D.2
【分析】求出双曲线的渐近线的斜率,然后求解离心率即可.
【解答】解:双曲线C:=1的一条渐近线与直线2x+y﹣5=0垂直,可得,
所以e===.
故选:A.
10.(5分)已知函数f(x)=x•|x|﹣2x,则下列结论正确的是( )
A.f(x)是偶函数,递增区间是(﹣∞,0)
B.f(x)是偶函数,递减区间是(﹣∞,1)
C.f(x)是奇函数,递减区间是(﹣1,1)
D.f(x)是奇函数,递增区间是(0,+∞)
【分析】根据题意,将函数的解析式写出分段函数的形式,由函数奇偶性和单调性的定义分析可得答案.
【解答】解:根据题意,f(x)=x•|x|﹣2x=,
其定义域为R,f(﹣x)=﹣(x•|x|﹣2x)=﹣f(x),
则f(x)为奇函数,
当x≥0时,f(x)=x2﹣2x=(x﹣1)2﹣1,在区间[0,1)上递减,[1,+∞)上递增,
又由f(x)为奇函数,则f(x)在区间(﹣1,0]上递减,(﹣∞,﹣1]上递增,
综合可得:f(x)的递减区间是(﹣1,1),
故选:C.
11.(5分)所有棱长都是3的直三棱柱ABC﹣A1B1C1的六个顶点都在同一球面上,则该球的表面积是( )
A.12π B.18π C.21π D.39π
【分析】正三棱柱的底面中心的连线的中点就是外接球的球心,求出球的半径即可求出球的表面积.
【解答】解:由题意可知:正三棱柱的底面中心的连线的中点就是外接球的球心,
底面中心到顶点的距离为:×3=;所以外接球的半径为:=.
所以外接球的表面积为:4π()2=21π.
故选:C.
12.(5分)已知,,,则( )
A.c<b<a B.b<c<a C.a<b<c D.a<c<b
【分析】可令f(x)=x﹣lnx,求导,根据导数符号可判断出f(x)在(0,1)上单调递减,在(1,+∞)上单调递增,然后画出图形,根据a﹣4=可得出f(a)=f(4),同理可得出f(b)=f(3),f(c)=f(2),进而可得出f(c)<f(b)<f(a),从而可得出a,b,c的大小关系.
【解答】解:令f(x)=x﹣lnx,,则f(x)在(0,1)单调递减,(1,+∞)单调递增,如图所示:
,
∴a﹣lna=4﹣ln4,
∴f(a)=f(4),
同理f(b)=f(3),f(c)=f(2),
又f(2)<f(3)<f(4),
∴f(c)<f(b)<f(a),
∴a<b<c.
故选:C.
二、填空题:本题共4小题,每小题5分,共20分。
13.(5分)已知sinα=,则cos()= ﹣ .
【分析】由已知利用诱导公式化简所求即可得解.
【解答】解:因为sinα=,
则cos()=cos(﹣α)=﹣cos(﹣α)=﹣sinα=﹣.
故答案为:﹣.
14.(5分)等差数列{an}的前n项和为Sn,若a2+a7+a12=12,则S13= 52 .
【分析】依题意可以计算出a7的值,再结合等差中项的性质代入前n项和公式即可得到所求.
【解答】解:依题意,a2+a7+a12=3a7=12,
所以a7=4,
所以S13==13a7=13×4=52,
故答案为:52.
15.(5分)设x,y满足约束条件,则目标函数的最大值是 3 .
【分析】作出不等式组对应的平面区域,利用z的几何意义,即可得到结论.
【解答】解:作出x,y满足约束条件对应的平面区域如图:
的几何意义为平面区域内的点到定点D(﹣1,0)的斜率,
由图象知AD的斜率最大,其中A(0,3),
则=3,
故答案为:3.
16.(5分)如果三棱锥S﹣ABC的底面ABC是正三角形,顶点S在底面ABC上的射影是△ABC的中心,则这样的三棱锥称为正三棱锥,有下列结论:
①正三棱锥的所有棱长都相等;
②当三棱锥S﹣ABC所有棱长都相等时,该棱锥内任意一点P到它的四个面的距离之和为定值;
③若正三棱锥S﹣ABC的所有棱长均为2,则该棱锥内切球的半径等于;
④若正三棱锥S﹣ABC的侧棱长为2,一个侧面的顶角为40°,过点B的平面分别交侧棱SA,SC于不重合的M、N两点,则△BMN周长的最小值等于2.
以上结论正确的是 ②③④ .
【分析】①由正棱锥的定义判断即可,②,③由等体积转化,求解即可,④周长的最小值,可由展开图,三点共线求解.
【解答】解:对于①,正三棱锥的侧棱长与底面边长不一定相等,故①不正确,
对于②,当三棱锥S﹣ABC所有棱长都相等时,几何体为正四面体,设三棱锥S﹣ABC的高为h,每个面的面积为S,点P到四个面的距离为d1,d2,d3,d4,
则,所以d1+d2+d3+d4=h为定值,故②正确,
对于③,因为正三棱锥所以棱长均为,设△ABC的中心为O,其外接圆半径为r,
如图,AO=r=×=,SO===,
设内切球的半径为R,∵所有棱长都相等,每个面的面积均为S,锥高h=SO,
∴由等体积可知,,解得R==,故③正确,
对于④,沿SB将正三棱锥S﹣ABC剪开,并展在一个平面内,得到其侧面展开图如图,
在侧面展开图中,当B1,N,M,B2四点共线时,原几何体中△BNM的周长最小,且为B1B2的长,
以为正三棱锥S﹣ABC的侧棱长为2,一个侧面的顶角为40°,∴SB1=SB2=2,∠B1SB2=3×40°=120°,
∴B1B2==,∴△BNM的周长最小等于,故④正确,
故答案为:②③④.
三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。第17-21题为必考题,每个试题考生都必须作答,共60分。第22、23题为选考题,选做一题,共10分。
17.(12分)△ABC中,角A,B,C所对的边分别为a,b,c,且bcosC+ccosB=2acosA.
(1)求角A的大小;
(2)若a=2,求△ABC面积的最大值.
【分析】(1)利用正弦定理将已知等式中的边化角,再结合三角形的内角和定理、两角和的正弦公式,推出cosA=,从而得解;
(2)结合余弦定理和基本不等式,可得bc≤4,再由S=bc•sinA,得解.
【解答】解:(1)由正弦定理知,=,
∵bcosC+ccosB=2acosA,
∴sinBcosC+sinCcosB=2sinAcosA,
∴sin(B+C)=sinA=2sinAcosA,
∵sinA≠0,∴cosA=,
∵A∈(0,π),∴A=.
(2)由余弦定理知,cosA=≥,
∴≥,
∴bc≤4,当且仅当b=c=2时,等号成立,
∴△ABC的面积S=bc•sinA≤×4×sin=,
故△ABC面积的最大值为.
18.(12分)如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,PA⊥底面ABCD,PA=AB=4,E为PB的中点,F为线段BC上的点,且BF=BC.
(1)求证:平面AEF⊥平面PBC;
(2)求点F到平面PCD的距离.
【分析】(1)证明BC⊥平面PAB得出AE⊥BC,结合AE⊥PB得出AE⊥平面PBC,故而平面AEF⊥平面PBC;
(2)取PD中点G,证明AG⊥平面PCD,AB∥平面PCD,则点B到平面PCD的距离为AG的长,利用BF=BC,即可求得点F到平面PCD的距离.
【解答】(1)证明:∵PA⊥平面ABCD,BC⊂平面ABCD,
∴PA⊥BC,又BC⊥AB,PA∩AB=A,
∴BC⊥平面PAB,又AE⊂面PAB,∴BC⊥AE,
∵PA=AB,E为PB中点,∴AE⊥PB,又BC∩PB=B,
∴AE⊥平面PAB,又AE⊂平面AEF,
∴平面AEF⊥平面PBC.
(2)解:∵AB∥CD,AB⊄平面PCD,CD⊂平面PCD,∴AB∥平面PCD,
∴B到平面PCD的距离等于A到平面PCD的距离,
取PD的中点G,连接AG,
∵PA⊥平面ABCD,∴PA⊥CD,
又CD⊥AD,AD∩PA=A,
∴CD⊥平面PAD,∴CD⊥AG,
∵PA=AD,G是PD的中点,∴AG⊥PD,
又PD∩CD=D,∴AG⊥平面PCD,
∵PA=AD=4,PA⊥AD,∴PD=4,
∴AG=PD=2,
∴点B到平面PCD的距离为2,
∵BF=BC,∴点F到平面PCD的距离为2×=.
19.(12分)如图,在实验室细菌培养过程中,细菌生长主要经历调整期、指数期、稳定期和衰亡期四个时期.在一定条件下,培养基上细菌的最大承载量(达到稳定期时的细菌数量)与培养基质量具有线性相关关系.某实验室在培养细菌A的过程中,通过大量实验获得了以下统计数据:
培养基质量x(克)
20
40
50
60
80
细菌A的最大承载量Y(单位)
300
400
500
600
700
(1)建立Y关于x的回归直线方程,并预测当培养基质量为100克时细菌A的最大承载量;
(2)研究发现,细菌A的调整期一般为3小时,其在指数期的细菌数量y(单位)与细菌A被植入培养基的时间t近似满足函数关系y=0.8×2t﹣3+20,试估计在100克培养基上培养细菌A时指数期的持续时间(精确到1小时).
附注:
参考数据:210=1024,211=2048,212=4096,213=8192.
参考公式:回归方程=x中斜率和截距的最小二乘估计公式分别为:=,=﹣.
【分析】(1)先求出样本中心,然后利用公式求解和,从而得到回归方程,再将x=100代入方程计算即可;
(2)利用题中给出的函数关系y=0.8×2t﹣3+20,结合(1)中的结果,列出关于t的等式,求解即可得到答案.
【解答】解:(1)由题意可得,,,
所以=20×300+40×400+50×500+60×600+80×700=139000,
=400+1600+2500+3600+6400=14500,
所以==,
故=﹣=500﹣7×50=150,
所以Y关于x的回归直线方程为=7x+150,
当培养基质量为100克时细菌A的最大承载量为=7×100+150=850(单位);
(2)在100克培养基上培养细菌A时,由(1)可知最大承载量为850单位,
又y=0.8×2t﹣3+20,即850=0.8×2t﹣3+20,化简可得2t﹣3=1037.5,
所以t﹣3≈10,则t≈13,
所以在100克培养基上培养细菌A时指数期的持续时间为10小时.
20.(12分)已知函数f(x)=lnx﹣ax(a∈R).
(1)若f(x)存在极值,求a的取值范围;
(2)当a=﹣1时,求证:f(x)≤xex﹣1.
【分析】(1)求出函数的导数,通过讨论a的范围,求出函数的单调区间,判定函数是否存在极值,从而求出a的取值范围;
(2)代入a的值,设h(x)=xex﹣lnx﹣x﹣1,定义域是(0,+∞),只需证明h(x)≥0即可,根据函数的单调性证明结论成立,
法二:问题转化为ex+lnx﹣(x+lnx)﹣1≥0,令g(x)=ex﹣x﹣1,根据函数的单调性证明即可.
【解答】解:(1)函数f(x)的定义域是(0,+∞),
f′(x)=﹣a=,当a≤0时,对任意x>0,f′(x)>0,
故函数f(x)在(0,+∞)上单调递增,f(x)无极值,
当a>0时,当x∈(0,)时,f′(x)>0,f(x)单调递增,
当x∈(,+∞)时,f′(x)<0,f(x)单调递减,
故f(x)在x=处取得极大值,无极小值,
综上:若f(x)存在极值,
则a的取值范围是(0,+∞);
(2)当a=﹣1时,xex﹣1﹣f(x)=xex﹣lnx﹣x﹣1,
设h(x)=xex﹣lnx﹣x﹣1,定义域是(0,+∞),
只需证明h(x)≥0即可,
h′(x)=(x+1)ex﹣,设u(x)=h′(x),
则u′(x)=(x+2)ex+>0,
故函数h′(x)在(0,+∞)上单调递增,
∵h′()=3(﹣1)<0,h′(1)=2e﹣2>0,
∴h′(x)=0有唯一的实根x0∈(,1)且=,
∴x0=﹣lnx0,
当0<x<x0时,h′(x)<0,当x>x0时,h′(x)>0,
故函数h(x)的最小值是h(x0),
∴h(x)≥h(x0)=x0﹣lnx0﹣x0﹣1=1+x0﹣x0﹣1=0,
∴f(x)≤xex﹣1.
法二:lnx+x≤xex﹣1,ex+lnx﹣(x+lnx)﹣1≥0,
令g(x)=ex﹣x﹣1,则g′(x)=ex﹣1,
令g′(x)>0,解得:x>0,令g′(x)<0,解得:x<0,
故g(x)在(﹣∞,0)递减,在(0,+∞)递增,
故g(x)≥g(0)=0,令h(x)=x+lnx,显然h(x)递增,
由h()<0,h(1)>0,故h(x)=0有解,x+lnx=0有解,
故ex+lnx﹣(x+lnx)﹣1≥0,(当且仅当x+lnx=0时“=”成立).
21.(12分)已知抛物线E:y2=2px(0<p<10)的焦点为F,点M(t,8)在抛物线E上,且|FM|=10.
(1)求抛物线E的方程;
(2)过点F作互相垂直的两条直线,与抛物线分别相交于点A,B,C,D,P、Q分别为弦AB、CD的中点,求△FPQ面积的最小值.
【分析】(1)由题意可知=2,所以p=4,从而得到抛物线E的方程;
(2)显然直线AB,CD的斜率都存在且均不为0,设直线AB的斜率为k,则直线CD的斜率为﹣,所以直线AB的方程为y=k(x﹣2),与椭圆方程联立,利用韦达定理得到点P的坐标,同理可得点Q的坐标,进而求出|PF|,|QF|,再利用基本不等式即可求出|PF|•|QF|的最小值,得到结果.
【解答】解:(1)抛物线E:y2=2px(0<p<10)的焦点为F,点M(t,8)在抛物线E上,且|FM|=10.
可得:,可得:p2﹣20p+64=0,因为p∈(0,10),所以p=4,
故抛物线E的方程为:y2=8x;
(2)由(1)可知焦点为F(2,0),
由已知可得AB⊥CD,所以两直线AB,CD的斜率都存在且均不为0,
设直线AB的斜率为k,则直线CD的斜率为﹣,
故直线AB的方程为y=k(x﹣2),
联立方程,消去x得:ky2﹣8y﹣16k=0,
设点A(x1,y1),B(x2,y2),则y1+y2=,
因为P(xP,yP)为弦AB的中点,所以yP=(y1+y2)=,
由yP=k(xP﹣2),得xP=+2=+2,
故点P(+2,),
同理可得:Q(4k2+2,﹣4k),
故|QF|==4,|PF|==,
所以|PF|•|QF|=4×=8×=8(|k|+)≥8×2=16,
当且仅当k=±1时,等号成立,
所以△FPQ面积的最小值16.
请在22、23二题中任选一题做答,如果多做,则按所做的第一题记分.
22.(10分)在平面直角坐标系中,曲线C1的参数方程为(α为参数),以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρcos(θ+)=1.
(1)写出曲线C1的普通方程和曲线C2的直角坐标方程;
(2)已知点P(0,﹣1),曲线C1与曲线C2相交于A,B两点,求.
【分析】(1)直接利用转换关系,在参数方程极坐标方程和直角坐标方程之间进行转换;
(2)利用一元二次方程根和系数关系式的应用求出结果.
【解答】解:(1)曲线C1的参数方程为(α为参数),转换为直角坐标方程为.
曲线C2的极坐标方程为ρcos(θ+)=1,根据转换为直角坐标方程为x﹣y﹣1=0.
(2)将直线的直角坐标方程转换为参数方程(t为参数),代入,
得到.
故,,
所以.
23.已知函数f(x)=2|x﹣1|﹣|x+1|.
(1)解不等式f(x)≥1;
(2)对∀x∈R,f(x)>m﹣|3x+3|恒成立,求m的取值范围.
【分析】(1)利用分段讨论法去掉绝对值,求不等式f(x)≥1的解集即可;
(2)问题等价于对∀x∈R,m<2|x﹣1|+2|x+1|恒成立,求出g(x)=2|x﹣1|+2|x+1|的最小值即可得出结论.
【解答】解:(1)函数f(x)=2|x﹣1|﹣|x+1|=,
不等式f(x)≥1等价于,或,或,
解得x≥4,或﹣1<x≤0,或x≤﹣1,
所以不等式f(x)≥1的解集为(﹣∞,0]∪[4,+∞);
(2)对∀x∈R,f(x)>m﹣|3x+3|恒成立,
等价于对∀x∈R,2|x﹣1|﹣|x+1|>m﹣|3x+3|恒成立,
即m<2|x﹣1|+2|x+1|恒成立,
设g(x)=2|x﹣1|+2|x+1|,x∈R,
则g(x)≥2|(x﹣1)﹣(x+1)|=2×2=4,当且仅当﹣1≤x≤1时取“=”,
所以g(x)的最小值为4,
所以m的取值范围是(﹣∞,4).
2022年吉林省长春市东北师大附中,黑龙江省大庆实验中学高考数学联考试卷(文科)(学生版+解析版): 这是一份2022年吉林省长春市东北师大附中,黑龙江省大庆实验中学高考数学联考试卷(文科)(学生版+解析版),共16页。
2022年东北三省三校(哈师大附中、东北师大附中、辽宁省实验中学)高考数学一模试卷(文科)(学生版+解析版): 这是一份2022年东北三省三校(哈师大附中、东北师大附中、辽宁省实验中学)高考数学一模试卷(文科)(学生版+解析版),共20页。
2022年东北三省三校(哈师大附中、东北师大附中、辽宁省实验中学)高考数学一模试卷(文科)(含答案): 这是一份2022年东北三省三校(哈师大附中、东北师大附中、辽宁省实验中学)高考数学一模试卷(文科)(含答案),共19页。试卷主要包含了1,则,【答案】D,【答案】C,【答案】B等内容,欢迎下载使用。












