2021届浙江省温州市高三下学期数学3月高考适应性测试试卷及答案

 高三下学期数学3月高考适应性测试试卷

一、单项选择题

1.集合 ，那么 〔    〕           

A.                   B.                   C.                   D. 

2.在平面直角坐标系中，不等式组 所表示的平面区域的面积是〔    〕           

A. 4                                           B. 2                                           C. 1                                           D. 

3. 是两个不重合的平面，直线 ，那么“ 〞是“ 〞的〔    〕           

A. 充分不必要条件           B. 必要不充分条件           C. 充分必要条件           D. 既不充分也不必要条件 

4.递增等差数列 的前 项和为 ，假设 ，且 成等比数列，那么〔    〕           

A.             B. 

            C.             D. 

5.在 中，角 所对的边分别为 ，以下条件使得 无法唯一确定的是〔    〕           

A. 
B. 

C. 
D. 

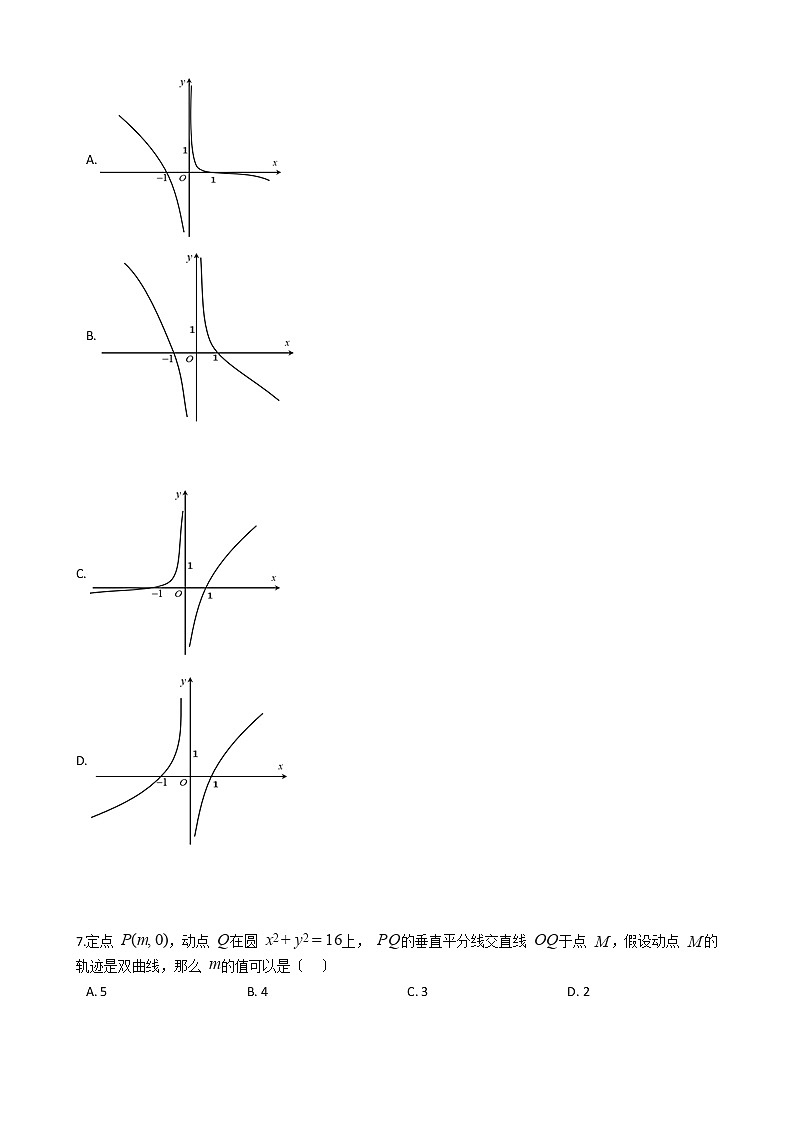
6.函数 ，那么函数 的图象可能是〔    〕           

A. 
B. 

C. 
D. 

7.定点 ，动点 在圆 上， 的垂直平分线交直线 于点 ，假设动点 的轨迹是双曲线，那么 的值可以是〔    〕           

A. 5                                           B. 4                                           C. 3                                           D. 2 

8.如图，以 为圆心，半径为1的圆始终内切于四边形 ，且 ，那么当 增大时，以下说法错误的选项是〔    〕 

A. 单调递减
B. 恒为定值 

C. 单调递增
D. 恒为非负数 

9.多项选择题给出的四个选项中会有多个选项符合题目要求．全部选对的得5分，有选错的得0分，局部选对的得3分．假设选项中有i〔其中 〕个选项符合题目要求，随机作答该题时〔至少选择一个选项〕所得的分数为随机变量 〔其中 〕，那么有〔    〕           

A.                                      B. 

C.                                      D. 

二、多项选择题

10.如图，点 分别是正四面体 棱 上的点，设 ，直线 与直线 所成的角为 ，那么〔    〕 

A. 当 时， 随着 的增大而增大 

      B. 当 时， 随着 的增大而减小 

C. 当 时， 随着 的增大而减小 

      D. 当 时， 随着 的增大而增大 

三、填空题

11. 是虚数单位，假设复数 满足 ，那么 的虚部为________； ________．   

12. ，那么 ________，假设 ，那么 ________．   

13. 、 分别是椭圆 的左、右焦点，过 的直线与椭圆交于 、 两点，假设 ，那么 ________，椭圆的离心率为________．   

14.有一种病毒在人群中传播，使人群成为三种类型：没感染病毒但可能会感染病毒的 型；感染病毒尚未康复的 型；感染病毒后康复的 型〔所有康复者都对病毒免疫〕．根据统计数据：每隔一周， 型人群中有95%仍为 型，5%成为 型； 型人群中有65%仍为 型，35%成为 型； 型人群都仍为 型．假设人口数为 的人群在病毒爆发前全部是 型，记病毒爆发 周后的 型人数为 型人数为 ，那么 ________； ________．〔用 和 表示，其中 〕   

15. 是正数，且 ，那么a+b的最小值是________．   

16.有2辆不同的红色车和2辆不同的黑色车要停放在如下列图的六个车位中的四个内，要求相同颜色的车不在同一行也不在同一列，那么共有________种不同的停放方法．〔用数字作答〕 

17.函数 ，假设对任意的 ，都存在 ，使得 ，那么实数 的最大值为________．   

四、解答题

18.如图，函数 的图象与 轴交于点 ，且 该图象的最高点． 

〔1〕求函数 在 上的零点；   

〔2〕假设函数 在 内单调递增，求正实数 的取值范围．   

19.如图，在三棱锥 中， ， ． 

〔1〕证明： ；   

〔2〕有三个条件； 

① ；

②直线 与平面 所成的角为 ；

③二面角 的余弦值为 ．

请你从中选择一个作为条件，求直线 与平面 所成的角的正弦值．

20.数列 的前 项和为 ，且 ．   

〔1〕求 及通项公式 ；   

〔2〕记 ，求数列 的前 项的和 ．   

21.如图，过点 和点 的两条平行线 和 分别交抛物线 于 和 〔其中 在 轴的上方〕， 交 轴于点 ． 

〔1〕求证：点 、点 的纵坐标乘积为定值；   

〔2〕分别记 和 的面积为 和 ，当 时，求直线 的方程．   

22.函数 ．   

〔1〕假设函数 没有极值点，求实数 的取值范围；   

〔2〕假设 对任意的 恒成立，求实数 和 所满足的关系式，并求实数 的取值范围．   

答案解析局部

一、单项选择题

1.【解析】【解答】解：因为 ，所以

所以

故答案为：B

 
【分析】首先求出集合B的补集，再根据交集的定义计算可得答案。

2.【解析】【解答】作出可行域如下列图：

不等式所表示区域即为三角形ABC  ，

由 ，求得C(0,1),

同理可求：A(1,2), B(1,0),

所以

即平面区域的面积是1.

故答案为：C

 
【分析】 先根据约束条件画出可行域，再利用几何意义求面积，只需求出区域图形的面积即可．

3.【解析】【解答】解：因为 是两个不重合的平面，直线 ，假设 ，那么存在直线 ，满足 ，因为 ，所以 ，所以 ，故充分性成立；

假设 ， ，那么 ，或 ，故必要性不成立；

所以“ 〞是“ 〞的充分不必要条件；

故答案为：A

 
【分析】 利用线面平行的性质定理，面面垂直的判定与性质定理即可判断出关系．

4.【解析】【解答】因为 是递增等差数列， ，

所以 ，即 ，①

由 成等比数列，

所以 ，整理得 ，即 ，②

①②联立求得 ，或 〔舍去〕

所以 ，

故答案为：D.

 
【分析】结合题中所给的条件，利用等差数列通项公式和求和公式以及三数成等比数列的条件，列出等量关系式，求得其首项和公差，进一步求其前10项和从而得到正确答案。

5.【解析】【解答】对于A：∵ ，∴A=140°，

由正弦定理得： ，

∴

∴ 唯一确定；A正确，不符合题意.

对于B：∵ ，

由余弦定理，可得：

由正弦定理： ，有：

可以求出角A、B  ， ∴ 唯一确定；B正确，不符合题意.

对于C：∵

由正弦定理： ，有： ，

∴ ，

∵ ∴ ∴ ,这样的角B有2个，所以 不唯一，C错误，符合题意.

对于D：∵

由正弦定理： ，有： ，

∴ ，

∵ ∴ ∴ ,这样的角A有唯一一个，

∴角C唯一，所以 唯一，D正确，不符合题意.

故答案为：C

 
【分析】 利用正弦定理，余弦定理逐项分析即可求解．

6.【解析】【解答】因为 ，

由 ，排除C D；

当 时，

，

，

又 ，

那么 ，

；

，

，

A在 减的越来越快，不符合题意；

故答案为：B.

 
【分析】 利用当-1＜x＜0时f〔x〕＜0，即可排除选项C，D，然后利用特殊值f〔e〕和f〔e2〕判断选项A，B，即可得到答案．

7.【解析】【解答】当 在圆内时，设 与圆的另一交点为 ，设点 为弦 的中点,

那么 , 线段 的中点 在线段 内，那么线段 的中垂线交线段 于点 ，如图1 .

连接 , 那么 , 所以

那么

此时 的轨迹是以 为焦点的椭圆.

当 在圆上时，线段 的中垂线交线段 于圆心 .

当 在圆外时，设 与圆的另一交点为 ，设点 为弦 的中点,

那么 , 线段 的中点 在线段 内，那么线段 的中垂线交线段 的延长线于点 ，如图2 .

连接 , 那么 , 所以

那么

此时 的轨迹是以 为焦点的双曲线的一支.

同理当 在圆上运动时，还会得到

所以动点 的轨迹是双曲线，那么 在圆外,所以

故答案为：A

 
【分析】 画出图形，结合双曲线的定义判断选项的正误即可．

8.【解析】【解答】解: 设 ，由切线长的性质得： ，

由于 ，所以 ，

所以 ，

由于 ，

所以 ，所以 ，即 ，

所以在直角三角形 中， ，即 ，所以 ，

故以 点为坐标原点， ， 所在直线为 轴建立平面直角坐标系，

那么 ， ， ， ， ，

所以 ， ， ， ，

所以当 增大时， 也在增大，

，显然单调递减，满足题意，A选项正确；

，B选项正确；

，有反比例函数易知其单调递增，C选项正确；

，由图可知 ，即 ，所以 ，D选项错误.

故答案为：D

 
【分析】 利用平面向量的数量积，结合圆内切四边形的性质逐一判断即可得解．

9.【解析】【解答】解：当 时， 的可能情况为0,3,5

选择的情况共有： 种；

， ，

所以

当 时， 的可能情况为0,3,5

选择的情况共有： 种；

， ，

所以

当 时， 的可能情况为3,5

选择的情况共有： 种；

， ，

所以

对于AB： ， ，所以 ，A不符合题意，B符合题意；

对于CD： ， ，所以 ，CD不符合题意；

故答案为：B

 
【分析】 选择情况共有情况：， 分类讨论：①i=2时，ξ2的取值为0，3，5，②i=3时，ξ3的取值为0，3，5，③i=4时，ξ4的取值为3，5，利用古典概率计算公式、相互对立事件概率计算公式即可得出概率，进而得出数学期望，即可判断出正确结论．

二、多项选择题

10.【解析】【解答】当 时，如以下列图作 交 于 点，所以直线 与直线 所成的角即为直线 与直线 所成的角，即 ，从图中可以看出，随着 的增大 逐渐增大，所以 随着 的增大而增大；

当 时，如以下列图作 交 于 点，所以直线 与直线 所成的角即为直线 与直线 所成的角，即 ，从图中可以看出，随着 的增大 逐渐减小，所以 随着 的增大而减小；

故答案为：AC.

 
【分析】 分 和 两种情况，分别过N作BC的平行线，可得直线MN与所作的平行线所成的角即为 ， 由图形分析即可得到答案.

三、填空题

11.【解析】【解答】由 ，那么

那么 的虚部为1.

故答案为：1；2

 
【分析】先由复数的除法运算化简复数  ，可得其虚部，然后再由复数的乘法运算计算求解 。

12.【解析】【解答】因为

所以令 可得

因为 ，

所以 ，所以

故答案为：1，7

 
【分析】 由， 令x=0，可得：a0；由， 可得 ，利用组合数计算公式即可得出．

13.【解析】【解答】如下列图，不妨设 ，

因为 ，所以 ，

由椭圆的定义可得 ，所以 ，

在 中，由余弦定理可得 ，

在 中，由余弦定理可

，

所以离心率 .

故答案为： ； .

 
【分析】 画出图形，设出边长，利用题意的定义以及余弦定理转化求解即可．

14.【解析】【解答】由题意，可得 ，

由①③可得 ，代入②可得 ，

那么 ，

所以数列 为等比数列，

由④可得 ，

整理得 ，

综上可得 ， .

故答案为：0.95A， .

 
【分析】由题意列出关系式，结合等比数列的定义，求得为等比数列，利用等比数列的通项公式，即可求解。

15.【解析】【解答】因为

所以

所以 ，解得 或 〔舍〕

所以a+b的最小值是8，当且仅当 时等号成立

故答案为：8

 
【分析】 根据， ， 解关于a+b的一元二次不等式，即可求得答案．

16.【解析】【解答】因为要求相同颜色的车不在同一行也不在同一列，所以第一行只能停放一辆红色车与一辆黑色车，共有 种停法,

再在第二行分类讨论停放剩下车,第二辆红车如果停在第一辆黑车下方，那么第二辆黑车有2种方法，如果第二辆红车不停在第一辆黑车下方，那么第二辆黑车有1种方法，共有3种情况，

因此共有 种情况；

故答案为：72.

 
【分析】首先在第一行停放一辆红色车与一辆黑色车，再在第二行分类讨论停放剩下车，最后利用分步计数原理即可得出结果。

17.【解析】【解答】解：当 时，取绝对值得 ，作出函数 的图像如图1，

此时， ， ，

故对任意的 ，都存在 ，使得 成立那么需满足 ，

由于 ， ，显然不满足，；

当 时，函数图像如图2所示，

此时， ， ，

故对任意的 ，都存在 ，使得 成立那么需满足 ，

由于 ， ，

所以当 时，才能满足对任意的 ，都存在 ，使得 成立，

整理不等式 得： ，解得： ，

由于 ，所以 .

由于所求为实数 的最大值，故不需要再讨论 的情况.

所以，假设对任意的 ，都存在 ，使得 ，那么实数 的最大值为1.

故答案为：1

 
【分析】 利用分段函数，通过①当时，②当时，对任意的 ，都存在 ，使得 成立那么需满足 ，即可求出实数  的最大值。

四、解答题

18.【解析】【分析】〔1〕由函数f〔x〕的图象求出A、φ和ω的值，写出f〔x〕的解析式，再求f〔x〕在[0，π]上的零点；
〔2〕求出函数y=f〔λx〕的解析式，再根据   时f〔x〕单调递增列方程求出正实数λ的取值范围．

19.【解析】【分析】〔1〕 取  中点 ， 连接 ， 证明   平面 ， 根据线面垂直的性质定理可得 ；
〔2〕分析图形 在  上取点 ，  使得 ，  以  为  轴建立空间直角坐标系 ，用向量法求线面角的正弦值，不管选 ① ② ③中哪一个，都推导出OM=OC，得出各点坐标，用向量法求解即可。

20.【解析】【分析】 〔1〕由数列递推式计算可得    ，利用 ，分别求出n为奇数和n为偶数时的通项公式，即可得解；
〔2〕分别求出n为奇数和n为偶数时数列 的通项公式，再利用等比数列前n项和公式，错位相减法求和即可求得结论。

21.【解析】【分析】〔1〕 设直线  ， 联立抛物线和直线方程，结合根与系数的关系即可求解；
〔2〕 联立方程组 ， 求得  ，根据   ，化简整理得  ， 分别联立   ， 和 ， 求得   ，结合直线的点斜式方程，即可求解。

22.【解析】【分析】 〔1〕求出原函数的导函数，因为函数  没有极值点，所以  无解或有重根，分  和  两种情况求出实数  的取值范围 ；
〔2〕 依题意得：对任意的  ，  恒成立， 令   求导得  是  的极小值，分 ，   两种情况得 函数  的图象恒在函数  图象的上方，  是函数  在  处的切线， 进而得出 当  时，对任意的  ，  恒成立 。