2020-2021学年山东省德州市高二（上）期中数学试卷人教A版

这是一份2020-2021学年山东省德州市高二（上）期中数学试卷人教A版，共8页。试卷主要包含了单项选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。


1. 抛物线y=4x2的焦点坐标为( )
A.(0, 116)B.(116, 0)C.(1,0)D.(0, 1)

2. 若构成空间的一个基底，则（ ）
A.不共面B.不共面
C.不共面D.不共面

3. 若方程x2+y2−x+y−2m＝0表示一个圆，则实数m的取值范围是（ ）
A.B.C.D.（）

4. 已知直线x+my+6＝0和(m−2)x+3y+2m＝0互相平行，则实数m的取值为（ ）
A.−1或3B.−1C.−3D.1或−3

5. 设x，y∈R，向量a→=(x,1,1)，b→=(1, y, 1)，c→=(2, −4, 2)，且a→⊥c→，b→ // c→，则|a→+b→|=( )
A.22B.10C.3D.4

6. 在平面直角坐标系xy中，已知△ABC的顶点A(−4, 0)和C(4, 0)，顶点B在椭圆x225+y29=1上，则sinA+sinCsinB等于（ ）
A.45B.52C.54D.53

7. 在一平面直角坐标系中，已知A(−1, 6)，B(2, −6)，现沿x轴将坐标平面折成60∘的二面角，则折叠后A，B两点间的距离为（ ）
A.B.C.D.

8. 对于直线xsinα+y+1=0，其倾斜角的取值范围是（ ）
A.[−π4，π4]B.[0,π2)∪[π2,π)C.[π4，3π4]D.[0,π4]∪[3π4,π)
二、多项选择题：本题共4小题，每小题5分，共20分。在每小题给出的选项中，有多项符合题目要求。全部选对的得5分，部分选对的得3分，有选错的得0分。

在四棱锥O−ABCD中，底面ABCD是边长为2的正方形，OA⊥底面ABCD，OA＝2，M，N，R分别是OA，BC，AD的中点，以下说法正确的是（ ）
A.直线MN与平面OCD的距离为
B.平面MNR与平面OCD的距离为
C.点M与平面OCD的距离为
D.点N与平面OCD的距离为

已知椭圆＝1(a>0, b>0)的左、右焦点分别F1，F2，P是椭圆上一点，若|PF1|＝3|PF2|，则椭圆的离心率可以是（ ）
A.B.C.D.

下列命题正确的是（ ）
A.已知和是两个互相垂直的单位向量，且垂直，则实数k＝−6
B.已知A(1, 1, 0)，B(0, 3, 0)，C(2, 2, 3)，则向量在上的投影向量的模长是
C.圆x2+y2＝4上有且仅有3个点到直线l:x−y+＝0的距离等于1
D.不过原点的直线都可以用方程表示

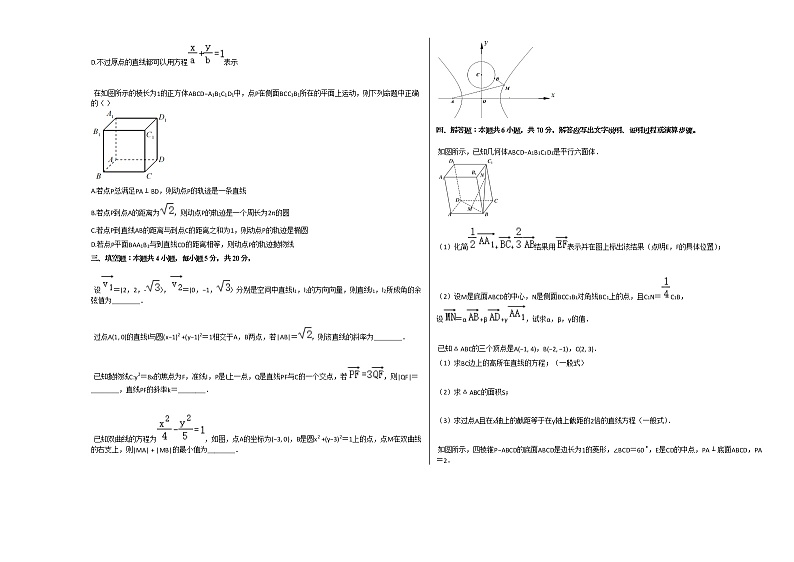
在如图所示的棱长为1的正方体ABCD−A1B1C1D1中，点P在侧面BCC1B1所在的平面上运动，则下列命题中正确的（ ）

A.若点P总满足PA⊥BD，则动点P的轨迹是一条直线
B.若点P到点A的距离为，则动点P的轨迹是一个周长为2π的圆
C.若点P到直线AB的距离与到点C的距离之和为1，则动点P的轨迹是椭圆
D.若点P平面BAA1B1与到直线CD的距离相等，则动点P的轨迹抛物线
三、填空题：本题共4小题，每小题5分，共20分，

设＝(2，2，-），＝(0，−1，）分别是空间中直线l1，l2的方向向量，则直线l1，l2所成角的余弦值为________．

过点A(1, 0)的直线l与圆(x−1)2+(y−1)2＝1相交于A，B两点，若|AB|＝，则该直线的斜率为________．

已知抛物线C:y2＝8x的焦点为F，准线l，P是l上一点，Q是直线PF与C的一个交点，若，则|QF|＝________，直线PF的斜率k＝________．

已知双曲线的方程为，如图，点A的坐标为(−3, 0)，B是圆x2+(y−3)2＝1上的点，点M在双曲线的右支上，则|MA|+|MB|的最小值为________．

四、解答题：本题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤。

如图所示，已知几何体ABCD−A1B1C1D1是平行六面体．

（1）化简++结果用表示并在图上标出该结果（点明E，F的具体位置）；

（2）设M是底面ABCD的中心，N是侧面BCC1B1对角线BC1上的点，且C1N＝C1B，
设＝α+β+γ，试求α，β，γ的值．

已知△ABC的三个顶点是A(−1, 4)，B(−2, −1)，C(2, 3)．
（1）求BC边上的高所在直线的方程；（一般式）

（2）求△ABC的面积S；

（3）求过点A且在x轴上的截距等于在y轴上截距的2倍的直线方程（一般式）．

如图所示，四棱锥P−ABCD的底面ABCD是边长为1的菱形，∠BCD＝60∘，E是CD的中点，PA⊥底面ABCD，PA＝2．

（1）证明：平面PBE⊥平面PAB；

（2）求平面PAD和平面PBE所成二面角（锐角）的正弦值．

已知F1，F2是椭圆C：(a>b>0)的两个焦点，P为C上一点．
（1）若△F1PF2为等腰直角三角形，求C的离心率；

（2）如果存在点P，使得PF1⊥PF2，且△F1PF2的面积等于9，求b的值和a的取值范围．

在四棱锥S−ABCD中，底面ABCD为长方形，SB⊥底面ABCD，其中BS＝2，BA＝2，BC＝t，t的可能取值为：①；②；③；④；⑤t＝3．

（1）求直线AS与平面ABCD所成角的正弦值；

（2）若线段CD上能找到点E，满足AE⊥SE，则t可能的取值有几种情况？请说理由；

（3）在（2）的条件下，当t为所有可能情况的最大值时，线段CD上满足AE⊥SE的点有两个，分别记为E1，E2，求二面角E1−SB−E2的大小．

已知半径为5的圆M的圆心在x轴上，圆心M的横坐标是整数，且与直线4x+3y−29＝0相切．
（1）求圆M的方程；

（2）若直线ax−y+5＝0(a≠0)与圆M相交于A，B两点，是否存在实数a，使得过点P(−2, 4)的直线l垂直平分弦AB？若存在，求出实数a的值；若不存在，请说明理由．

（3）设P(−1, 0)，若动圆N过点P且与圆M内切，求动圆圆心N的轨迹方程．
参考答案与试题解析
2020-2021学年山东省德州市高二（上）期中数学试卷
一、单项选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1.
【答案】
A
【考点】
抛物线的定义
【解析】
根据题意，将抛物线的方程变形为标准方程，分析可得其焦点位置以及p的值，有抛物线焦点坐标公式计算可得答案．
【解答】
解：∵ 抛物线的方程为y=4x2，
∴ 其标准方程为x2=14y，
∴ 2p=14，解得：p=18，
∴ 焦点坐标为(0, 116).
故选A.
2.
【答案】
A
【考点】
空间向量的基本定理及其意义
空间向量的正交分解及其坐标表示
【解析】
此题暂无解析
【解答】
此题暂无解答
3.
【答案】
C
【考点】
二元二次方程表示圆的条件
圆的一般方程
【解析】
此题暂无解析
【解答】
此题暂无解答
4.
【答案】
B
【考点】
直线的一般式方程与直线的平行关系
【解析】
两条直线x+my+6＝0和(m−2)x+3y+2m＝0互相平行，m(m−2)−3＝0，解得m．经过验证即可得出．
【解答】
两条直线x+my+6＝0和(m−2)x+3y+2m＝0互相平行，
∴ m(m−2)−3＝0，解得m＝−1，3．
经过验证，m＝3时，两条直线相互重合，舍去．
∴ m＝−1，
5.
【答案】
C
【考点】
向量的数量积判断向量的共线与垂直
向量的模
【解析】
利用向量平行和向量垂直的性质列出方程组，求出x，y，再由平面向量坐标运算法则求出a→+b→，由此能求出|a→+b→|．
【解答】
解：由题意知，x，y∈R，向量a→=(x, 1, 1)，b→=(1, y, 1)，c→=(2, −4, 2)，
且a→⊥c→，b→ // c→，
∴ 2x−4+2=0，12=y−4=12，
解得x=1，y=−2，
∴ a→+b→=(1, 1, 1)+(1, −2, 1)=(2, −1, 2)，
∴ |a→+b→|=4+1+4=3．
故选C.
6.
【答案】
C
【考点】
椭圆的定义
正弦定理的应用
【解析】
首先根据椭圆的方程可得a与b的值，进而可得c的值，分析可得，AC就是焦点，由正弦定理可得：sinA+sinCsinB=BC+BAAC；结合椭圆的定义可得AC=2c=8，BC+BA=2a=10；代入数据可得答案．
【解答】
解：根据题意，由椭圆的方程可得a=5，b=3；
则其焦点坐标为(−4, 0)和(4, 0)，恰好是A、C两点，
则AC=2c=8，BC+BA=2a=10；
由正弦定理可得：sinA+sinCsinB=BC+BAAC=54；
故选C．
7.
【答案】
【考点】
二面角的平面角及求法
点、线、面间的距离计算
【解析】
此题暂无解析
【解答】
此题暂无解答
8.
【答案】
D
【考点】
直线的倾斜角
【解析】
由直线的方程可确定直线的斜率，可得其范围，进而可求倾斜角的取值范围．
【解答】
解：直线xsinα+y+2=0的斜率为k=−sinα，
∵ |sinα|≤1，∴ |k|≤1
∴ 倾斜角的取值范围是[0, π4]∪[3π4, π)
故选：D．
二、多项选择题：本题共4小题，每小题5分，共20分。在每小题给出的选项中，有多项符合题目要求。全部选对的得5分，部分选对的得3分，有选错的得0分。
【答案】
【考点】
命题的真假判断与应用
棱锥的结构特征
点、线、面间的距离计算
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
B,C
【考点】
椭圆的离心率
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
B,C
【考点】
向量的投影
直线的两点式方程
命题的真假判断与应用
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
A,B,D
【考点】
命题的真假判断与应用
【解析】
此题暂无解析
【解答】
此题暂无解答
三、填空题：本题共4小题，每小题5分，共20分，
【答案】
【考点】
异面直线及其所成的角
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
±1
【考点】
直线与圆的位置关系
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
,
【考点】
抛物线的性质
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
3+3
【考点】
双曲线的离心率
【解析】
此题暂无解析
【解答】
此题暂无解答
四、解答题：本题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤。
【答案】
取AA1的中点E，在D1C3上取一点F，
使得D1F＝2FC3，连接EF，
则++＝++＝．
（与相等的向量都对）………
＝+＝+
＝（+）+（+）
＝++，
所以α＝，β＝． ………
【考点】
空间向量
向量的线性运算性质及几何意义
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
设BC边上的高所在直线为l，由题意知kBC＝＝1l＝＝−1．
又点A(−1, 5)在直线l上，
即x+y−3＝0，即BC边上的高所在直线的方程为x+y−4＝0．
BC边所在直线的方程为y+1＝x+6，
即x−y+1＝0．点A(−5＝2．
又|BC|＝＝4​△ABC＝•|BC|⋅d＝×2．
当直线过原点时，设直线方程为y＝kx，直线方程4x+y＝0；
当直线在坐标轴上的截距都不为4时，设直线方程为，所以直线方程为x+2y−7＝0．
所以直线方程为4x+y＝4或x+2y−7＝7．
【考点】
直线的一般式方程与直线的性质
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
证明：如图所示，连接BD，
知△ABC是等边三角形．
∵ E是CD的中点，
∴ BE⊥CD，又AB // CD，
∴ AB⊥BE，∴ BE⊥平面PAB，
又BE⊂平面PBE，
∴ 平面PBE⊥平面PAB．
在平面ABCD内，过点A作AB的垂线，以A为原点建立空间直角坐标系.，．
易知，＝(7，0，＝(0，，＝(0，6，＝（，，
设是平面PBE的一个法向量，
则由得令z7＝1，得，
设是平面PAD的一个法向量，
则由得
所以z2＝0，，故可取，
于是，
设所成锐二面角为θ，所以sinθ＝，
所以平面PAD和平面PBE所成锐二面角的正弦值为．
【考点】
二面角的平面角及求法
平面与平面垂直
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
△F1PF2为等腰直角三角形可知有三种情况．
当∠PF8F2＝90∘时，|PF1|＝6c，，
于是，
得e＝，当∠PF8F1＝90∘时，同理求得e＝；
当∠F1PF2＝90∘时，则P在椭圆短轴的端点，，
，解得e＝．
∴ C的离心率为或；
设P(x, y)1PF5的面积等于9，得•2c⋅|y|＝9，①
由PF4⊥PF2，得x2+y7＝c2，②
再由P在椭圆上，得，③
由②③及a2+b2＝c3，得y2＝，又由①知y2＝，故b＝3，
由②③得x8＝，∴ c2≥b8，从而a2＝b2+c7≥2b2＝18，故a≥7，
∴ b＝3，a≥5，
故b＝3，a得取值范围为[2．
【考点】
椭圆的离心率
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
∵ SB⊥底面ABCD，SA在平面ABCD内的射影为AB，
∴ ∠SAB即为直线AS与平面ABCD所成的角，
∴ 在Rt△SBA中，．
所以直线AS与平面ABCD所成角的正弦值．
如图所示，以B为坐标原点，BA，y轴．
则各点坐标分别为A(0, 5, 0)，0，5)，2，0)，5，2)．
设E(t, x, 0)(6≤x≤2)，，．
∵ x∈[0, 2]，t8＝x(2−x)∈[0, 8]
∴ 在所给的数据中，t可以取①②③．
由（2）知，此时，．
根据题意得，其坐标为，
∵ SB⊥底面ABCD，∴ SB⊥BE1，SB⊥BE2，
∴ ∠E5BE2是二面角E1−SB−E7的平面角，
由，
由题意得，二面角E2−SB−E2为锐角，所以二面角的大小为30∘．
【考点】
二面角的平面角及求法
直线与平面所成的角
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
设圆心坐标为M(m, 0)(m∈Z)，
由于圆与直线4x+5y−29＝0相切，且圆的半径为5，
所以＝5，即2m−29＝25或4m−29＝−25，
解得m＝或m＝5，故m＝1，
故所求的圆的方程为(x−1)6+y2＝25．
设符合条件的实数a存在，
因为a≠0，则直线l的斜率为-(x+2)+6，
即x+ay+2−4a＝6．
由于直线l垂直平分弦AB，故圆心M(1，
所以1+2+2−4a＝3，解得a＝．
经检验，当a＝时，
故存在实数a＝，使得过点P(−2．
因为圆N过点P(−1, 4)所以PN为半径，
所以MN＝5−PN即MN+PN＝5，
所以点M的轨迹是以M，P为焦点，
所以6a＝5，c＝1
所以所求轨迹方程是＝1或．
【考点】
直线与圆的位置关系
轨迹方程
【解析】
此题暂无解析
【解答】
此题暂无解答