2021年云南省红河州高考数学第三次复习统一检测试卷（文科）

这是一份2021年云南省红河州高考数学第三次复习统一检测试卷（文科），共25页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2021年云南省红河州高考数学第三次复习统一检测试卷（文科）
一、选择题：本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的.
1．（5分）已知集合A＝{x|x2﹣2x﹣3＜0，x∈N*}，B＝{﹣1，0，1，2}，则A∩B＝（　　）
A．{﹣1，0，1，2} B．{0，1，2} C．{1，2} D．{1，2，3}
2．（5分）已知复数，i为虚数单位，是z的共轭复数，则＝（　　）
A． B． C． D．
3．（5分）已知，则＝（　　）
A． B．﹣ C． D．﹣
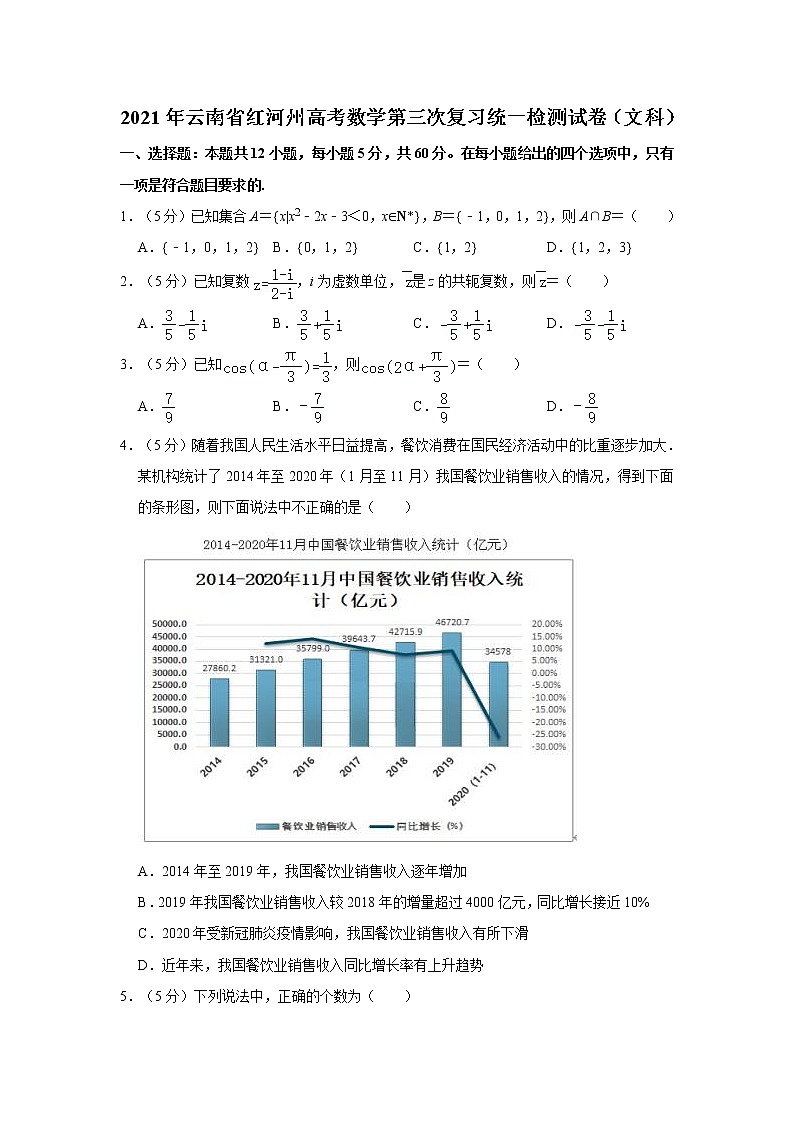
4．（5分）随着我国人民生活水平日益提高，餐饮消费在国民经济活动中的比重逐步加大．某机构统计了2014年至2020年（1月至11月）我国餐饮业销售收入的情况，得到下面的条形图，则下面说法中不正确的是（　　）

A．2014年至2019年，我国餐饮业销售收入逐年增加
B．2019年我国餐饮业销售收入较2018年的增量超过4000亿元，同比增长接近10%
C．2020年受新冠肺炎疫情影响，我国餐饮业销售收入有所下滑
D．近年来，我国餐饮业销售收入同比增长率有上升趋势
5．（5分）下列说法中，正确的个数为（　　）
①若，是非零向量，则“＞0”是“与的夹角为锐角”的充要条件；
②命题“在△ABC中，若sinA＞sinB，则A＞B”的逆否命题为真命题；
③已知命题p：，则它的否定是￢p：∀x∉R，x2+x+2＞0．
A．0 B．1 C．2 D．3
6．（5分）在三棱锥P﹣ABC中，已知PA，PB，PC两两垂直，且PA＝1，PB＝2，PC＝3，则三棱锥P﹣ABC的外接球的表面积为（　　）
A．13π B．14π C．56π D．64π
7．（5分）函数f（x）＝•cosx的图象大致是（　　）
A． B．
C． D．
8．（5分）如图所示，网格中小正方形的边长均为1，△ABC的三个顶点均在小正方形的顶点处，则△ABC外接圆的面积为（　　）

A． B． C． D．
9．（5分）已知55＞3，a＝log23，b＝log35，c＝，则（　　）
A．a＞b＞c B．c＞a＞b C．a＞c＞b D．b＞c＞a
10．（5分）已知实数x，y满足约束条件|x±y|≤2，若在该区域内随机取一点P（x，y），则该点落在所表示的曲线与x轴围成的图形内部的概率为（　　）
A． B． C． D．
11．（5分）已知数列{an}的前n项和为Sn，且满足Sn＝4n2+n（n∈N*）．若数列{bn}满足bn＝，则++…+＝（　　）
A． B． C． D．
12．（5分）已知函数f（x）是R的奇函数，且满足f（x+1）＝f（x﹣1），当x∈（0，1]，f（x）＝lnx，则下列关于函数f（x）叙述正确的是（　　）
A．函数f（x）的最小正周期为1
B．函数f（x）在（0，2021）内单调递增
C．函数f（x）相邻两个对称中心的距离为2
D．函数y＝f（x）+lnx在区间（0，2021）内有1011个零点
二、填空题：本题共4小题，每小题5分，共20分.
13．（5分）若△ABC是边长为1的等边三角形，则＝　 　．
14．（5分）函数在（﹣π，π）上的零点之和为　 　．
15．（5分）已知双曲线，过下焦点F作斜率为2的直线与双曲线的一条渐近线相交于点A，且A在第一象限，若|OA|＝|OF|（O为坐标原点），则双曲线C的离心率为　 　．
16．（5分）丹麦数学家琴生是19世纪对数学分析做出卓越贡献的巨人，特别是在函数的凹凸性与不等式方面留下了很多宝贵的成果．定义：函数f（x）在（a，b）上的导函数为f'（x），f'（x）在（a，b）上的导函数为f''（x），若在（a，b）上f''（x）＜0恒成立，则称函数f（x）是（a，b）上的“严格凸函数”，称区间（a，b）为函数f（x）的“严格凸区间”．则下列正确命题的序号为 　 　．
①函数f（x）＝﹣x3+3x2+2在（1，+∞）上为“严格凸函数”；
②函数的“严格凸区间”为；
③函数在（1，4）为“严格凸函数”，则m的取值范围为[e﹣1，+∞）．
三、解答题：共70分。解答应写出文字说明、证明过程或演算步骤。第题为必考题，每个试题考生都必须作答.第、题为选考题，考生根据要求作答.（一）必考题：共分.
17．（12分）已知公差不为0的等差数列{an}的前n项和为Sn，且S3＝9，a1，a2，a5成等比数列．
（1）求数列{an}的通项公式；
（2）若数列{bn}满足，求数列{bn﹣an}的前n项和Tn．
18．（12分）某市从2020年5月1日开始，若电子警察抓拍到机动车不礼让行人的情况后，交警部门将会对不礼让行人的驾驶员进行扣3分，罚款200元的处罚，并在媒体上曝光．但作为交通重要参与者的行人，闯红灯通行却频有发生，带来了较大的交通安全隐患和机动车通畅率降低点情况．交警部门在某十字路口根据以往的监测数据，得到行人闯红灯的概率为0.2，并从穿越该路口的行人中随机抽取了200人进行调查，对是否存在闯红灯的情况进行统计，得到2×2列联表如下：

45岁以下
45岁以上
合计
闯红灯人数

25

未闯红灯人数
85


合计


200
近期，为了整顿“行人闯红灯”这一不文明的违法行为，交警部门在该十字路口试行了对闯红灯的行人进行5元以上，50元以下的经济处罚．在试行经济处罚一段时间后，交警部门再次对穿越该路口的行人中随机抽取了200人进行调查，对是否存在闯红灯的情况进行统计，得到2×2列联表如下：

45岁以下
45岁以上
合计
闯红灯人数
5
15
20
未闯红灯人数
95
85
180
合计
100
100
200
将统计数据所得频率视为概率，完成下列问题：
（1）将2×2列联表填写完整（不需要写出填写过程），并根据表中数据分析，在试行对闯红灯的行人进行经济处罚前，是否有90%的把握认为闯红灯行为与年龄有关；
（2）在试行对闯红灯的行人进行经济处罚后，闯红灯现象是否有明显改善，请说明理由；
（3）结合调查结果，请你对“如何治理行人闯红灯现象”提出合理的建议（至少提出两条建议）．
参考公式：，其中n＝a+b+c+d．
参考数据：
P（K2≥k0）
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k0
1.132
2.072
2.706
3.841
5.024
6.635
7.879
10.828
19．（12分）如图，在四棱锥P﹣ABCD中，四边形ABCD为直角梯形，AB∥CD，AB⊥BC，AB＝BC＝2CD＝4，PA＝2，PB＝2，E为BC的中点，且PE⊥BD．
（1）证明：PA⊥平面ABCD；
（2）线段PB上是否存在一点M，使得三棱锥A﹣DEM的体积为？若存在，试确定点M的位置；若不存在，请说明理由．

20．（12分）已知抛物线C：y2＝2px（p＞0）的准线经过椭圆的一个焦点．
（1）求抛物线C的方程；
（2）过椭圆的右顶点且斜率为k1，k2的两条直线分别交抛物线C于点A，B，M，N，点P，Q分别是线段AB，MN的中点，若k1+k2＝2，求抛物线C的焦点F到直线PQ的距离的最大值．
21．（12分）函数f（x）＝x3+（1+a）x2+ax+c（a∈R）．
（1）求证：f（x）有且仅有两个极值点；
（2）设f（x）的两个极值点分别为x1，x2，且满足|x2﹣x1|＝，若函数f（x）有三个零点，求实数c的取值范围．
（二）选考题：共10分。请考生在第22、23题中任选一题作答。如果多做，则按所做的第一题记分。[选修：坐标系与参数方程]
22．（10分）已知在平面直角坐标系xOy中，直线l的参数方程为（t为参数），以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ2+2ρsinθ﹣3＝0，点P的极坐标是（4，）．
（1）求直线l的极坐标方程及点P到直线l的距离；
（2）若直线l与曲线C交于A，B两点，求△PAB的面积．
[选修4-5：不等式选讲]（10分）
23．已知f（x）＝|x+a|•x+|x﹣2|•（x+a）（a∈R）．
（1）当a＝1时，求不等式f（x）≥0的解集；
（2）当x∈（﹣∞，﹣1）时，恒有f（x）＜0，求实数a的取值范围．

2021年云南省红河州高考数学第三次复习统一检测试卷（文科）
参考答案与试题解析
一、选择题：本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的.
1．（5分）已知集合A＝{x|x2﹣2x﹣3＜0，x∈N*}，B＝{﹣1，0，1，2}，则A∩B＝（　　）
A．{﹣1，0，1，2} B．{0，1，2} C．{1，2} D．{1，2，3}
【分析】先利用一元二次不等式的解法求出集合A，再由集合交集的定义求解即可．
【解答】解：因为集合A＝{x|x2﹣2x﹣3＜0，x∈N*}＝{x|﹣1＜x＜3，x∈N*}＝{1，2}，
又B＝{﹣1，0，1，2}，
则A∩B＝{1，2}．
故选：C．
2．（5分）已知复数，i为虚数单位，是z的共轭复数，则＝（　　）
A． B． C． D．
【分析】根据已知条件，结合共轭复数的概念，以及复数代数形式的乘法运算，即可求解．
【解答】解：∵＝，
∴．
故选：B．
3．（5分）已知，则＝（　　）
A． B．﹣ C． D．﹣
【分析】把看成一个整体，表示；再结合诱导公式，二倍角公式求解．
【解答】解：因为，
所以＝．
故选：A．
4．（5分）随着我国人民生活水平日益提高，餐饮消费在国民经济活动中的比重逐步加大．某机构统计了2014年至2020年（1月至11月）我国餐饮业销售收入的情况，得到下面的条形图，则下面说法中不正确的是（　　）

A．2014年至2019年，我国餐饮业销售收入逐年增加
B．2019年我国餐饮业销售收入较2018年的增量超过4000亿元，同比增长接近10%
C．2020年受新冠肺炎疫情影响，我国餐饮业销售收入有所下滑
D．近年来，我国餐饮业销售收入同比增长率有上升趋势
【分析】根据条形图的数据，依次判断，即可求解．
【解答】解：对于A选项，从条形图可得，2014年至2019年，我国餐饮业销售收入逐年增加，故A选项正确，
对于B选项，2018年和2019年我国餐饮业销售收入分别为42715.9亿元和46720.7亿元，
2019年较2018年增量为46720.7﹣42715.9＝4004.8亿元，
从折线图可以看成，同比增长接近10%（实际增长为9.38%），故B选项正确，
对于C选项，从条形图可得，2020年我国餐饮业销售收入有所下滑，故C选项正确，
对于D选项，从折线图可得，我国餐饮业销售收入同比增长率有上升趋势，故D选项错误．
故选：D．
5．（5分）下列说法中，正确的个数为（　　）
①若，是非零向量，则“＞0”是“与的夹角为锐角”的充要条件；
②命题“在△ABC中，若sinA＞sinB，则A＞B”的逆否命题为真命题；
③已知命题p：，则它的否定是￢p：∀x∉R，x2+x+2＞0．
A．0 B．1 C．2 D．3
【分析】①利用平面向量的数量积和夹角的应用判断，②利用正弦定理，以及大边对大角判断，③用含有特称量词的命题的否定判断，即可求解．
【解答】解：对于①，∵，是非零向量，当两向量同向时，依然可以得到，故①错误，
对于②，在△ABC中，由sinA＞sinB，可得a＞b，即A＞B，逆否命题与原命题真假性相同，故②正确，
对于③，命题p：，则它的否定是￢p：∀x∈R，x2+x+2＞0，故③错误．
故选：B．
6．（5分）在三棱锥P﹣ABC中，已知PA，PB，PC两两垂直，且PA＝1，PB＝2，PC＝3，则三棱锥P﹣ABC的外接球的表面积为（　　）
A．13π B．14π C．56π D．64π
【分析】由题意把三棱锥P﹣ABC放置在一个长方体中，求出长方体的外接球的表面积，即为三棱锥P﹣ABC的外接球的表面积．
【解答】解：把三棱锥P﹣ABC放置在一个长方体中，如图：

则长方体的外接球即三棱锥的外接球，
其外接球的半径为R＝．
∴三棱锥P﹣ABC的外接球的表面积为4π×．
故选：B．
7．（5分）函数f（x）＝•cosx的图象大致是（　　）
A． B．
C． D．
【分析】判断函数的奇偶性，排除选项，利用特殊点的位置判断即可．
【解答】解：函数f（x）＝•cosx，可知：f（﹣x）＝•cosx＝﹣•cosx＝﹣f（x），函数是奇函数．
排除A、B，当x∈（0，）时，f（x）＞0，排除D，
故选：C．
8．（5分）如图所示，网格中小正方形的边长均为1，△ABC的三个顶点均在小正方形的顶点处，则△ABC外接圆的面积为（　　）

A． B． C． D．
【分析】直接利用正弦定理余弦定理及圆的面积公式的应用求出结果．
【解答】解：如图所示：|AB|＝，，|BC|＝3；
利用余弦定理：cosC＝，
所以sinC＝，
故2R＝，解得R＝，
所以．
故选：C．
9．（5分）已知55＞3，a＝log23，b＝log35，c＝，则（　　）
A．a＞b＞c B．c＞a＞b C．a＞c＞b D．b＞c＞a
【分析】根据即可得出a＞c，再根据即可得出a，b，c的大小关系．
【解答】解：∵55＞3，
∴，，
又，，
∴a＞b＞c．
故选：A．
10．（5分）已知实数x，y满足约束条件|x±y|≤2，若在该区域内随机取一点P（x，y），则该点落在所表示的曲线与x轴围成的图形内部的概率为（　　）
A． B． C． D．
【分析】根据题意，分析不等式组|x±y|≤2对应的平面区域以及曲线与x轴围成的图形的面积，由几何概型公式计算可得答案．
【解答】解：根据题意，|x±y|≤2，即，其对应的平面区域为正方形ABCD，
其面积S＝（2）×（2）＝8，
，变形可得x2+y2＝1，（y≥0），该曲线与x轴围成的图形为半圆，
其面积S1＝×π×12＝，
故该点落在所表示的曲线与x轴围成的图形内部的概率P＝＝；
故选：D．

11．（5分）已知数列{an}的前n项和为Sn，且满足Sn＝4n2+n（n∈N*）．若数列{bn}满足bn＝，则++…+＝（　　）
A． B． C． D．
【分析】由已知递推式可得Sn﹣1＝4（n﹣1）2+n﹣1，利用作差法求得an，再验证首项，代入bn＝，然后利用裂项相消法求和．
【解答】解：由Sn＝4n2+n，得Sn﹣1＝4（n﹣1）2+n﹣1（n≥2），
可得an＝Sn﹣Sn﹣1＝8n﹣3（n≥2），
当n＝1时，a1＝S1＝5适合上式，则an＝8n﹣3．
∴bn＝＝，
故，
∴++…+＝＝．
故选：D．
12．（5分）已知函数f（x）是R的奇函数，且满足f（x+1）＝f（x﹣1），当x∈（0，1]，f（x）＝lnx，则下列关于函数f（x）叙述正确的是（　　）
A．函数f（x）的最小正周期为1
B．函数f（x）在（0，2021）内单调递增
C．函数f（x）相邻两个对称中心的距离为2
D．函数y＝f（x）+lnx在区间（0，2021）内有1011个零点
【分析】利用奇函数f（x）满足f（x+1）＝f（x﹣1），对该函数的周期性、对称性及单调性进行分析，即可判断正误．
【解答】解：因为奇函数f（x）满足f（x+1）＝f（x﹣l），所以f（1+x）＝﹣f（1﹣x）
所以f（x+2）＝f[（x+1）+1]＝f[（x+1）﹣1]＝f（x），故周期为2；
由奇函数f（x）满足f（x+1）＝f（x﹣l），还可得f（1+x）＝﹣f（1﹣x），即函数的图象关于点（1，0）对称，可得f（x）的大致图象如下：

故A、B错
可得函数f（x）的图象关于点（k，0）（k∈Z）对称，故相邻两个对称中心的距离为1，故C错误；y＝f（x）的图象与y＝﹣lnx的图象在每个（2k，2k+2）区间内都有1个交点，所以在（0，2021）内有1011个交点，故函数y＝f（x）+lnx在区间（0，2021）内有1011个零点，故D正确；
故选：D．
二、填空题：本题共4小题，每小题5分，共20分.
13．（5分）若△ABC是边长为1的等边三角形，则＝　　．
【分析】直接利用向量的数量积公式化简求解即可．
【解答】解：△ABC是边长为1的等边三角形，则＝＝．
故答案为：﹣．
14．（5分）函数在（﹣π，π）上的零点之和为　﹣　．
【分析】令＝0，得sin（2x﹣）＝，依题意知2x﹣∈（﹣，），从而可求得x＝，或﹣，或，或﹣，求和可得答案．
【解答】解：令＝0，得sin（2x﹣）＝，
x∈（﹣π，π）⇒2x﹣∈（﹣，），
则2x﹣＝，或﹣2π，或，或﹣2π，
解得x＝，或﹣，或，或﹣，
所以函数在（﹣π，π）上的零点之和为+（﹣）++（﹣）＝﹣，
故答案为：﹣．
15．（5分）已知双曲线，过下焦点F作斜率为2的直线与双曲线的一条渐近线相交于点A，且A在第一象限，若|OA|＝|OF|（O为坐标原点），则双曲线C的离心率为　　．
【分析】设直线AF的方程与双曲线的渐近线方程联立，求出点A的坐标，再由|OA|＝|OF|＝c，列式化简，可得a与c的关系，即可得到答案．
【解答】解：设直线AF的方程为y＝2x﹣c，双曲线C的渐近线方程为，
联立方程组，解得，
则，
因为|OA|＝|OF|＝c，
则，
化简可得a2+b2＝（2b﹣a）2，
整理可得4a＝3b，
所以16a2＝9c2﹣9a2，即25a2＝9c2，
所以，
则e＝．
故答案为：．
16．（5分）丹麦数学家琴生是19世纪对数学分析做出卓越贡献的巨人，特别是在函数的凹凸性与不等式方面留下了很多宝贵的成果．定义：函数f（x）在（a，b）上的导函数为f'（x），f'（x）在（a，b）上的导函数为f''（x），若在（a，b）上f''（x）＜0恒成立，则称函数f（x）是（a，b）上的“严格凸函数”，称区间（a，b）为函数f（x）的“严格凸区间”．则下列正确命题的序号为 　①②　．
①函数f（x）＝﹣x3+3x2+2在（1，+∞）上为“严格凸函数”；
②函数的“严格凸区间”为；
③函数在（1，4）为“严格凸函数”，则m的取值范围为[e﹣1，+∞）．
【分析】根据所给定义逐一进行判断即可．
【解答】解：对①：f'（x）＝﹣3x²+6x，f''（x）＝﹣6x+6，f''（x）＜0在（1，+∞）上恒成立，所以函数f（x）在（1，+∞）上为“严格凸函数”，故①正确；
对②：f'（x）＝，f''（x）＝，f''（x）＜0即2lnx﹣3＜0，解得x∈（0，），所以函数f（x）的“严格凸区间”为（0，），故②正确；
对③：f'（x）＝ex﹣lnx﹣1﹣mx，f''（x）＝ex﹣﹣m，f''（x）＜0，即ex﹣﹣m＜0在（1，4）上恒成立，即m＞ex﹣，设g（x）＝ex﹣，则g（x）在（1，4）上单调递增，
所以g（x）＜，即m≥，所以③错误；
故答案为：①②．
三、解答题：共70分。解答应写出文字说明、证明过程或演算步骤。第题为必考题，每个试题考生都必须作答.第、题为选考题，考生根据要求作答.（一）必考题：共分.
17．（12分）已知公差不为0的等差数列{an}的前n项和为Sn，且S3＝9，a1，a2，a5成等比数列．
（1）求数列{an}的通项公式；
（2）若数列{bn}满足，求数列{bn﹣an}的前n项和Tn．
【分析】（1）设公差为d，d不为0，由等比数列的中项性质和等差数列的通项公式、求和公式，解方程可得首项和公差，进而得到an；
（2）求得bn﹣an＝4n﹣（2n﹣1），由数列的分组求和，结合等差数列和等比数列的求和公式，计算可得所求和．
【解答】解：（1）设公差为d，d不为0，
由S3＝9，可得3a1+3d＝9，即a1+d＝3，
由a1，a2，a5成等比数列，可得a22＝a1a5，
即（a1+d）2＝a1（a1+4d），即有d＝2a1，
可得a1＝1，d＝2，
所以an＝1+2（n﹣1）＝2n﹣1；
（2）＝4n，
bn﹣an＝4n﹣（2n﹣1），
前n项和Tn＝（4+16+...+4n）﹣（1+3+5+...+2n﹣1）
＝﹣n（1+2n﹣1）
＝﹣n2．
18．（12分）某市从2020年5月1日开始，若电子警察抓拍到机动车不礼让行人的情况后，交警部门将会对不礼让行人的驾驶员进行扣3分，罚款200元的处罚，并在媒体上曝光．但作为交通重要参与者的行人，闯红灯通行却频有发生，带来了较大的交通安全隐患和机动车通畅率降低点情况．交警部门在某十字路口根据以往的监测数据，得到行人闯红灯的概率为0.2，并从穿越该路口的行人中随机抽取了200人进行调查，对是否存在闯红灯的情况进行统计，得到2×2列联表如下：

45岁以下
45岁以上
合计
闯红灯人数

25

未闯红灯人数
85


合计


200
近期，为了整顿“行人闯红灯”这一不文明的违法行为，交警部门在该十字路口试行了对闯红灯的行人进行5元以上，50元以下的经济处罚．在试行经济处罚一段时间后，交警部门再次对穿越该路口的行人中随机抽取了200人进行调查，对是否存在闯红灯的情况进行统计，得到2×2列联表如下：

45岁以下
45岁以上
合计
闯红灯人数
5
15
20
未闯红灯人数
95
85
180
合计
100
100
200
将统计数据所得频率视为概率，完成下列问题：
（1）将2×2列联表填写完整（不需要写出填写过程），并根据表中数据分析，在试行对闯红灯的行人进行经济处罚前，是否有90%的把握认为闯红灯行为与年龄有关；
（2）在试行对闯红灯的行人进行经济处罚后，闯红灯现象是否有明显改善，请说明理由；
（3）结合调查结果，请你对“如何治理行人闯红灯现象”提出合理的建议（至少提出两条建议）．
参考公式：，其中n＝a+b+c+d．
参考数据：
P（K2≥k0）
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k0
1.132
2.072
2.706
3.841
5.024
6.635
7.879
10.828
【分析】（1）根据已知条件，结合独立性检验公式，即可求解．
（2）对比试行对闯红灯的行人进行经济处罚前后，行人闯红灯的概率，即可得出结论．
（3）结合（1），（2）的结论，可分别提出针对45岁以上人群开展“道路安全”宣传教育，以及在法律允许范围内进行适当的经济处罚．
【解答】解：（1）∵行人闯红灯的概率为0.2，
∴行人闯红灯的人数为0.2×200＝40，
2×2列联表如下：

45岁以下
45岁以上
合计
闯红灯人数
15
25
40
未闯红灯人数
85
75
160
合计
100
100
200
∵，
∴有90%的把握认为闯红灯行为与年龄有关．
（2）在试行对闯红灯的行人进行经济处罚后，行人闯红灯的概率为，
而在试行对闯红灯的行人进行经济处罚前，行人闯红灯的概率为0.2，
故在试行对闯红灯的行人进行经济处罚后，闯红灯现象有明显改善．
（3）①根据调查数据显示，行人闯红灯与年龄有明显关系，故可以针对45岁以上人群开展“道路安全”宣传教育．
②由于在试行对闯红灯的行人进行经济处罚，可以明显降低行人闯红灯的概率，故可以在法律允许范围内进行适当的经济处罚．
19．（12分）如图，在四棱锥P﹣ABCD中，四边形ABCD为直角梯形，AB∥CD，AB⊥BC，AB＝BC＝2CD＝4，PA＝2，PB＝2，E为BC的中点，且PE⊥BD．
（1）证明：PA⊥平面ABCD；
（2）线段PB上是否存在一点M，使得三棱锥A﹣DEM的体积为？若存在，试确定点M的位置；若不存在，请说明理由．

【分析】（1）连接AE，且AE与BD的交点为O，利用三角形全等以及平面几何知识，证明BD⊥AE，结合BD⊥PE，即可证明BD⊥平面PAE，从而得到BD⊥PA，再利用勾股定理可得PA⊥AB，由线面垂直的判定定理证明PA⊥平面ABCD即可；
（2）过点M作MH⊥AB于点H，取AB的中点为G，连接DG，利用边角关系求解所需线段的长度，求出△ADE的面积，证明MH⊥平面ADE，则线段MH的长即为三棱锥M﹣ADE的高，利用等体积法VA﹣DEM＝VM﹣ADE，求解MH，即可得到答案．
【解答】（1）证明：如图，连接AE，且AE与BD的交点为F，
因为AB＝BC，BE＝BC＝1＝CD，∠ABE＝∠BCD＝90°，
所以△ABE≌△BCD，
故∠BAE＝∠CBD，
因为∠ABD+∠CBD＝90°，
则∠ABD+∠BAE＝90°，
故∠AFB＝90°，即BD⊥AE，
又BD⊥PE，且PE∩AE＝E，PE，AE⊂平面PAE，
所以BD⊥平面PAE，
因为PA⊂平面PAE，则BD⊥PA，
在△PAB中，PA2+AB2＝PB2，则PA⊥AB，
又BD∩AB＝BA，BD，AB⊂平面ABCD，
故PA⊥平面ABCD；
（2）解：线段PB上存在一点M，点M为靠近点B的三等分点，使得三棱锥A﹣DEM的体积为．
证明如下：
如图，过点M作MH⊥AB于点H，取AB的中点为G，连接DG，
因为直角梯形ABCD中，有AB∥CD，AB⊥BC，且AB＝BC＝4，CD＝2，
所以DG⊥AB且DG＝BC＝4，AG＝2，
则AD＝，
因为DE＝且AE＝，
故＝，
由（1）可知，PA⊥平面ABCD，AB⊂平面ABCD，
所以PA⊥AB，
因为MH⊥AB，且MH，PA，AB⊂平面PAB，
所以MH∥PA，
则MH⊥平面ABCD，即MH⊥平面ADE，
所以线段MH的长即为三棱锥M﹣ADE的高，
由等体积法VA﹣DEM＝VM﹣ADE＝，
解得，
所以，
故线段PB上存在一点M，点M为靠近点B的三等分点，使得三棱锥A﹣DEM的体积为．


20．（12分）已知抛物线C：y2＝2px（p＞0）的准线经过椭圆的一个焦点．
（1）求抛物线C的方程；
（2）过椭圆的右顶点且斜率为k1，k2的两条直线分别交抛物线C于点A，B，M，N，点P，Q分别是线段AB，MN的中点，若k1+k2＝2，求抛物线C的焦点F到直线PQ的距离的最大值．
【分析】（1）先求出椭圆的焦点坐标，由抛物线的准线经过焦点求解即可；
（2）设直线AB的方程，与抛物线联立，利用韦达定理求出点P的坐标，同理求出点Q的坐标，从而求出直线PQ的方程，即可得到答案．
【解答】解：（1）因为椭圆的焦点坐标为，
抛物线C的准线方程为，
所以，解得p＝1，
故抛物线C的方程为y2＝2x；
（2）设直线AB的方程为y＝k1（x﹣1），设A（x1，y1），B（x2，y2），
联立，可得，
则，
且，，
故，
同理可得，
则直线PQ的方程为，
即＝＝，
故直线PQ经过定点D（1，），
所以焦点F到直线PQ的距离的最大值为|DF|＝．
21．（12分）函数f（x）＝x3+（1+a）x2+ax+c（a∈R）．
（1）求证：f（x）有且仅有两个极值点；
（2）设f（x）的两个极值点分别为x1，x2，且满足|x2﹣x1|＝，若函数f（x）有三个零点，求实数c的取值范围．
【分析】（1）证明方程f′（x）＝0有两个变号的根即可．
（2）利用韦达定理可得条件|x2﹣x1|＝，求出a＝0或a＝1，再进行分类讨论，根据三次函数的图象特征得到不等式组，进而求得c的取值范围．
【解答】解：（1）证明：由题意可得f′（x）＝3x2+2（1+a）x+a，
令f′（x）＝0，得方程3x2+2（1+a）+a＝0，
△＝4（1+a）2﹣12a＝4（a2﹣a+1）＞0，恒成立，
所以f′（x）＝0有两个根，
不妨设为x1，x2，且x1＜x2，
所以当x∈（﹣∞，x1），f′（x）＞0，f（x）单调递增，
当x∈（x1，x2），f′（x）＜0，f（x）单调递减，
当x∈（x2，+∞），f′（x）＞0，f（x）单调递增，
所以f（x）有两个极值点．
（2）由（1）得f（x）的极值点分别为x1，x2，
则x1，x2是方程3x2+2（1+a）+a＝0的两个根，
所以x1+x2＝﹣（1+a），x1x2＝，
因为|x2﹣x1|＝，
所以|x2﹣x1|2＝（x2+x1）2﹣4x1x2＝（a+a）2﹣＝，
解得a＝0或a＝1，
①当a＝0时，f（x）＝x3+x2+c，
f′（x）＝3x2+2x＝x（3x+2），
令f′（x）＝0，得x1＝﹣，x2＝0，
所以f（x）在（﹣∞，﹣）单调递增，在（﹣，0）上单调递减，在（0，+∞）上单调递增，
所以f（x）的极大值为f（﹣），极小值为f（0），
要使得函数f（x）有三个零点，只需，解得c∈（﹣，0）．
②当a＝1时，f（x）＝x3+2x2+x+c，
f′（x）＝3x2+4x+1＝（x+1）（3x+1），
令f′（x）＝0，得x1＝﹣1，x2＝﹣，
所以f（x）在（﹣∞，﹣1）上单调递增，在（﹣1，﹣）上单调递减，在（﹣，+∞）上单调递增，
所以f（x）的极大值为f（﹣1），极小值为f（﹣），
要使得函数f（x）有三个零点，只需，解得c∈（0，），
综上所述，当a＝0时，c∈（﹣，0），
当a＝1时，c∈（0，）．
（二）选考题：共10分。请考生在第22、23题中任选一题作答。如果多做，则按所做的第一题记分。[选修：坐标系与参数方程]
22．（10分）已知在平面直角坐标系xOy中，直线l的参数方程为（t为参数），以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ2+2ρsinθ﹣3＝0，点P的极坐标是（4，）．
（1）求直线l的极坐标方程及点P到直线l的距离；
（2）若直线l与曲线C交于A，B两点，求△PAB的面积．
【分析】（1）由，消去t得到y＝，再利用x＝ρcosθ，y＝ρsinθ，求得极坐标方程，然后利用直线的极坐标方程求点（4，）到直线l的距离即可；
（2）将曲线C的极坐标方程和直线的极坐标方程联立，得到，求出|AB|，再求出△PAB的面积．
【解答】解：（1）由，消去t得到y＝，
则，所以tan，
所以直线l的极坐标方程为，
所以点（4，）到直线l的距离为d＝4sin（）＝2．
（2）由，得，
设A（），B（），则，ρ1ρ2＝﹣3，
所以|AB|＝|ρ1﹣ρ2|＝，
所以△PAB的面积S＝．
[选修4-5：不等式选讲]（10分）
23．已知f（x）＝|x+a|•x+|x﹣2|•（x+a）（a∈R）．
（1）当a＝1时，求不等式f（x）≥0的解集；
（2）当x∈（﹣∞，﹣1）时，恒有f（x）＜0，求实数a的取值范围．
【分析】（1）把a＝1代入f（x），利用零点分段法去掉绝对值，分段求出不等式的解集，再求并集即可；
（2）x∈（﹣∞，﹣1）时，x﹣2＜0，分情况讨论a≤1和a＞1时|x+a|的正负，去掉绝对值，代入f（x）判断f（x）＜0是否恒成立，从而求出a的取值范围．
【解答】解：（1）a＝1时，f（x）＝|x+1|•x+|x﹣2|•（x+1）＝；
不等式f（x）≥0等价于，或，或；
解得x≥2或﹣1≤x＜2或∅，
所以不等式f（x）≥0的解集为{x|x≥﹣1}；
（2）当x∈（﹣∞，﹣1）时，x﹣2＜0，
f（x）＝|x+a|•x+（2﹣x）•（x+a）＝|x+a|•x+（2﹣a）x﹣x2+2a，且f（﹣a）＝0；
当a≤1时，x+a＜0，f（x）＝﹣（x+a）•x+（2﹣a）x﹣x2+2a＝﹣2x2+（2﹣2a）x+2a＝2（﹣x+1）（x+a），
由f（x）＜0，得出2（﹣x+1）（x+a）＜0，
因为﹣x+1＞0，且x+a＜0，所以f（x）＜0恒成立；
当a＞1时，f（x）＝，
若﹣a≤x＜﹣1，且x+a＞0时，则f（x）＜0不恒成立，不满足题意；
综上知，f（x）＜0恒成立时实数a的取值范围是a≤1．