专题02 全等三角形模型解题-决胜中考数学之模型解题高分攻略（学生版）

专题二 全等三角形模型解题

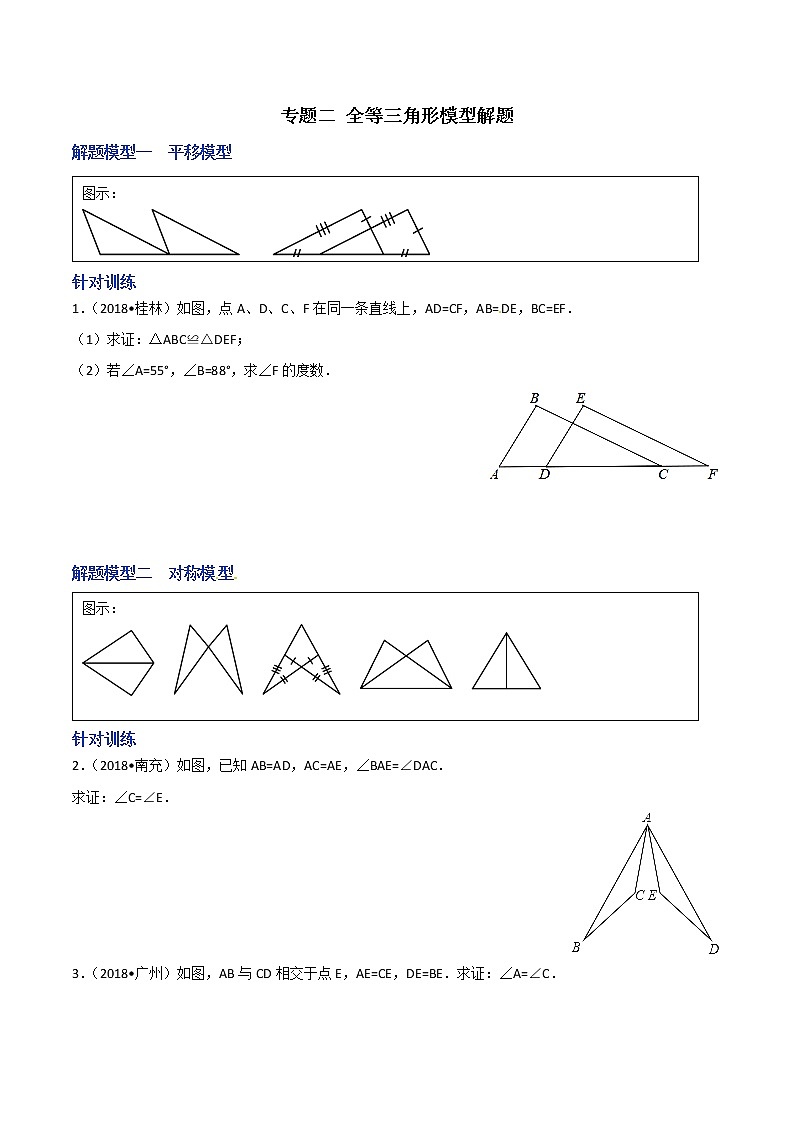
解题模型一  平移模型

针对训练

1．（2018•桂林）如图，点A、D、C、F在同一条直线上，AD=CF，AB=DE，BC=EF．

（1）求证：△ABC≌△DEF；

（2）若∠A=55°，∠B=88°，求∠F的度数．

[来源:ZXXK]

解题模型二  对称模型

针对训练

2．（2018•南充）如图，已知AB=AD，AC=AE，∠BAE=∠DAC．

求证：∠C=∠E．

3．（2018•广州）如图，AB与CD相交于点E，AE=CE，DE=BE．求证：∠A=∠C．

　4．（2018•乐山）如图，已知∠1=∠2，∠3=∠4，求证：BC=BD．

[来源:Z.xx.k.Com]

5．（2017•郴州）已知△ABC中，∠ABC=∠ACB，点D，E分别为边AB、AC的中点，求证：BE=CD．[来源:Z_xx_k.Com]

6．（2018•武汉）如图，点E、F在BC上，BE=CF，AB=DC，∠B=∠C，AF与DE交于点G，求证：GE=GF．

7．（2018•泰州）如图，∠A=∠D=90°，AC=DB，AC、DB相交于点O．求证：OB=OC．

8．（2018•镇江）如图，△ABC中，AB=AC，点E，F在边BC上，BE=CF，点D在AF的延长线上，AD=AC．

（1）求证：△ABE≌△ACF；[来源:Z§xx§k.Com]

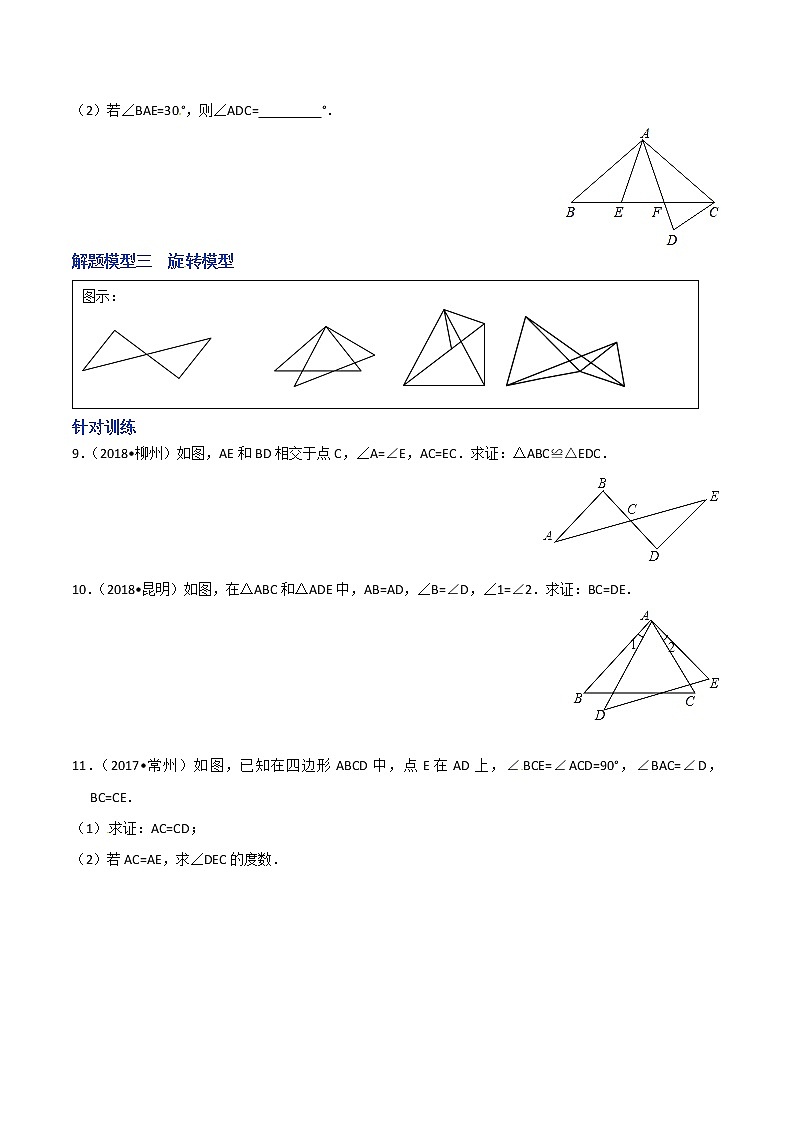
（2）若∠BAE=30°，则∠ADC=　     　°．

解题模型三  旋转模型

针对训练

9．（2018•柳州）如图，AE和BD相交于点C，∠A=∠E，AC=EC．求证：△ABC≌△EDC．

10．（2018•昆明）如图，在△ABC和△ADE中，AB=AD，∠B=∠D，∠1=∠2．求证：BC=DE．

11．（2017•常州）如图，已知在四边形ABCD中，点E在AD上，∠BCE=∠ACD=90°，∠BAC=∠D，BC=CE．

（1）求证：AC=CD；

（2）若AC=AE，求∠DEC的度数．

12．（2017•恩施州）如图，△ABC、△CDE均为等边三角形，连接BD、AE交于点O，BC与AE交于点P．求证：∠AOB=60°．

解题模型四  平移+旋转模型

针对训练

13．（2018•菏泽）如图，AB∥CD，AB=CD，CE=BF．请写出DF与AE的数量关系，并证明你的结论．

14．（2017•孝感）如图，已知AB=CD，AE⊥BD，CF⊥BD，垂足分别为E，F，BF=DE，求证：AB∥CD．

15．（2018•铜仁）已知：如图，点A、D、C、B在同一条直线上，AD=BC，AE=BF，CE=DF，求证：AE∥FB．

16．（2018•怀化）已知：如图，点A，F，E，C在同一直线上，AB∥DC，AB=CD，∠B=∠D．

（1）求证：△ABE≌△CDF；

（2）若点E，G分别为线段FC，FD的中点，连接EG，且EG=5，求AB的长．[来源:Z*X*X*K]

解题模型五  角平分线模型

针对训练

17.（2016•咸宁）证明命题“角的平分线上的点到角的两边的距离相等”，要根据题意，画出图形，并用符号表示已知和求证，写出证明过程，下面是小明同学根据题意画出的图形，并写出了不完整的已知和求证．

已知：如图，∠AOC=∠BOC，点P在OC上，　            　.

求证：　         　．

请你补全已知和求证，并写出证明过程．

解题模型六  三垂直模型

针对训练

18.在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E，求证：DE=AD+BE．

19.如图，将等腰直角三角形ABC的直角顶点置于直线l上，且过A，B两点分别作直线l的垂线，垂足分别为D，E，请你在图中找出一对全等三角形，并写出证明它们全等的过程．