2019_2020学年深圳市福田区八上期末数学试卷

这是一份2019_2020学年深圳市福田区八上期末数学试卷，共8页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共12小题；共60分）
1. 下列数据中不能作为直角三角形
A. 1，1，2B. 5，12，13C. 3，5，7D. 6，8，10

2. 4 的平方根是
A. 4B. −4C. 2D. ±2

3. 在给出一组数 0，π，5，3.1415926，39，227，0.1234567891011⋯（自然数依次相连），其中无理数有
A. 2 个B. 3 个C. 4 个D. 5 个

4. 下列计算正确的是
A. −16=−4B. 16=±4
C. −42=−4D. 3−43=−4

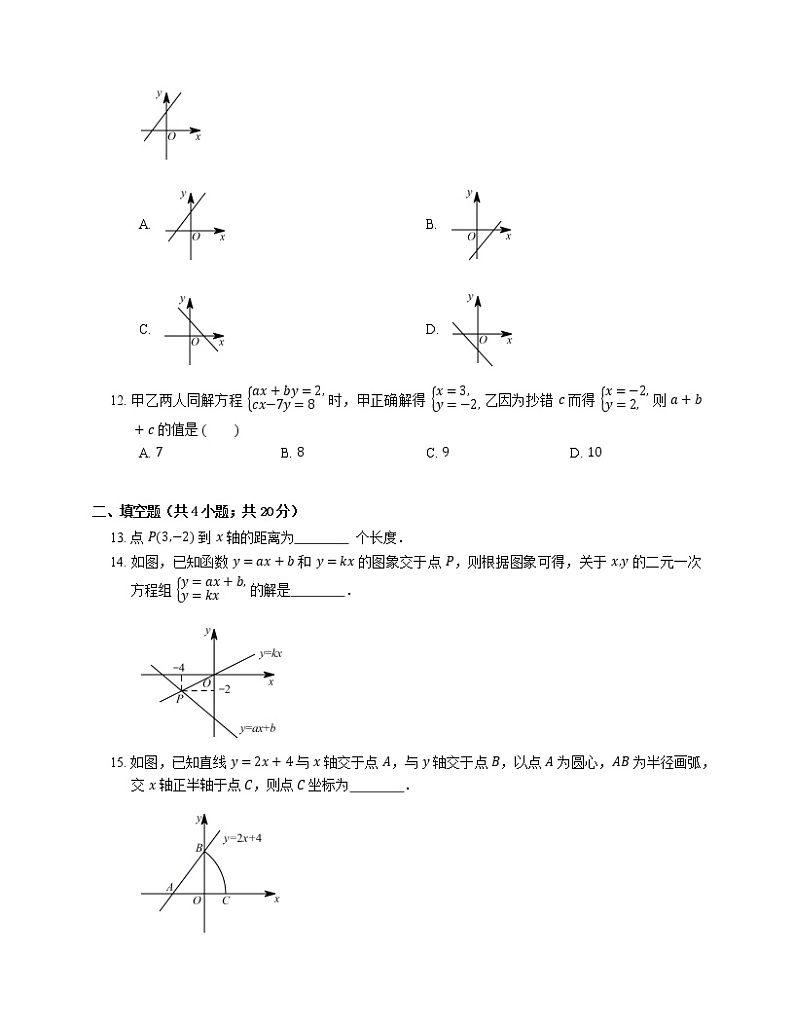
5. 在平面直角坐标系中，点 P1,−2 关于 y 轴的对称点的坐标是
A. −1,2B. −1,−2C. 1,2D. 2,−1

6. 下列命题是真命题的是
A. 同旁内角互补
B. 直角三角形的两个锐角互余
C. 三角形的一个外角等于它的两个内角之和
D. 三角形的一个外角大于任意一个内角

7. 如图，下列条件不能判断直线 a∥b 的是
A. ∠1=∠4B. ∠3=∠5C. ∠2+∠5=180∘D. ∠2+∠4=180∘

8. 某一次函数的图象经过点 1,2，且 y 随 x 的增大而减小，则这个函数的表达式可能是
A. y=2x+4B. y=3x−1C. y=−3x+1D. y=−2x+4

9. 已知小华上学期语文、数学、英语三科平均分为 92 分，他记得语文得了 88 分，英语得了 95 分，但他把数学成绩忘记了，你能告诉他应该是以下哪个分数吗?
A. 93B. 95C. 94D. 96

10. 已知点 −6,y1，3,y2，都在直线 y=−13x+5 上，则 y1 与 y2 的大小关系是
A. y1>y2B. y1=y2C. y1
11. 已知函数 y=kx+b 的图象如图所示，则函数 y=−bx+k 的图象大致是
A. B.
C. D.

12. 甲乙两人同解方程 ax+by=2,cx−7y=8 时，甲正确解得 x=3,y=−2, 乙因为抄错 c 而得 x=−2,y=2, 则 a+b+c 的值是
A. 7B. 8C. 9D. 10

二、填空题（共4小题；共20分）
13. 点 P3,−2 到 x 轴的距离为 个长度．

14. 如图，已知函数 y=ax+b 和 y=kx 的图象交于点 P，则根据图象可得，关于 x,y 的二元一次方程组 y=ax+b,y=kx 的解是 ．

15. 如图，已知直线 y=2x+4 与 x 轴交于点 A，与 y 轴交于点 B，以点 A 为圆心，AB 为半径画弧，交 x 轴正半轴于点 C，则点 C 坐标为 ．

16. 如图，已知一次函数 y=−x+1 的图象与 x 轴、 y 轴分别交于 A 点，B 点，点 M 在坐标轴上，并且使以点 A，B，M 为顶点的三角形是等腰三角形，则这样的点 M 有 个．

三、解答题（共7小题；共91分）
17. 计算：
（1）∣−3∣+327−10−16+13−1；
（2）2−52+5+2−22−12．

18. 解方程组：4x−3y=11,2x+y=13.

19. 如图所示，点 B，E 分别在 AC，DF 上，BD，CE 均与 AF 相交，∠1=∠2，∠C=∠D，求证：∠A=∠F．

20. 宣传交通安全知识，争做安全小卫士．某校进行“交通安全知识”宣传培训后进行了一次测试．学生考分按标准划分为不合格、合格、良好、优秀四个等级，为了解全校的考试情况，对在校的学生随机抽样调查，得到图（1）的条形统计图，请结合统计图回答下列问题：
（1）该校抽样调查的学生人数为 名；抽样中考生分数的中位数所在等级是 ；
（2）抽样中不及格的人数是多少?占被调查人数的百分比是多少?
（3）若已知该校九年级有学生 500 名，图（2）是各年级人数占全校人数的扇形图（图中圆心角被等分），请你估计全校优良（良好与优秀）的人数约有多少人?

21. 受地震的影响，某超市鸡蛋供应紧张，需每天从外地调运鸡蛋 1200 斤．超市决定从甲、乙两大型养殖场调运鸡蛋，已知甲养殖场每天最多可调出 800 斤，乙养殖场每天最多可调出 900 斤，从两养殖场调运鸡蛋到超市的路程和运费如表：
到超市的路程千米运费元/斤⋅千米甲养殖场2000.012乙养殖场1400.015
（1）若某天调运鸡蛋的总运费为 2670 元，则从甲、乙两养殖场各调运了多少斤鸡蛋?
（2）设从甲养殖场调运鸡蛋 x 斤，总运费为 W 元，试写出 W 与 x 的函数关系式，怎样安排调运方案才能使每天的总运费最省?

22. 如图，已知 P 为等边 △ABC 内的一点，且 PA=5，PB=3，PC=4，将线段 BP 绕点 P 按逆时针方向旋转 60∘ 至 PQ 的位置．
（1）求证：△ABP≌△CBQ；
（2）求证：∠BPC=150∘．

23. 如图，在平面直角坐标系中，过点 B6,0 的直线 AB 与直线 OA 相交于点 A4,2，动点 M 在线段 OA 和射线 AC 上运动．
（1）求直线 AB 的解析式．
（2）求 △OAC 的面积．
（3）是否存在点 M，使 △OMC 的面积是 △OAC 的面积的 14?若存在求出此时点 M 的坐标；若不存在，说明理由．
答案
第一部分
1. C
2. D
3. C
4. D
5. B
6. B
7. D
8. D
9. A
10. A
11. C
12. A
第二部分
13. 2
14. x=−4y=−2
15. 25−2,0
16. 7
第三部分
17. （1） 原式=3+1−4+3=3.
（2） 原式=4−5+4−42+2−22=5−922.
18.
4x−3y=11, ⋯⋯①2x+y=13. ⋯⋯②②×2−①
得：
5y=15.y=3.
把 y=3 代入 ② 得：
x=5.∴
方程组的解为
x=5,y=3.
19. ∵∠2=∠3，∠1=∠2，
∴∠1=∠3，
∴BD∥CE，
∴∠C=∠ABD．
又 ∵∠C=∠D，
∴∠D=∠ABD，
∴AB∥EF，
∴∠A=∠F．
20. （1） 50；良好
【解析】8+14+18+10=50，中位数位于良好里面．
（2） 8 人，850×100%=16%．
抽样中不及格的人数是 8 人．占被调查人数的百分比是 16%．
（3）
500÷412=1500.
1500×2850=840人.
全校优良人数有 840 人．
21. （1） 设从甲养殖场调运鸡蛋 x 斤，从乙养殖场调运鸡蛋 y 斤，
根据题意得：
200×0.012x+140×0.015y=2670,x+y=1200.
解得：
x=500,y=700.∵500<800
，700<900，
∴ 符合条件．
答：从甲、乙两养殖场各调运了 500 斤，700 斤鸡蛋．
（2） 从甲养殖场调运了 x 斤鸡蛋，从乙养殖场调运了 1200−x 斤鸡蛋，
根据题意得：
x≤800,1200−x≤900.
解得：
300≤x≤800.
总运费
W=200×0.012x+140×0.015×1200−x=0.3x+2520300≤x≤800.
∵W 随 x 的增大而增大，
∴ 当 x=300 时，W最小=2610 元，
∴ 每天从甲养殖场调运 300 斤鸡蛋，从乙养殖场调运 900 斤鸡蛋，每天的总运费最省．
22. （1） ∵ BP=PQ，∠BPQ=60∘，
∴ △BPQ 为等边三角形，
又 ∵ △ABC 是等边三角形，
∴ AB=BC，∠ABC=60∘，
∴ ∠PBQ=∠ABC，
∴ ∠ABP=∠CBQ，
在 △ABP 和 △CBQ 中，
AB=CB,∠ABP=∠CBQ,BP=BQ,
∴ △ABP≌△CBQSAS．
（2） ∵ △ABP≌△CBQ，
∴ PA=QC=4，
∵ BP=PQ，∠BPQ=60∘，
∴ △PBQ 是等边三角形，
∴ PQ=3，∠BPQ=60∘，
∵ 在 △PQC 中，PC2+PQ2=43+32=52=QC2，
∴ △PQC 是直角三角形，
∴ ∠QPC=90∘，
∴ ∠BPC=∠BPQ+∠QPC=60∘+90∘=150∘．
23. （1） 设直线 AB 的解析式是 y=kx+b，
根据题意得：4k+b=2,6k+b=0,
解得：k=−1,b=6.
则直线的解析式是：y=−x+6；
（2） 在 y=−x+6 中，令 x=0，解得：y=6，
S△OAC=12×6×4=12；
（3） 设 OA 的解析式是 y=mx，则 4m=2，
解得：m=12．
则直线的解析式是：y=12x，
∵ 当 △OMC 的面积是 △OAC 的面积的 14 时，
∴ 当 M 的横坐标是 14×4=1，
在 y=12x 中，当 x=1 时，y=12，则 M 的坐标是 1,12．
在 y=−x+6 中，x=1 则 y=5，则 M 的坐标是 1,5．
则 M 的坐标是：M11,12 或 M21,5．
当 M 的横坐标是：−1，
在 y=−x+6 中，当 x=−1 时，y=7，则 M 的坐标是 −1,7；
综上所述：M 的坐标是：M11,12 或 M21,5 或 M3−1,7．