2019_2020学年重庆市南开（融侨）中学九上期末数学试卷

这是一份2019_2020学年重庆市南开（融侨）中学九上期末数学试卷，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共12小题；共60分）
1. 2017 的绝对值是
A. −2017B. 2017C. 12017D. −12017

2. 下列计算结果正确的是
A. 2+5=25B. 6÷2=3
C. −2a23=−6a6D. x+12=x2+1

3. 下列英文字母既是轴对称图形又是中心对称图形的是
A. B.
C. D.

4. 如图，工人师傅在工程施工中需在同一平面内弯制一个变形管道 ABCD，使其拐角 ∠ABC=150∘，∠BCD=30∘，则
A. AB∥BCB. BC∥CD
C. AB∥DCD. AB 与 CD 相交

5. 如图，数轴上点 A 表示的数可能是
A. 4 的算术平方根B. 4 的立方根
C. 8 的平方根D. 8 的算术平方根

6. 下列说法正确的是
A. 了解 2017 年报考飞行员的学生的视力情况应采取抽样调查
B. 打开电视机，正在播放“神奇的动物去哪里”制作花絮是必然事件
C. 为了解初三 1200 名学生的体能状况，从中抽取了 100 名学生的成绩进行分析，1200 是样本容量
D. 7，9，9，4，9，8，8，这组数据的众数是 9

7. 在函数 y=x+2x−1 中，自变量 x 的取值范围是
A. x>1B. x≥−2
C. x≥−2 且 x≠1D. x>1 且 x≠−2

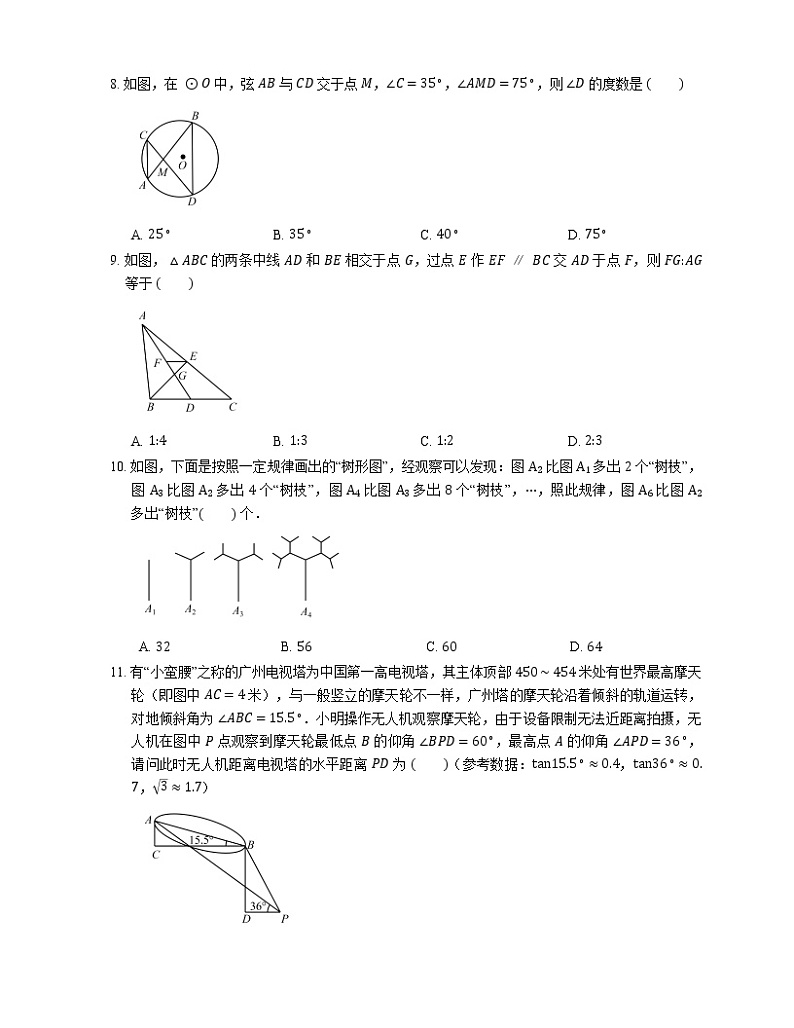
8. 如图，在 ⊙O 中，弦 AB 与 CD 交于点 M，∠C=35∘，∠AMD=75∘，则 ∠D 的度数是
A. 25∘B. 35∘C. 40∘D. 75∘

9. 如图，△ABC 的两条中线 AD 和 BE 相交于点 G，过点 E 作 EF∥BC 交 AD 于点 F，则 FG:AG 等于
A. 1:4B. 1:3C. 1:2D. 2:3

10. 如图，下面是按照一定规律画出的“树形图”，经观察可以发现：图 A2 比图 A1 多出 2 个“树枝”，图 A3 比图 A2 多出 4 个“树枝”，图 A4 比图 A3 多出 8 个“树枝”，⋯，照此规律，图 A6 比图 A2 多出“树枝” 个．
A. 32B. 56C. 60D. 64

11. 有“小蛮腰”之称的广州电视塔为中国第一高电视塔，其主体顶部 450∼454 米处有世界最高摩天轮（即图中 AC=4 米），与一般竖立的摩天轮不一样，广州塔的摩天轮沿着倾斜的轨道运转，对地倾斜角为 ∠ABC=15.5∘．小明操作无人机观察摩天轮，由于设备限制无法近距离拍摄，无人机在图中 P 点观察到摩天轮最低点 B 的仰角 ∠BPD=60∘，最高点 A 的仰角 ∠APD=36∘，请问此时无人机距离电视塔的水平距离 PD 为 （参考数据：tan15.5∘≈0.4，tan36∘≈0.7，3≈1.7）
A. 3B. 2.7C. 3.3D. 3.7

12. 若实数 a 使函数 y=a+6x2−3x+a+5a+6 的图象同时经过四个象限，并且使不等式组 x−12+x+a3<1,x−2≥3 无解，则所有符合条件的整数 a 的积是
A. −336B. 56C. 0D. 42

二、填空题（共6小题；共30分）
13. 11 月 30 日消息，近日工信部公布了截止 10 月末通信业的各项数据．数据显示，我国移动电话 4G 用户持续爆发式增长，总数达到 714000000 户，其中 714000000 用科学记数法表示为 ．

14. π−30+2−1−12−2= ．

15. 如图，边长为 3 的正方形 ABCD，以 A 为圆心，AB 为半径作弧交 DA 的延长线于 E，连接 CE，则图中阴影部分的面积为 ．

16. 现将背面完全相同，正面分别标有数 −2，−1，0，1 的 4 张卡片洗匀后，背面朝上，从中任取两张，将该卡片上的数字分别记为 m，n，则使点 Pm,n 在平面直角坐标系 xOy 内，落在直线 y=−x+1 上的概率为 ．

17. 小明和小强分别从A，B两地出发匀速相向而行，达到对方出发地后均立即以原速返回．已知小明到达B地半小时后，小强到达A地．如图表示他们出发时间 t（单位：小时）与距离A地的路程 S（单位：千米）之间的关系图，则出发后 小时，小明和小强第 2 次相遇．

18. 如图，在边长为 2 的菱形 ABCD 中，∠BAD=60∘，现有 ∠BFE=30∘ 的三角板 △BEF，BE，BF 所在直线分别交线段 AC 于点 M，N，若点 C 关于直线 BE 的对称点为 Cʹ，当 CʹN⊥AC 时，AN 的长为 ．

三、解答题（共8小题；共104分）
19. 已知：在平行四边形 ABCD 中，O 是对角线 BD 的中点，P 为线段 BC 上一点，连接 PO 并延长交 AD 于点 Q，求证：OP=OQ．

20. 所谓气质，是指婴儿出生后最早表示出来的一种较为明显而稳定的人格特征类型，也指孩子对身体内在或外来刺激反应的方式．心理学界常将气质分为四大类：胆汁型、多血质、黏液质、抑郁质．我校心理协会为了更好的了解学生，在高中随机发放了若干份问卷调查，并将统计结果绘制成统计图和统计表：根据以上信息完成下列问题并补全频数分布直方图：
四种气质类型人数频数分布表
气质类型频数频率胆汁型180a多血质1400.28黏液质800.16抑郁质b0.20

（1）a= ，b= ；
（2）请你估计一下，高三年级 1200 名学生中，胆汁型和多血质的共有多少名?

21. 化简：
（1）x+2y2−x+2yx−2y；
（2）xx2−9÷23+x+13−x−1．

22. 如图，已知一次函数 y1=k1x+6 与反比例函数 y2=k2x 相交于 A，B，与 x 轴交于点 C，与 y 轴交于点 E，过点 B 作 BD⊥x轴 于点 D，已知 sin∠DBC=55，OC:CD=3:1．
（1）求 y1 和 y2 的解析式；
（2）连接 OA，OB，求 △AOB 的面积．

23. 沙坪坝区政府决定从 2014 年 11 月起到 2016 年年底，两年的时间创建成为国家卫生城区，辖区内企业的污水处理通常有两种方式，一种是输送到污水厂进行集中处理，另一种是通过企业的自身设备进行处理，某企业每月的污水量均为 2500 吨，数量巨大需要两种处理方式同时进行．由于企业自身设备老化等问题，2015 年每月自身处理污水量 y（吨）与月份 x（x 取整数）之间满足的函数关系式为 y=2500−100x，该企业自身处理每吨污水的成本为 4 元，其余部分由污水厂统一处理，污水厂收取企业每吨污水处理费 10 元．
（1）该企业 2015 年哪几个月用于污水处理的费用不超过 12000 元?
（2）2016 年以来，由于该企业自建污水处理设备的全面运行，该企业决定扩大产能并将所有污水全部自身处理，估计扩大产能后 2016 年每月的污水量都将在 2015 年每月的基础上增加 a%，同时每吨污水处理的费用将在每吨 4 元的基础上增加 5a−30%，为鼓励节能降耗，减轻企业负担，财政对企业处理污水的费用进行 50% 的补助，若该企业每月的污水处理费用为 8437.5 元，请计算出 a 的值．

24. 在正方形 ABCD 中，BD 为对角线，
（1）如图 1，E，P 为直线 BC 上两点，连接 DP，DE，若点 E 为 BC 中点，BC=2，当 ∠DPC=∠EDC 时，求 △PED 的面积；
（2）如图 2，E 在 BD 上，且 ∠ECD=15∘，过点 C 作 CP⊥CE 交 DB 延长线于点 P，在 CP 上取点 F，连接 EF，延长 EC 至点 G 使 CG=CF，在 CP 上取点 H，连接 GH 使 GH=EF．求证：2DE=PH．

25. 如果关于 x 的一元二次方程 a2x+bx+c=0 有 2 个实数根，且其中一个实数根是另一个实数根的 3 倍，则称该方程为“立根方程”．
（1）方程 x2−4x+3=0 立根方程，方程 x2−2x−3=0 立根方程；（请填“是”或“不是”）
（2）请证明：当点 m,n 在反比例函数 y=3x 上时，一元二次方程 mx2+4x+n=0 是立根方程；
（3）若方程 ax2+bx+c=0 是立根方程，且两点 Pp+p2+1,q，Q−p2+5+q,q 均在二次函数 y=ax2+bx+c 上，请求出方程 ax2+bx+c=0 的两个根．

26. 如图，抛物线 y=−12x2+92x+5 与 x 轴交于点 A，点 B，与 y 轴交于点 D，在 y 轴负半轴有一点 E，使得 ∠EBO=∠DBO，第一象限抛物线上有一点 C，与点 D 关于对称轴对称．
（1）求直线 BE 解析式．
（2）在线段 BE，AB 上各有一动点 M，N，当 AM+MN 最小时，过点 M 作 y 轴的平行线，与抛物线交于点 P，求点 P 的坐标．
（3）如图 2，分别连接 BD，OC，一动点 Q 从点 O 出发，以每秒 1 个单位的速度向终点 B 运动，过点 Q 作 QH⊥x轴，与直线 OC 交于点 H，延长 QH 至点 F，使 FH=QH，以 QF 为斜边，在 QF 右侧作等腰直角三角形 QFK；同时另一动点 G 从点 B 出发，以每秒 2 个单位的速度向终点 O 运动，过点 G 作 GI⊥x轴，与直线 BD 交于点 I，延长 GI 至点 J，使 IJ=GI，以 GJ 为斜边，在 GJ 左侧作等腰直角三角形 GJR．已知一个动点停止运动，另一动点也随之停止运动，请问当点 Q 运动多少秒时，两个等腰直角三角形分别有一边恰好落在同一直线上?
答案
第一部分
1. B
2. B
3. D
4. C
5. A
6. D
7. C
8. C
9. A
10. C
11. A
12. B
第二部分
13. 7.14×108
14. 2−4
15. 94π
16. 16
17. 4511
18. 3−1
第三部分
19. ∵ 四边形 ABCD 是平行四边形，
∴ AD∥BC，
∴ ∠ODQ=∠OBP，
∵ O 是 BD 的中点，
∴ OB=OD，
在 △BOP 和 △DOQ 中，
∠OBP=∠ODQ,OB=OD,∠BOP=∠DOQ,
∴ △BOP≌△DOQ，
∴ OP=OQ．
20. （1） 0.36；100
（2） 因为 0.36+0.28×1200=768（名），
所以高三年级 1200 名学生中，胆汁型和多血质的约有 768 名．
21. （1） 原式=x2+4xy+4y2−x2−4y2=x2+4xy+4y2−x2+4y2=4xy+8y2.
（2） 原式=xx+3x−3÷2x−6−x−3−x2+9x+3x−3=xx+3x−3⋅x+3x−3x1−x=11−x.
22. （1） y1=k1x+6 与 y 轴的交点 E 的坐标为 0,6，
∴ OE=6，
∵ BD⊥x轴，
∴ OE∥BD，
∴ BDOE=CDOC=13，
∴ BD=2，
∵ sin∠DBC=55，
∴ 设 CD=5x，则 BC=5x，由勾股定理得，5x2=5x2+4，解得，x=55，则 CD=5x=1，则 BC=5x=5，
∴ 点 B 的坐标为 4,−2，
∴ −2=k1×4+6，解得，k1=−2，则 y1=−2x+6，y2=−8x；
（2） y=−8x,y=−2x+6,
解得，x1=−1,y1=8,x2=4,y2=−2,
∴ A−1,8，B4,−2，则 △AOB 的面积为 12×3×8+12×3×2=15．
23. （1） 根据题意得：
42500−100x+102500−2500−100x≤12000.
整理得：
600x+10000≤12000.
解得：
x≤103.∵
x 为正整数，
∴ x=1,2,3．
∴ 该企业 2015 年一、二、三月用于污水处理的费用不超过 12000 元．
（2） 根据题意得：
25001+a%×41+5a−30%=8437.5×2.
整理得：
a2+90a−4375=0.
解得：
a=35或a=−125舍去.
答：若该企业每月的污水处理费用为 8437.5 元，a 的值为 35．
24. （1） ∵ 四边形 ABCD 是正方形，
∴CD=BC=2，∠DCB=90∘，
∵ 点 E 为 BC 中点，
∴EC=1，
∵∠DPC=∠EDC，∠DCE=∠DCP，
∴△ECD∽△DCP，
∴DCCP=ECDC，
∴2PC=12，
∴PC=4，PE=3，
∴S△PDE=12⋅PE⋅DC=12×3×2=3.
（2） 如图，连接 BH．
∵CE⊥PC，
∴∠ECF=∠HCG=90∘，
在 △ECF 和 △HCG 中，
EC=CH,∠ECF=∠HCG,CF=CG,
∴△ECF≌△HCG，
∴EC=HC，
∵∠HCE=∠BCD=90∘，
∴∠ECD=∠BCH=15∘，
∵∠DBC=∠BCP+∠P=45∘，
∴∠P=30∘，
在 △BCH 和 △DCE 中，
BC=CD,∠BCH=∠ECD,CH=CE,
∴△BCH≌△DCE，
∴DE=BH，∠CBH=∠CDE=45∘，
∴∠DBH=∠DBC+∠CBH=90∘，
∴∠PBH=90∘，
∴PH=2BH，
∴PH=2DE．
25. （1） 是；不是
（2） ∵ 点 m,n 在反比例函数 y=3x 的图象上，
∴n=3m．
∵ mx2+4x+n=0，
∴ mx2+4x+3m=0，
解方程 mx2+4mx+3=0，
得：x1=−3m，x2=−1m，
∴ x1=3x2，
∴ 当点 m,n 在反比例函数 y=3x 上时，一元二次方程 mx2+4x+n=0 是立根方程．
（3） ∵ 方程 ax2+bx+c=0 是立根方程，
∴ 设 x1=3x2，
∵ 两点 Pp+p2+1,q，Q−p2+5+q,q 都在抛物线 y=ax2+bx+c 上，
∴ 抛物线的对称轴为直线 x=p+p2+1−p2+5+q2=6+p+q2，
∴ x1+x2=6+p+q，
∴ 3x2+x2=6+p+q，
∴ x2=6+p+q4，
∴ x1=3x2=18+3p+3q4．
∴ 方程 ax2+bx+c=0 的两个根为：x1=18+3p+3q4，x2=6+p+q4．
26. （1） 对于抛物线 y=−12x2+92x+5，令 x=0 得 y=5，令 y=0 得 −12x2+92x+5=0，解得 x=−1 或 x=10，
∴ D0,5，A−1,0，B10,0，
在 △BOD 和 △BOE 中，
∠DBO=∠EBO,BO=BO,∠BOD=∠BOE,
∴ △BOD≌△BOE，
∴OD=OE，
∴E0,−5，
设直线 BE 的解析式为 y=kx+b，则有 b=−5,10k+b=0, 解得 k=12,b=−5.
∴ 直线 BE 的解析式为 y=12x−5．
（2） 如图 1，作点 A 关于直线 BE 的对称点 Aʹ，连接 AAʹ 交 BE 于 Kʹ，交 y 轴于 T，作 AʹN⊥AB 于 N 交 BE 于 M，
此时 AM+MN 的值最小，
易得 ∠OAT=∠OEB，
∵ tan∠OEB=OBOE=2，
∴ tan∠OAT=2，
∵ OA=1，
∴ OT=2，T0,−2．
由 A−1,0，T0,−2，同直线 BE 的解析式的求法可得：
直线 AAʹ 的解析式为 y=−2x−2，
由 y=−2x−2,y=12x−5 解得 x=65,y=−225.
∴Kʹ65,−225，
∵ 点 A 和点 Aʹ 关于直线 BE 对称，
∴ Aʹ175,−445，
∴ 点 P 的横坐标为 175．
当 x=175 时，Py=−12×1752+92×175+5=36325，
∴ 点 P 坐标为 175,36325．
（3） 如图 2，延长 FK 交 x 轴于点 Eʹ，延长 JR 交 x 轴于点 Pʹ．
由题意可得 C9,5，
∴ 直线 OC 的解析式为 y=59x，
∵ B10,0，D0,5，
∴ 直线 BD 的解析式为 y=−12x+5．
由题意得 OQ=t，BG=2t，
∴ HQ=59t，IG=t，
∵ △FKQ 是等腰直角三角形，QH⊥x轴，
∴ ∠F=∠FEʹQ=45∘，QEʹ=QF=109t，
∵ △RJG 为等腰直角三角形，
∴ PʹG=JG=2t，
①当边 FK，边 RG 在同一直线上时，t+109t+2t=10，解得 t=9037，
②当边 QK，边 RJ 在同一直线上时，t+4t=10，解得 t=2，
③当边 FQ，边 JG 在同一直线上时，t+2t=10，解得 t=103，
综上所述，当点 Q 运动 9037 秒或 2 秒或 103 秒时，两个等腰直角三角形分别有一边恰好落在同一直线上．