2018年杭州市江干区中考一模数学试卷

这是一份2018年杭州市江干区中考一模数学试卷，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. 如图所示，直线 a，b 被直线 c 所截，∠1 的同位角是
A. ∠2B. ∠3C. ∠4D. ∠5

2. 实数 a，b，c，d 在数轴上的对应点的位置如图所示，则正确的结论是
A. b>−1B. ad>0
C. a>dD. b+c>0

3. 已知扇形的圆心角为 30∘，面积为 3π cm2，则扇形的半径为
A. 6 cmB. 12 cmC. 18 cmD. 36 cm

4. 如图是根据某班 40 名同学一周的体育锻炼情况绘制的统计图，该班 40 名同学一周参加体育锻炼时间的中位数，众数分别是
A. 10.5，16B. 8.5，16C. 8.5，8D. 9，8

5. 将多项式 4x2+1 再加上一项，使它能分解因式成 a+b2 的形式，以下是四位学生所加的项，其中错误的是
A. 2xB. −4xC. 4x4D. 4x

6. 如图，圆 O 是 △ABC 的内切圆，分别切 BA，BC，AC 于点 E，F，D，点 P 在弧 DE 上，如果 ∠EPF=70∘，那么 ∠B=
A. 40∘B. 50∘C. 60∘D. 70∘

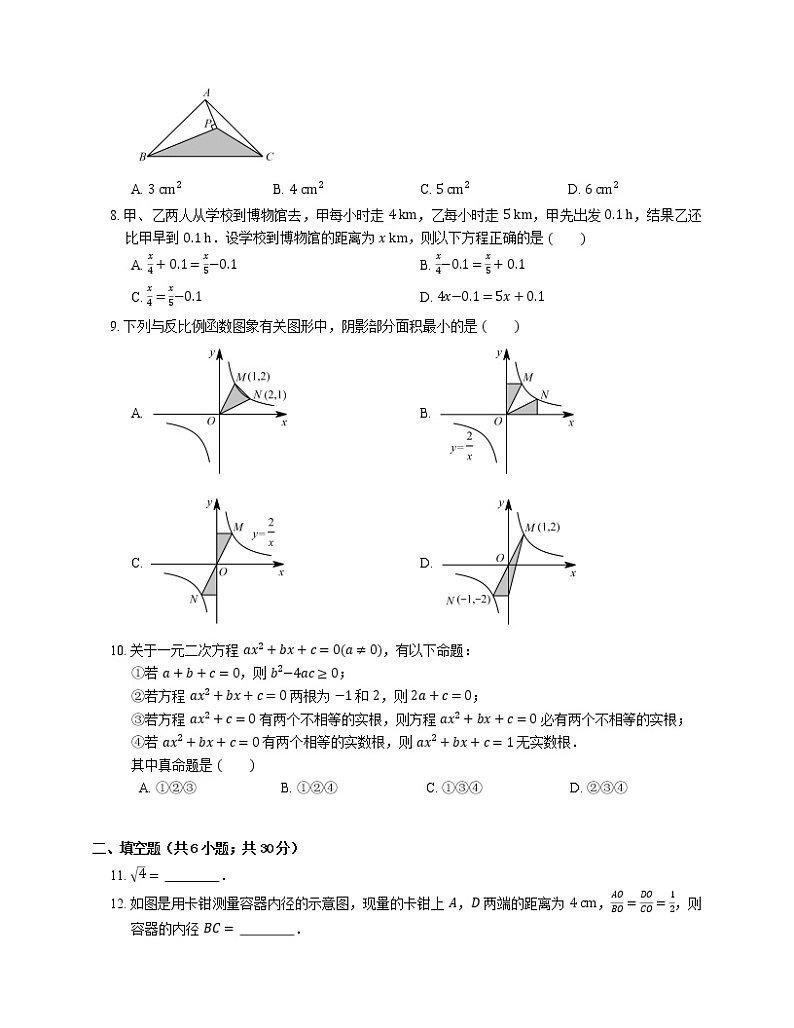
7. 如图，△ABC 的面积为 8 cm2，AP 垂直 ∠B 的平分线 BP 于 P，则 △PBC 的面积为
A. 3 cm2B. 4 cm2C. 5 cm2D. 6 cm2

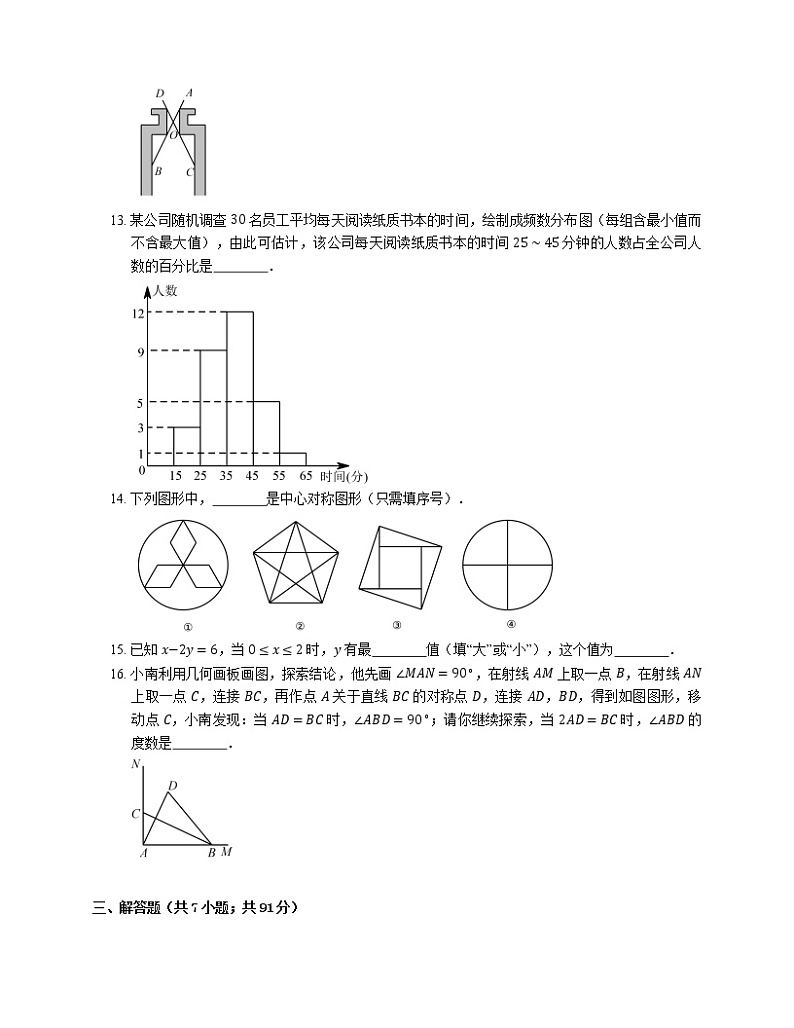
8. 甲、乙两人从学校到博物馆去，甲每小时走 4 km，乙每小时走 5 km，甲先出发 0.1 h，结果乙还比甲早到 0.1 h．设学校到博物馆的距离为 x km，则以下方程正确的是
A. x4+0.1=x5−0.1B. x4−0.1=x5+0.1
C. x4=x5−0.1D. 4x−0.1=5x+0.1

9. 下列与反比例函数图象有关图形中，阴影部分面积最小的是
A. B.
C. D.

10. 关于一元二次方程 ax2+bx+c=0a≠0，有以下命题：
①若 a+b+c=0，则 b2−4ac≥0；
②若方程 ax2+bx+c=0 两根为 −1 和 2，则 2a+c=0；
③若方程 ax2+c=0 有两个不相等的实根，则方程 ax2+bx+c=0 必有两个不相等的实根；
④若 ax2+bx+c=0 有两个相等的实数根，则 ax2+bx+c=1 无实数根．
其中真命题是
A. ①②③B. ①②④C. ①③④D. ②③④

二、填空题（共6小题；共30分）
11. 4= ．

12. 如图是用卡钳测量容器内径的示意图，现量的卡钳上 A，D 两端的距离为 4 cm，AOBO=DOCO=12，则容器的内径 BC= ．

13. 某公司随机调查 30 名员工平均每天阅读纸质书本的时间，绘制成频数分布图（每组含最小值而不含最大值），由此可估计，该公司每天阅读纸质书本的时间 25∼45 分钟的人数占全公司人数的百分比是 ．

14. 下列图形中， 是中心对称图形（只需填序号）．

15. 已知 x−2y=6，当 0≤x≤2 时，y 有最 值（填“大”或“小”），这个值为 ．

16. 小南利用几何画板画图，探索结论，他先画 ∠MAN=90∘，在射线 AM 上取一点 B，在射线 AN 上取一点 C，连接 BC，再作点 A 关于直线 BC 的对称点 D，连接 AD，BD，得到如图图形，移动点 C，小南发现：当 AD=BC 时，∠ABD=90∘；请你继续探索，当 2AD=BC 时，∠ABD 的度数是 ．

三、解答题（共7小题；共91分）
17. 计算 x2x+2−x+2，乐乐同学的计算过程如下：x2x+2−x+2=x2x+2−x+2x−2x+2=x2x+2−x2+4x+4x+2=−4x+4x+2，请判断计算过程是否正确，若不正确，请写出正确的计算过程．

18. 某校为了解八年级学生一学期参加公益活动的时间情况，抽取 50 名八年级学生为样本进行调查，按参加公益活动的时间 t（单位：小时），将样本分成五类：A类（0≤t≤2），B类（28），绘制成尚不完整的条形统计图．
（1）样本中，E类学生有 人，请补全条形统计图；
（2）该校八年级共 600 名学生，求八年级参加公益活动时间 6（3）从样本中选取参加公益活动时间在 0≤t≤4 的 2 人做志愿者，求这 2 人参加公益活动时间都在 2
19. 如图，在 △ABC 中，AD，DE 是中线，它们相交于点 F，EG∥BC，交 AD 于点 G．
（1）找出图中的一对相似三角形，并说明理由；
（2）求 AG 与 DF 的比．

20. 2017∼2018 赛季中国男子篮球职业联赛季后赛正如火如荼的进行．在浙江广厦队与深圳马可波罗队的一场比赛中，广厦队员福特森在距篮下 4 米处跳起投篮，篮球准确落入篮圈，已知篮球运行的路线是抛物线，当球运行的水平距离为 2.5 m 时，达到最大高度 3.5 m，篮圈中心到地面的距离为 3.05 m．
（1）建立如图所示的直角坐标系，求抛物线的函数表达式；
（2）已知福特森身高 1.8 m，在这次跳投中，球在头顶上方 0.25 m 处出手，问：球出手时，他跳离地面的高度是多少?

21. △ABC 中，点 P 是边 AC 上的一个动点，过点 P 作直线 MN∥BC，设 MN 交 ∠BCA 的平行线于点 E，交 ∠BCA 的外角平分线于点 F．
（1）求证：PE=PF；
（2）点 P 运动到 AC 边上某个位置时，四边形 AECF 是菱形，此时：
① ∠BCA= 度，请说明理由．
②已知 PA:BC=1:23，求 sin∠B 的值．

22. 二次函数 y=x2+mx+n 的图象经过点 A−1,a，B3,a，且最低点的纵坐标为 −4．
（1）求 m，n 和 a 的值；
（2）若直线 y=kx+2 经过点 A，求 k 的值；
（3）记（1）中的二次函数图象在点 A，B 之间的部分图象为 G（包含 A，B 两点），若直线 y=kx+2 与 G 有公共点，请结合图象探索实数 k 的取值范围．（注意：请在答题卡的直角坐标系中画出解题时使用的函数草图）

23. 有一个正方形 ABCD 和一个以 O 为顶点直角，移动这个直角，使两直角边分别与直线 BC，CD 交于 M，N．
（1）如图 1，若顶点 O 与点 A 重合，则线段 OM 与 ON 的数量关系是 ；
（2）如图 2，若顶点 O 在正方形的中心（即两对角线的交点），则（1）中的结论是否仍然成立?请说明理由．
（3）如图 3，若顶点 O 在正方形的内部（含边界）的任意位置．
①此时，（1）中的结论是否仍然成立?请说明理由（提示：若成立，请写出证明过程；若不成立，请举反例说明）；
②已知 AB=4，移动顶点 O，使 OM=ON 且四边形的面积为 1，请探究点 O 的位置（提示：可以用“点 O 在 ×× 线上，且到点 × 的距离是 ××”表示点 O 的位置）．
答案
第一部分
1. C
2. C
3. A
4. D
5. A
6. A
7. B
8. B
9. A
10. A
第二部分
11. 2
12. 8 cm
13. 70%
14. ③④
15. 小，−3
16. 30∘ 或 150∘
【解析】分两种情况：
如图，当 AB>AC 时，取 BC 的中点 E，连接 AE，DE，
则 AE=DE=12BC，即 BC=2AE=2DE，
又 ∵BC=2AD，
∴AD=AE=DE，
∴∠AED=60∘，
又 ∵BC 垂直平分 AD，
∴∠AEC=30∘，
又 ∵BE=AE，
∴∠ABC=12∠AEC=15∘，
∴∠ABD=2∠ABC=30∘；
当 AB又 ∵∠BAC=∠BDC=90∘，
∴∠ABD=150∘．
第三部分
17. 乐乐计算错误；
原式=x2x+2−x−2x+2x+2=x2x+2−x2−4x+2=4x+2.
18. （1） 5
【解析】E类：50−2−3−22−18=5（人），统计图略．
（2） D类：18÷50×600=216．
（3） 方法不限，0.3．
19. （1） 略．
（2） AG:DF=3:2．
20. （1） 由题意，抛物线的顶点坐标为 0,3.5，
∴ 设抛物线的表达式为 y=ax2+3.5．
由图知图象过以下点：1.5,3.05．
∴2.25a+3.5=3.05，解得：a=−0.2，
∴ 抛物线的表达式为 y=−0.2x2+3.5．
（2） 设球出手时，篮球离地面的高度为 h m，此时 x=−2.5，
∴h=−0.2x2+3.5=−0.2−2.52+3.5=2.25，
∴ 球出手时，跳离地面的高度是 2.25−1.80−0.25=0.2．
答：球出手时，他跳离地面的高度为 0.2 m．
21. （1） 因为 CE 平分 ∠BCA，∠BCE=∠ECP，
又因为 MN∥BC，
所以 ∠BCE=∠CEP，
所以 ∠ECP=∠CEP，
所以 PE=PC，同理 PF=PC，
所以 PE=PF．
（2） ① 90
若四边形 AECF 是菱形，则 AC⊥EF，AC=2AP．
因为 EF∥BC，
所以 AC⊥BC，
所以 △ABC 是直角三角形，且 ∠ACB=90∘．
② tan∠B=ACBC=223=33，
所以 ∠B=30∘，sin∠B=12．
22. （1） ∵ 抛物线 y=x2+mx+n 过点 A−1,a，B3,a，
∴ 抛物线的对称轴 x=1．
∵ 抛物线最低点的纵坐标为 −4，
∴ 抛物线的顶点是 1,−4．
∴ 抛物线的表达式是 y=x−12−4，即 y=x2−2x−3．m=−2，n=−3，
把 A−1,a 代入抛物线表达式 y=x2−2x−3，求得 a=0．
（2） 把 A−1,0 的坐标代入 y=kx+2，得 k=2．
（3） 画草图，
当 y=kx+2 经过点 B3,0 时，0=3k+2，k=−23，
∴ 当 k≤−23 时，直线 y=kx+2 与 G 有公共点，
当 y=kx+2 经过点 A−1,0 时，0=−k+2，k=2，
∴ 当 k≥2 时，直线 y=kx+2 与 G 有公共点，
综上所述，当 k≤−23 或 k≥2 时，直线 y=kx+2 与 G 有公共点．
23. （1） OM=ON
（2） 结论成立，理由略．
（3） ①结论不成立．
反例：如图，当点 O 是 AB 的中点时，若点 N 是 CD 的中点，
则点 M 和点 B 重合，此时 OM=0.5ON；
②结论：点 O 在线段 AC 上，距离点 C 为 2 的位置，
理由：如图，作 OP⊥BC 于 P，OQ⊥CD 于 Q，
先证 △OPM≌△OQN，得 OP=OQ，可知点 O 在 ∠C 的平分线上；
四边形 OMCN 的面积为 1，即四边形 OPCQ 的面积为 1，所以 PC=1，OC=2．